Coulomb's Law

Coulomb's Law

AU : May-2000,05,08,13,14,16, Dec.-02,05,09,14,16.17

• The study of electrostatics starts with the study of the results of the experiements performed by an engineer from the French Army Engineers, Colonel Charles Coulomb. The experiments are related to the force exerted between the two point charges, which are placed near each other. The force exerted is due to the electric fields produced by the point charges.

• A point charge means that electric charge which is spreaded on a surface or space whose geometrical dimensions are very very small compared to the other dimensions, in which the effect of its electric field is to be studied. Thus a point charge has a location but not the dimensions. A charge can be a positive or negative. A charge is actually the deficiency or excess of electrons in the atoms of a particle. An electron possesses a negative charge. So the deficiency of an electron produces positive charge while excess of an electron produces negative charge. The charge is measured in Coulombs (C). The smallest possible charge is that corresponding to the charge on one electron which is 1.602 × 10^-19 C. Hence one Coulomb of charge is defined as the charge possessed by (1/1.602 × 10^-19) i.      e. 6 × 10¹⁸ number of electrons. There can be an isolated positive or negative charge which exerts force on other charge placed in its vicinity. It is well known that the like charges repel while unlike charges attract each other. The Coulomb's law formulated in 1785 is related to such a force exerted by one charge on the other.

 

1. Statement of Coulomb's Law

• The Coulomb's law states that force between the two point charges Q₁ and Q₂,

1. Acts along the line joining the two point charges.

2. Is directly proportional to the product (Q₁Q₂) of the two charges.

3. Is inversely proportional to the square of the distance between them.

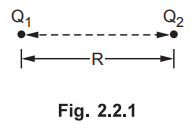
• Consider the two point charges Q₁ and Q₂ as shown in the Fig. 2.2.1, separated by the distance R. The charge Q₁ exerts a force on Q₂ while Q₂ also exerts a force on Q₁. The force acts along the line joining Q₁ and Q₂. The force exerted between them is repulsive if the charges are of same polarity while it is attractive if the charges are of different polarity.

• Mathematically the force F between the charges can be expressed as,

F ∞ Q₁Q₂ /R₂ .....(2.2.1)

Where         Q₁Q₂ = Product of the two charges

R = Distance between the two charges

• The Coulomb's law also states that this force depends on the medium in which the point charges are located. The effect of medium is introduced in the equation of force as a constant of proportionality denoted as k.

F = Q1Q₂/R₂ .....(2.2.2)

Where         k = Constant of proportionality

 

a. Constant of Proportionality (k)

• The constant of proportionality takes into account the effect of medium, in which charges are located. In the International System of Units (SI), the charges Q₁ and Q₂ are expressed in Coulombs (C), the distance R in metres (m) and the force F in newtons (N). Then to satisfy Coulomb's law, the constant of proportionality is defined as,

K= 1/4πε... (2.2.3)

where          ε = Permittivity of the medium in which charges are located

• The emits of ε are farads/metre (F/m).

• In general ε is expressed as,

ε = ε₀ ε_r .....(2.2.4)

where          ε₀ = Permittivity of the free space or vacuum

ε_r = Relative permittivity or dielectric constant of the medium with respect to free space

ε = Absolute permittivity

• For the free space or vacuum, the permittivity ε_r = 1, hence

ε = ε₀

F = 1/4πε0 Q₁Q₂/R² ....(2.2.5)

• The value of permittivity of free space e 0 is,

• Hence the Coulomb's law can be expressed as,

F = Q₁Q₂/4πε₀R²

• This is the force between the two point charges located in free space or vacuum.

Key Point : As Q is measured in Coulomb, R in metre and F in newton, the units of ε₀ are,

But C²/N - m = Farad which is practical unit of capacitance

Unit of ε₀ = F/m

 

2. Vector Form of Coulomb's Law

• The force exerted between the two point charges has a fixed direction which is a straight line joining the two charges. Hence the force exerted between the two charges can be expressed in a vector form.

• Consider the two point charges Q₁ and Q₂ located at the points having position vectors  as shown in the Fig. 2.2.2.

• Then the force exerted by Q₁ on Q₂ acts along the direction 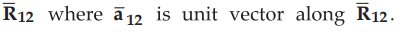 Hence the force in the vector form can be expressed as

whereDistance between the two charges The following observations are important :

1. The force exerted by the two charges on each other is equal but opposite in direction, hence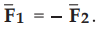 

2. The like charges repel each other while the unlike charges attract each other. This is shown in the Fig. 2.2.3. These are experiement conclusions though not reflected in the mathematical expression.

3. It is necessary that the two charges are the point charges and stationary in nature.

4.The two point charges may be positive or negative. Hence their signs must be considered while using equation (2.2.9) to calculate the force exerted.

5. The Coulomb's law is linear which shows that if any one charge is increased 'n' times then the force exerted also increass by n times.

 

3. Principle of Superposition

• If there are more than two point charges, then each will exert force on the other, then the net force on any charge can be obtained by the principle of superposition. Consider a point charge Q surrounded by three other point charges Q₁, Q₂ and Q₃, as shown in the Fig. 2.2.4.

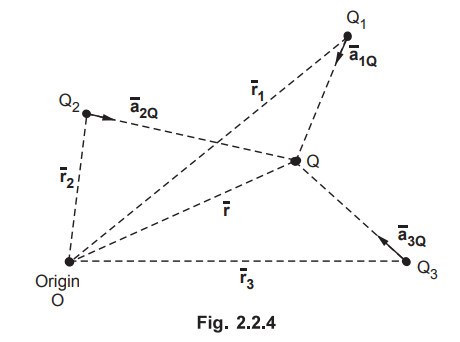
• The total force on Q in such a case is vector sum of all the forces exerted on Q due to each of the other point charges Q₁, Q₂ and Q₃. Consider force exerted on Q due to Q₁. At this time, according to principle of superposition effects of Q₂ and Q₃ are to be suppressed.

 

 

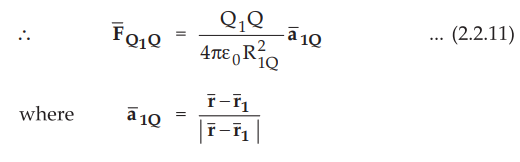
• Similarly force exerted due to Q₂ on Q is,

• In general if there are n other charges then force exerted on Q due to all other n charges is,

 

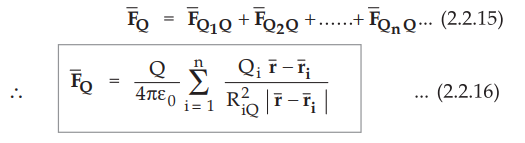
4. Steps to Solve Problems on Coulomb’s Law

Step 1 : Obtain the position vectors of the points where the charges are located.

Step 2 : Obtain the unit vector along the straight line joining the charges. The direction is towards the charge on which the force exerted is to be calculated.

Step 3 : Using Coulomb's law, express the force exerted in the vector form.

Step 4 : If there are more charges, repeat steps 1 to 3 for each charge exerting a force on the charge under consideration.

Step 5 : Using the principle of superposition, the vector sum of all the forces calculated earlier is the resultant force, exerted on the charge under consideration.

 

Ex. 2.2.1 A Charge 20 µC is located at A(-6,4,-7) and another charge 50 µC is at B(5,8,-2) in free space. If distance are given in meters, determine the vector force exerted by the first charge on the second one. AU: Dec.-17, Marks 4

Sol. : The charges are shown in the Fig. 2.2.5.

= 41.223 mN

 

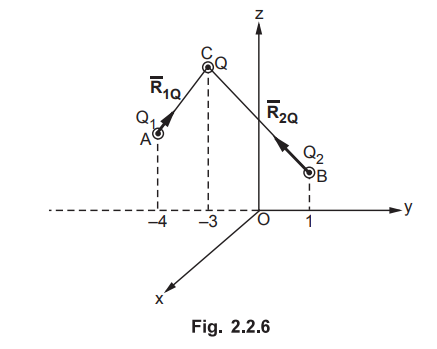
Ex. 2.2.2 Q₁ and Q₂ are the point charges located at (0, -4, 3) and (0,1,1). If Q₁ is 2 nC, find Q₂ such that the force on a test charge at (0, -3,4) has no z component. Sol. : The charges are shown in the Fig. 2.2.6.

The position vectors of the points A, B and C are,

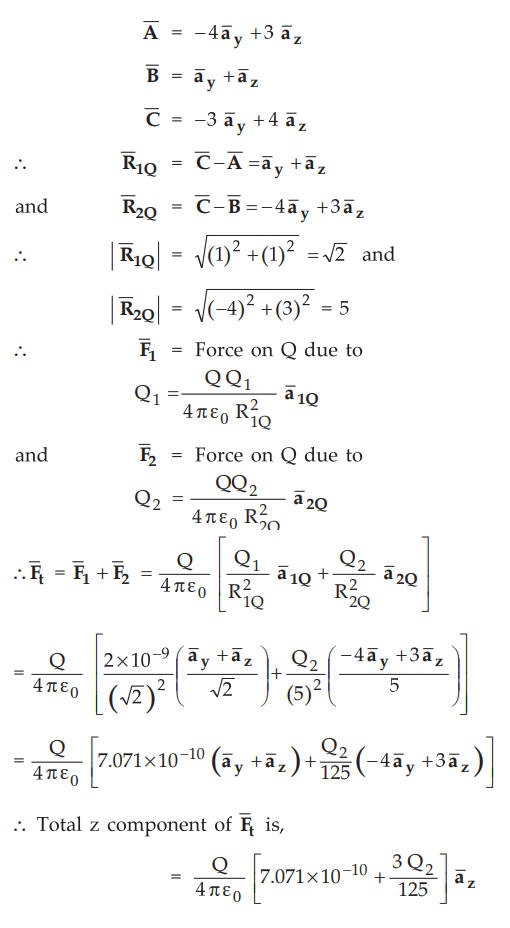
To have this component zero,

7.071 × 10^-10 + 3Q₂/125 = 0 as Q is test charge and cannot be zero.

Q₂ = 7.071 × 10^-10 × 125/3= - 29.462 nC

 

Ex. 2.2.3 Two small identical conducting spheres have charges of 2 nC and -1 nC respectively. When they are separated by 4 cm apart, find the magnitude of the force between them. If they are brought into contact and then again separated by 4 cm, find the force between them. AU : May-2000, 06

Sol. : Case 1 : Before the charges are brought into contact

Case 2 : The charges are brought into contact and then separated.

When charges are brought into contact, the charge distribution takes place due to transfer of charge. The transfer of charge continues till both the charges attain same value due to equal division of the two charges.

 Charge on each sphere = Q₁+ Q₂/2

(2 × l0^-9) + (-l × l0^-9)/2 = (2-1) × l0^-9/2 = 0.5 nC

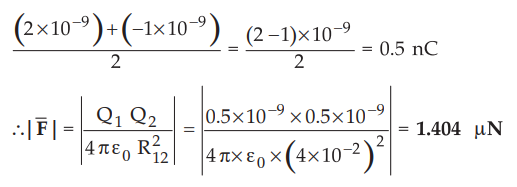
Note that initially before charges are brought together the force between them was attractive as charges are of opposite polarity. But when they are brought in contact and then separated, the force is repulsive in nature.

 

Ex. 2.2.4 A charge Q₁= 100 nC is located in vacuum at P₁(- 0.03, 0.01, 0.04) m. Find the force on Q₁ due to i) Q₂ = 120 µC at _P2 (0.03, 0.08, - 0.02) m ii) Q₃ = 120 µC at P₃ (- 0.09, - 0.06, 0.10) m iii) Q₂ and Q_3. AU : May-16, Marks 8

Sol. : The charges are shown in the Fig. 2.2.7

 

Ex. 2.2.5 Three concentrated charges of 0.25 µC are located at the vertices of an equilateral triangle of 10 cm side. Find the magnitude and direction of the force on one charge due to other two charges.AU: Dec.-09, Marks 8

Sol. : The arrangement is shown in the Fig. 2.2.8.

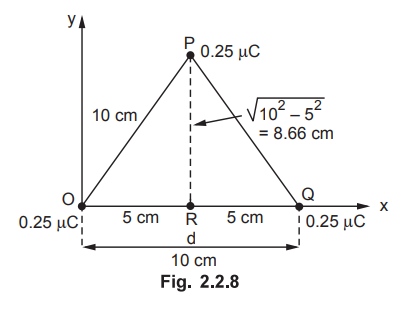
The co-ordinates of the vertices of triangle are,

Point O →(0, 0, 0)

Point Q →(0.1, 0, 0)

Point P →(0.05, 0.0866, 0).

Let us find the force on P due to the charges at O and Q.

 

Ex. 2.2.6 Four point charges of 10 µCeach are placed at the corners of square of side 1 m. Determine the value of the charge that is to be placed at the centre of the square so that this system of charges is brought to equilibrium. AU: May-14, Marks 8

Sol. : The square is shown in the Fig. 2.2.9 which is kept in x - y plane.

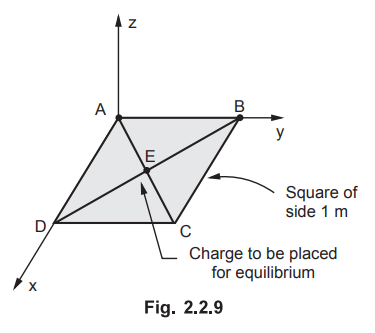
 The co-ordinates of various points are,

A(0, 0, 0), B(0, 1, 0), C(l, 1, 0), D(l, 0, 0), E(0.5, 0.5, 0)

To hold all the charges in equilibrium, the net force exerted on any of the charges due to other charges must be zero.

Let us find force exerted on the charge at A due to other charges.

 

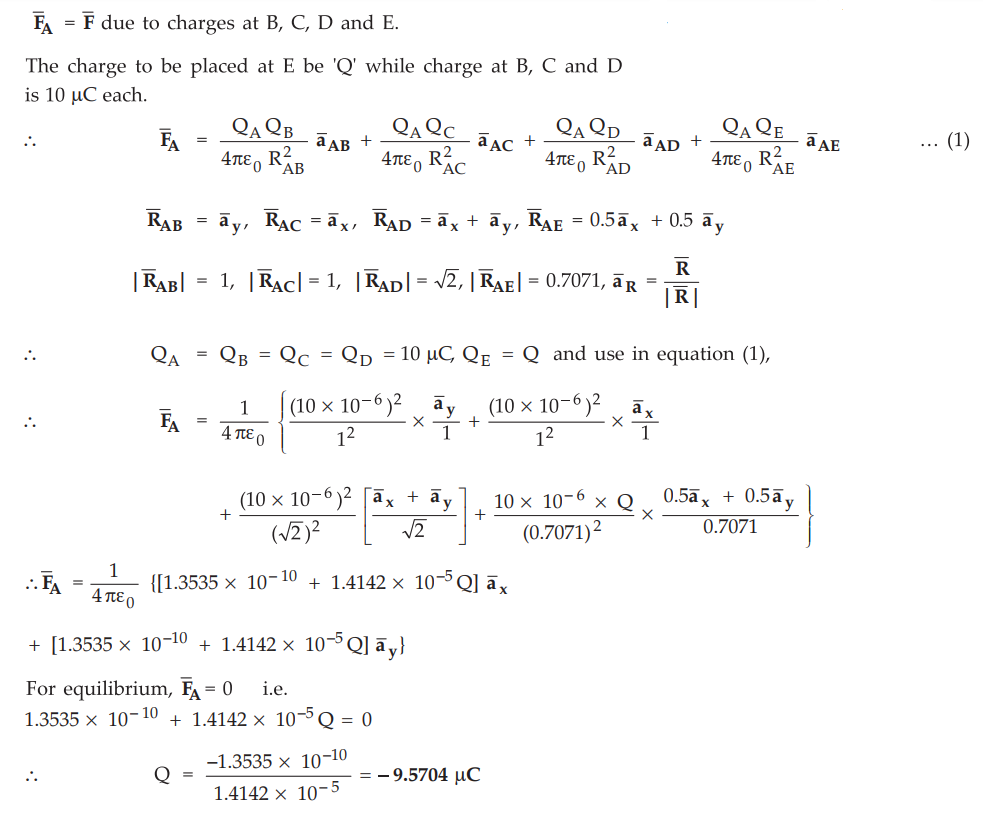
Ex. 2.2.7 Find the force on a charge Q₁ of 20 µC at (0, 1, 2) m due to Q₂ of 300 µC at (2, 0, 0)m. AU: Dec.-16 Marks 5

Sol. :

Examples for Practice

Ex. 2.2.8 A charge Q₂ = 10 µC is located in an air at P₂(-3, 1, 4) m. Find the force on Q₂ due to Q₁ = 33 µC located at P₁ (3, 8, - 2) m. 

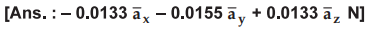
Ex.e 2.2.9 A point charge Q₁ = 300 µC is located at (1 - 1, - 3) m and experiences a force 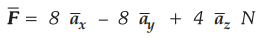 due to a point charge at (3, -3, -2) m. Find the other charge Q₂. 

[Ans.: - 40 µC]

Ex. 2.2.10 A is required to hold four equal point charges each in equilibrium at the corners of a square. Find the point charge which will do this, if placed at the centroid of the square. 

[Ans.: - 0.9571 Q C]

Ex. 2.2.11 Three point charges q₁ = 10^-6 C, q₂ = -10^-6 C and q₃ = 0.5 × 10-6 C are located in air at the corners of an equilateral triangle of 50 cm side. Determine the magnitude and direction of the force on q₃.

Review Questions

1. State and explain Coulomb's law and deduce the vector form of force equation between two point charges. 

AU : May-13, Dec.-14, Marks 6

2. Write a note on principle of superposition as applied to charge distribution. 

AU : May-05, 08, Dec.-02, 05, Marks 4