Covariance, correlation and regression: Example Solved Problems

Example 2.2.1

Calculate the correlation co-efficient for the following heights (in inches) of fathers X and their sons Y.

[A.U. N/D 2004, A/M 2015 (RP) R13]

Solution :

The correlation co-efficient of X and Y is given by,

r (X, Y) = Cov (X, Y) / σ_X. σ_Y = 3/ (2.121) (2.345) = 3 / 4.973 = 0.6032

Note: Correlation co-efficient is independent of change of origin and scale.

i.e., r (X, Y) = r (U, V) where U = X - ɑ / h ; V = Y - b / K

where a and b are some arbitrary constants usually the mid-values of the given data X and Y respectively.

 

Example 2.2.2

Find the rank correlation co-efficient from the following data:

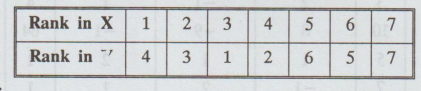
Solution :

Example 2.2.3

Ten participants were ranked according to their performance in a mustical test by the 3 Judges in the following data.

Using rank correlation method, discuss which pair of judges has the nearest approach to common likings of music.

Solution:

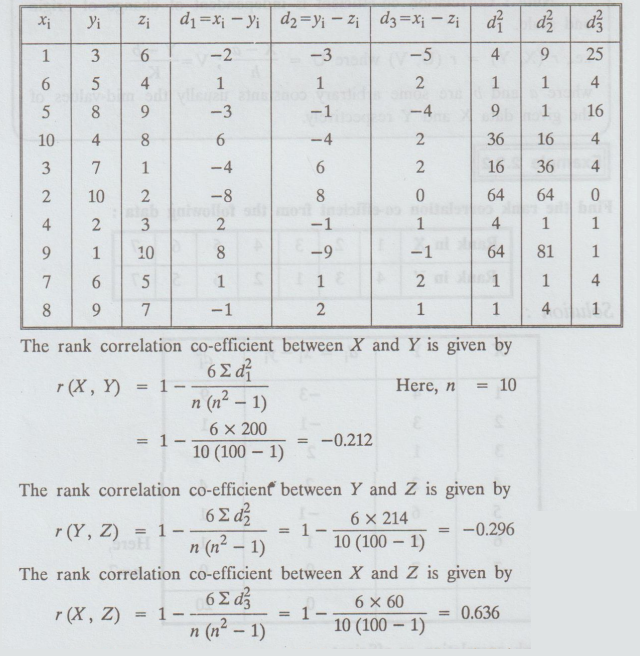
Since the rank correlation coefficient between X and Z is positive and maximum, we conclude that the pair of judges X and Z has the nearest approach to common liking in music.

 

Example 2.2.4

Obtain the rank correlation coefficient for the following data:

Solution :

In X series 75 is repeated twice which are in the positions 2nd and 3rd ranks. Therefore common ranks 2.5 (which is the average of 2 and 3) is to be given for each 75. Also in X series 64 is repeated thrice which are in the position 5th, 6th and 7th ranks.

Therefore common ranks 6 (which is the average of 5, 6 and 7) is to be given for each 64.

Similarly in Y series 68 is repeated twice which are in the positions 3rd and 4th ranks. Therefore common ranks 3.5 (which is the average of 3 and 4) is to be given for each 68.

Correction factors

In X series 75 is repeated twice

 

Example 2.2.5

The joint probability mass function of X and Y is given below.

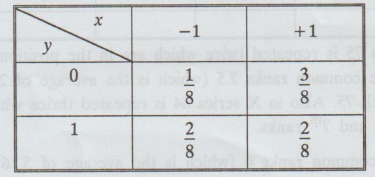
Find the correlation coefficient of (X, Y).

Solution :

 

Example 2.2.6

Let X and Y be discrete R.V's with probability function

f(x, y) = x+y / 21 x = 1,2,3; y = 1,2.

 [A.U N/D 2015 R13, CBT A/M 2011]

Find (i) Mean and Variance of X and Y.

(ii) Cov (X, Y)

(iii) Correlation of X and Y.

[A.U A/M 2019 (R17) PQT]

 

Example 2.2.7

Two random variables X and Y have the joint density

 [AU, N/D. 2004, M/J 2006, N/D 2010, Tvli A/M 2009, M/J 2010] [A.U. CBT M/J 2010] [A.U N/D 2011] [A.U A/M 2019 (R13) PQT]

Solution:

The marginal density function of X is,

 

Example 2.2.8

Suppose that the 2D RVs (X, Y) has the joint p.d.f.

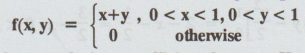Obtain the correlation co-efficient between X and Y.

Check whether X and Y are independent.

[AU, N/D, 2003, 2004] [A.U Tvli M/J 2010] [A.U A/M 2010] [A.U CBT N/D 2011] [A.U N/D 2017 (RP) R-13]

Solution: The marginal density function of X is given by,

 

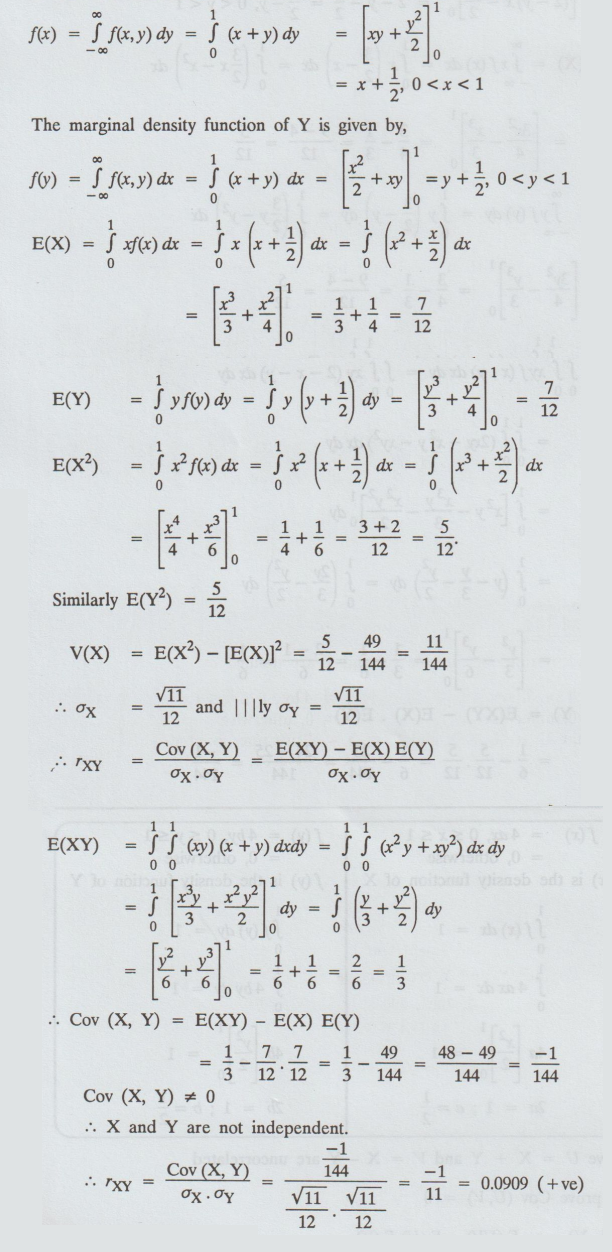
Example 2.2.9

Let X be a random variable with p.d.f f(x) = 1/2, -1 ≤ x ≤ 1 and let Y = X². Prove that, the correlation co-efficient between X and Y is zero.

Solution:

 

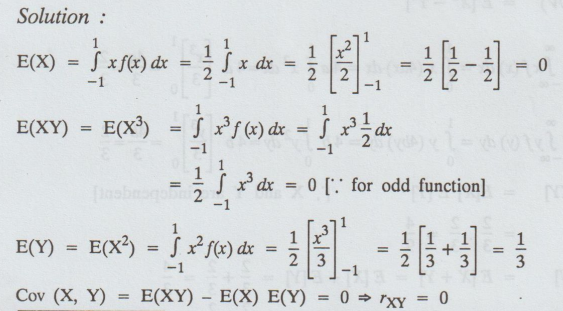
Example 2.2.10

Two independent random variables X and Y are defined by,

f(x) = 4 ax, 0 ≤ x ≤ 1

= 0, otherwise

f(y)= 4 by, 0 ≤ y ≤ 1

= 0, otherwise

Show that U = X + Y and V = X - Y are uncorrelated.

[AU A/M 2003, N/D 2012, M/J 2013]

Solution :

 

Example 2.2.11

If (X, Y) is a two-dimensional random variable uniformly distributed over the triangular region R bounded by y = 0, x = 3, and y = 4/3 x. Find the correlation coefficient r_xy.

[A.U.]

Sol. (X, Y) is uniformly distributed, f(x, y) = K, constant (say)

To find the point of Xⁿ of x = 3 and y = 4 / 3^x

y = 4 / 3 x, where x = 3 ⇒ y = 4

f(x, y) is a pdf, we have

 

Example 2.2.12

Let X₁ and X₂ be two independent random variables with means 5 and 10 and standard deviations 2 and 3 respectively. Obtain r_UV where U = 3X₁ + 4X₂ and V = 3X₁ - X₂.  [A.U N/D 2019 (R17) PS]

Solution: