Critical Field Resistance in D.C. Shunt Generator

Critical Field Resistance in D.C. Shunt Generator

AU: Dec.-05

• Consider the magnetisation characteristics of a d.c. shunt generator shown in the Fig. 3.29.1.

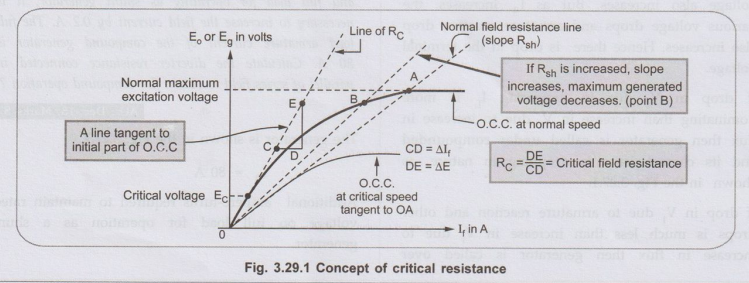
• The Fig. 3.29.1 shows that generator voltage builds in step till point A. This point is intersection of field resistance line with the Open Circuit Characteristics (O.C.C.). The voltage corresponding to point A is the maximum voltage it can generate. If the slope of field resistance line is reduced by decreasing thebuild will be higher than that corresponding to point A. Similarly if the slope of field resistance line is increased by increasing the field resistance, the maximum voltage generator can build will be less than that corresponding to point A i.e.corresponding to point B.

• If now the slope of the field resistance line is increased in such a way that it becomes tangential to the lower part of the open circuit characteristics. The voltage corresponding to this point is Ec. This voltage is just sufficient to drive the current through field resistance so that cumulative process of building the voltage starts. This value of field resistance is called the critical resistance denoted as Rc, of the shunt field circuit at given speed.

Key Point: If field circuit resistance is more than R_C at start then induced e.m.f. fail to drive current through field circuit and generator fails to excite at given speed.

Thus we can define critical resistance as that resistance of the field circuit at a given speed at which generator just excites and starts voltage building while beyond this value generator fails to excite.

The critical resistance is the slope of the critical resistance line.

ஃ    Rc = ΔΕ / ΔΙ_f  =  DE / CD = tan θ

• Similar to the critical resistance there is a concept of critical speed N_C. We know that E ∞ N. As speed decreases the induced e.m.f. decreases and we get O.C.C. below the O.C.C. at normal speed. If we go on reducing the speed, at a particular speed we will get O.C.C. just tangential to normal field resistance line.

Key Point: This speed at which the machine just excites for the given field circuit resistance is called the critical speed of a shunt generator denoted as N_C.

1. Practical Determination of R_C

• Generally data for plotting the open circuit characteristics is given. Plot the characteristics is given. Plot the characteristics on the graph paper to the scale.

• Draw the tangent, to the initial part of this O.C.C. then the slope of this line is the critical resistance for the speed at which the data is given.

Key Point: If speed changes, then the O.C.C. changes hence the value of R_C changes.

Now if Rc is asked at speed N₂, while data for O.C.C. is given at N₁. It is known that,

Key Point: Generate the data for O.C.C. at new speed and repeat the procedure to obtain Rc.

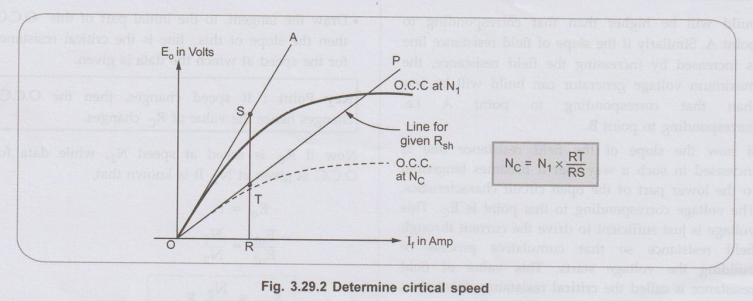
2. Critical Speed N_C

• It is known that as speed changes, the open circuit characteristics also changes, similarly for different shunt field resistances, the corresponding lines are also different.

Key Point: The speed for which the given field resistance acts as critical resistance is called the critical speed, denoted as N_C.

• Thus if the line is drawn representing given Rsh then O.C.C. drawn for such a speed to which this line is tangential to the initial portion, is nothing but the critical speed N_C.

Graphically critical speed can be obtained for given R_sh. The steps are,

1. Drawn O.C.C. for given speed N₁.

2. Draw a line tangential to this O.C.C. say OA.

3. Draw a line representing the given R_sh say OP.

4. Select any field current say point R.

5. Draw vertical line from R to intersect OA at S and OP at T.

6. Then the critical speed N_C is,

While RT /RS = N_C/ N₁ i.e N_C = N₁ RT / RS

Ex. 3.29.1 The following figures give the open circuit characteristic of a d.c. shunt generator running at 300 r.p.m.

Determine the voltage to which machine will excite if field circuit resistance is 40 ohm and run at 375 r.p.m.

i) What additional resistance would have to be inserted in the field circuit to reduce the voltage to 200 V at 375 r.p.m.

ii) Without additional resistance determine the load current supplied by the generator when its terminal voltage is 200 V. Ignore armature reaction and assume speed to be constant. Armature resistance is 0.4 ohm.

Sol.  For the shunt generator

Construct the new table for open circuit characteristics at N₂ = 375 r.p.m, using above relation.

The graph is shown in the Fig. 3.29.3.

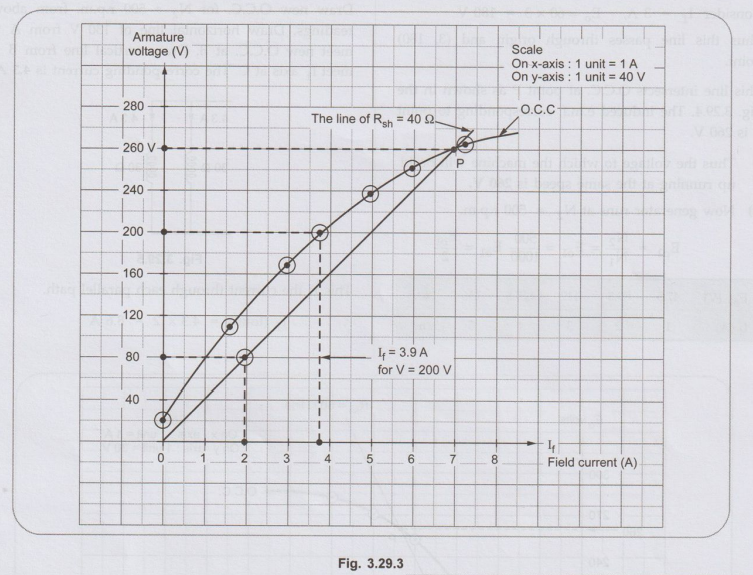
Draw the line corresponding to R_sh = 40 Ω . Το draw this line, consider the equation of line as y = mx which passes through origin and slope m which is nothing but R_sh

V = R_sh I_f …. For line of R_sh

So two point are, (0, 0) and (2, 80). From these points draw the straight line till it intersects O.C.C. at point P as shown. The voltage corresponding to point P is 260 V. Thus machine will excite to 260 V if

R_sh = 40 Ω and speed 375 r.p.m.

i. To have V = 200 V, find I_f from the graph which is, I_f = 3.9 A

Ex. 3.29.2 A shunt generator running at a speed of 1000 r.p.m. gave the following magnetization curve:

If the field circuit resistance is 60 Ω, determine

i)The voltage to which the machine will build up running at the same speed.

ii) The value of the field regulating resistance if the machine is to build up to 130 V, when its field coils are grouped into two parallel circuits and generator is run at 500 r.p.m. AU: Dec.-05, Marks 16

Sol. : Draw the open circuit characteristics on the graph paper from the given data.

Draw the line corresponding to Rsh = 60 Ω For this, consider an equation of line y = mx, passing through the origin.

Consider If = 3 A Eo = 60 × 3 = 180 V

Thus this line passes through origin and (3,180) point

This line intersects O.C.C. at point P as shown in the Fig.3.29.4. The induced e.m.f. corresponding to point P is 260 V

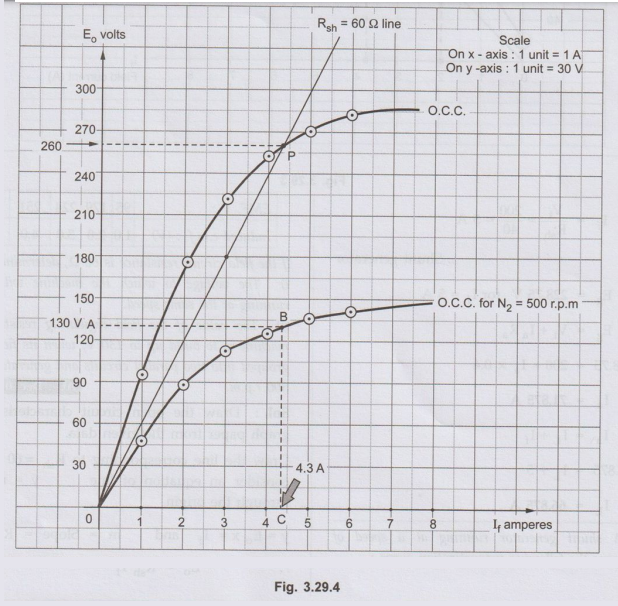
i) Thus the voltage to which the machine will build up running at the same speed is 260 V.

ii) Now generator runs at N2 = 500 r.p.m.

Draw new O.C.C. for N2 = 500 r.p.m. from above readings. Draw horizontal line of 130 V from A to meet new O.C.C. at B. Draw vertical line from B to meet lf axis at C. The corresponding current is 4.3 A.

The original 60 Ω Rsh is divided into two groups i.e. each of 30 Ω and then connected in parallel.

Field regulating resistance = 15.1162 – 15

= 0.1162 Ω

Review Questions

1. Explain the concept of critical field resistance and lacritical field.

2. The magnetization curve of a d.c. shunt generator running at 1000 r.p.m. is as follows:

Find i) The value of field resistance to give 240 V on no-load ii) The spezed at which the generator just fails to build up. [Ans.: 106.67 Ω 2, 660.38 r.p.m.]

 3. The open-circuit characteristic of a shunt o generator at 800 r.p.m. gives:

Find graphically the critical resistance of shunt field circuit. If the field circuit resistance is changed to 75 Ω, what will be the critical speed for the machine to build up? [Ans. : 586.67 r.p.m]