Curl of a Vector

Curl of a Vector

AU: Dec.-04, 06, 09, 10, 11, 12, 13, 18, May-03, 04, 10, 13, 14, 16

• The circulation of a vector field around a closed path is given by curl of a vector. Mathematically it is defined as,

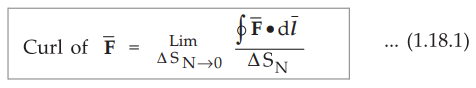
where ΔS_N = Area enclosed by the line integral in normal direction

• Thus maximum circulation of  per unit area as area tends to zero whose direction is normal to the surface is called curl of 

• Symbolically it is expressed as,

i.e.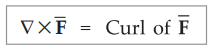 

Key Point : Curl indicates the rotational property of vector field. If curl of vector is zero, the vector field is irrotational. If 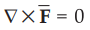 then  is irrotational.

• In various co-ordinate systems, the curl of  is given by,

Key Point : In ∂(rF_ϕ)/∂r ,r cannot be taken outside as differentation is with respect to r.

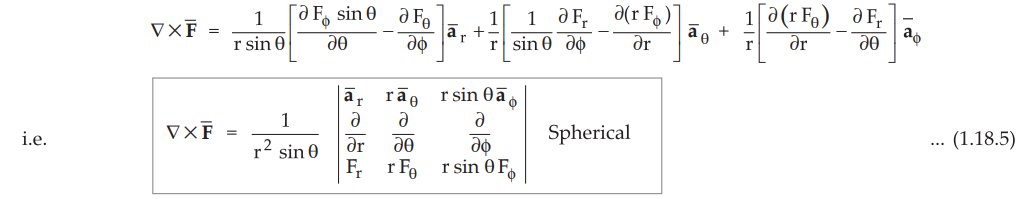
1. Physical Significance of a Curl

• The curl is a closed line integral per unit area as the area shrinks to a point. It gives the circulation per unit area i.e. circulation density of a vector about a point at which the area is going to shrink. Thus curl of a vector at a point quantifies the circulation of a vector around that point. In general if there is no rotation, there is no curl while large angular velocities means greater values of curl. The curl also gives the direction, which is along the axis through a point at which curl is defined.

• The magnetic field lines produced by the current carrying conductor are rotating in the form of concentric circles around the conductor. Thus there exists a curl of magnetic field intensity which we have defined as . The direction of curl is along the axis about which rotation of a vector field exists and the proper direction is to be obtained by right handed screw rule. If the direction of rotation of vector field about a point reverses, the sign of the curl also reverses.

• The water velocity in a river which increases linearity towards the surface, the magnetic field lines due to current carrying conductor, the body rotating about a fixed axis are few examples of a curl.

Key Point : Thus if curl of a vector field exists then the field is called rotational. For irrotational vector field, the curl vanishes i.e. curl is zero.

• Another physical interpretation of a curl is about a rigid body rotating about a fixed axis with uniform angular velocity. Thus if v is its linear velocity then its angular velocity (ω) is half the curl of its linear velocity. The curl v represents the net rotation of a body about the axis. 

2. Types of Vector Fields

• It is seen that the field  is irrotational if its curl is zero i.e. 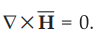. There is one more type of field called solenoidal field. The field  is said to be solenoidal if it is divergenceless i.e. 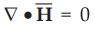 for a solenoidal field. Such a field has neither source nor a sink.

• The Table 1.18.1 gives the various type of fields.

Ex. 1.18.4 If a particular field, is given by,

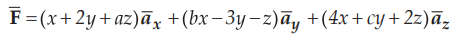
then find the constants a, b and c such that the field is irrotational.

Sol. :

Key Point : The vector field is irrotational if its curl is zero

Ex. 1.18.5 Determine the curl of the following vector fields :

 AU: Dec.-12, Marks 6

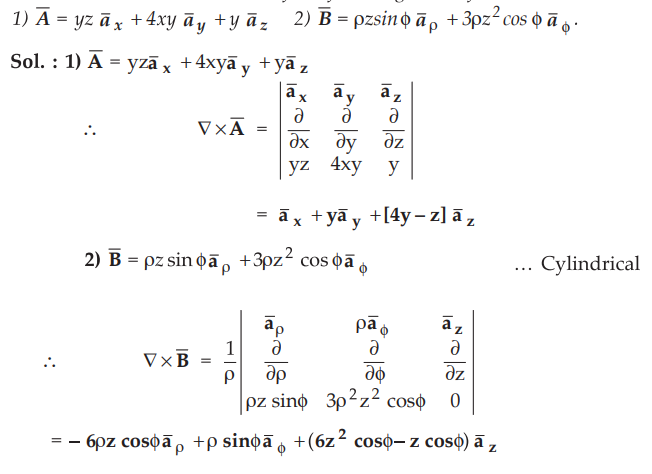
Review Questions

1. Define curl in the three co-ordinate systems with mathematical expressions. AU : May-04, 14, Dec.-04, 10,18, Marks 8

2. Describe the classification of vector fields.AU : May-13, Marks 6

3. Write a short note on curl. AU : Dec.-13, May-16, Marks 4