Cylindrical Co-ordinate System

Cylindrical Co-ordinate System 

AU : May-05, Dec.-08

• The circular cylindrical co-ordinate system is the three dimensional version of polar co-ordinate system. The surfaces used to define the cylindrical co-ordinate system are,

1. Plane of constant z which is parallel to xy plane.

2. A cylinder of radius r with z axis as the axis of the cylinder.

3. A half plane perpendicular to xy plane and at an angle with respect to xz plane. The angle ϕ is called azimuthal angle.

• The ranges of the variables are,

0 ≤ r ≤ ∞... (1.7.1)

0 ≤ ϕ ≤ 2π ... (1.7.2)

-∞ < z  ≤ ∞ ... (1.7.3)

• The point P in cylindrical co-ordinate system has three co-ordinates r, ϕ and z whose values lie in the respective ranges given by the equations (1.7.1), (1.7.2) and (1.7.3).

• The point P(r,ϕ₁,z₁) can be shown as in the Fig. 1.7.1 (b).

Key Point : Note that angle ϕ is expressed in radians and for ϕ anticlockwise measurement is treated positive while clockwise measurement is treated negative.

• The point P can be defined as the intersection of three surfaces in cylindrical co-ordinate system. These three surfaces are,

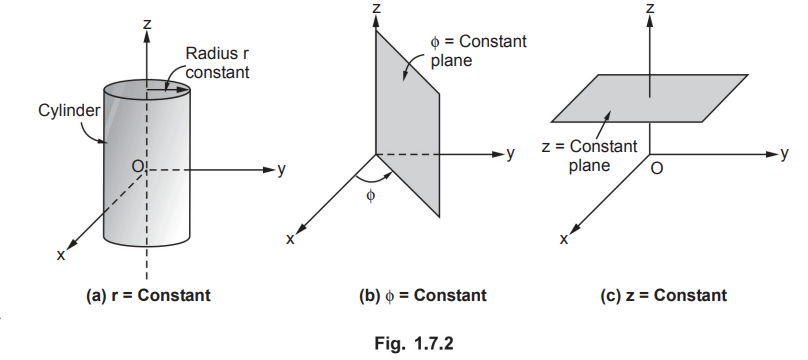
r = Constant which is a circular cylinder with z-axis as its axis.

ϕ = Constant plane which is a vertical plane perpendicular to xy plane making angle ϕ  with respect to xz plane.

z = Constant plane is a plane parallel to xy plane.

• These surfaces are shown in the Fig. 1.7.2.

• The intersection of any two surfaces out of the above three surfaces is either a line or a circle and intersection of three surfaces defines a point P.

• The intersection of z = Constant and r = Constant is a circle. The intersection of ϕ = Constant and r = Constant is a line. The point P which is intersection of all three surfaces is shown in the Fig. 1.7.3.

 

1. Base Vectors

• Similar to cartesian co-ordinate system, there are three unit vectors in the r, and z directions denoted  .

• These unit vectors are shown in the Fig. 1.7.4.

• These are mutually perpendicular to each other.

• The lies in a plane parallel to the xy plane and is perpendicular to the surface of the cylinder at a given point, coming radially outward.

• The unit vector  lies also in a plane parallel to the xy plane but it is tangent to the cylinder and pointing in a direction of increasing ϕ at the given point.

• The unit vector is parallel to z axis and directed towards increasing z.

 • Hence vector of point P can be represented as, • Thus the differential lengths are,

... (1.7.4)

where          P_r is radius r, P_ϕ is angle ϕ and P_z is z co-ordinate of point p.

Key Point : In cartesian co-ordinate system, the unit vectors are not dependent on the co-ordinates. But in cylindrical co-ordinate system  functions of co-ordinate as their directions change as changes. Hence in integration or differentiation with respect to ^components in  should not be treated constants.

 

2. Differential Elements in Cylindrical Co-ordinate System

• Consider a point P (r,ϕ,z) in a cylindrical co-ordinate system. Let each co-ordinate is increased by the differential amount. The differential increments in r, ϕ, z are dr, dϕ and dz respectively.

• Now there are two cylinders of radius r and r + dr. There are two radial planes at the angles and ϕ + dϕ. And there are two horizontal planes at the heights z and z + dz. All these surfaces enclose a small volume as shown in the Fig. 1.7.5.

• The differential lengths in r and z directions are dr and dz respectively. In ϕ direction, dϕ is the change in angle ϕ and is not the differential length. Due to this change dϕ, there exists a differential arc length in ϕ direction. differential length, due to dϕ, in ϕ direction is r dϕ as shown in the Fig. 1.7.5.

• Thus the differential lengths are,

dr = Differential length in r direction ...       (1.7.5)

r dϕ = Differential length in direction ...       (1.7.6)

dz = Differential length in z direction          ...       (1.7.7)

• Hence the differential vector length in cylindrical co-ordinate system is given by,

... (1.7.8)

• The magnitude of the differential length vector is given by,

... (1.7.9)

• Hence the differential volume of the differential element formed is given by,

 dv = r dr dϕ dz... (1.7.10)

• The differential surface areas in the three directions are shown in the Fig. 1.7.6. 

• The vector representation of these differential surface areas are given by,

3. Relationship between Cartesian and Cylindrical Systems

• Consider a point P whose cartesian co-ordinates are x, y and z while the cylindrical co-ordinates are r, and z, as shown in the Fig. 1.7.7.

• Looking at the xy plane we can write,

x = r cos ϕ and y = r sin ϕ

• The z remains same in both the systems.

Hence transformation from cylindrical to cartesian can be obtained from the equations,

x = r cos ϕ, y = r sin ϕ, and z = z... (1.7.14)

• It can be seen that, r can be expressed interms of x and y as,

r = √ x² + y²

while tan ϕ = y/x

• Thus the transformation from cartesian to cylindrical can be obtained from the equations,

r = √x² + y² , ϕ = tan^-1 y/x and z = z .....(1.7.15)

Note : While using the equations (1.7.15) note that r is positive or zero, hence positive sign of square root must be considered. While calculating ϕ make sure the signs of x and y. If both are positive, ϕ is positive in the first quadrant. If x is negative and y is positive then the point is in the second quadrant hence 6 must be within +90° and +180° i.e. within -180° and -270°. Thus for x = -2 and y = 1 we get ϕ = tan^-1[1/-2] = -26.56° but it should be taken as -26.56^o + 180° i.e. 154.43°. Hence when x is negative, it is necessary to add 180° to the ϕ calculated using tan^-1 function, to obtain accurate ϕ corresponding to the point. When y is negative and x is positive then ϕ is m fourth quadrant i.e. within 0° and -90° i.e. 270° and 360°. Similarly when x is negative and y is also negative the point is in third quadrant and accordingly ϕ must be between 0-90° to -180° i.e. +180° and +270°. So 180° must be subtracted from the 6 calculated by tan- function, to get accurate 6 when both x and y are negative. Thus if x = y = -3 then ϕ = tan^-l[-3/-3] = + 45° but actually it is 45°-180°=-135° i.e. -135°+360°=+225°.

 

Ex. 1.7.1 Find the area of the curved surface using the cylindrical co-ordinates which lies on the right circular cylinder of radius 2 m, height 8 m and 45°< ϕ <90°.

Sol. : The surface is shown in the Fig. 1.7.8.

The differential area normal to  is,

The surface is constant r surface and normal to it is unit vector .

= 2 × [90°-45°] × |π/180^o × [8 -0]

...Use ϕ in radians

2 ×45° × π ×8 / 180° = 12.5663 m²

Examples for Practice

Ex. 1.7.2 Consider a cylinder of length L and radius R. Obtain its volume by integration.[ Ans.: π R²L]

Ex. 1.7.3 Use the cylindrical co-ordinate system to find the area of the curved surface of a right circular cylinder where r = 20 m, h = 5 m and 3O°<ϕ < 120° [Ans.: 157.0796 m²]

Ex. 1.7.4 Calculate the total surface area of the cylinder having length L and radius R by the method of integration. [Ans.: 2π R(R + L)]

Review Question

1. Discuss the cylindrical co-ordinate system used to represent field vectors. AU : May-05, Dec.-08, Marks 5