D.C. Analysis of Differential Amplifier

D.C. Analysis of Differential Amplifier

May-06

The d.c. analysis means to obtain the operating point values i.e. I_CQ and V_CEQ for the transistors used. The supply voltages are d.c. while the input signals are a.c., so d.c. equivalent circuit can be obtained simply by reducing the input a.c. signals to zero. The d.c. equivalent circuit thus obtained is shown in the Fig. 2.7.1. Assuming R_S1 = R_S2, the source resistance is simply denoted by R_S.

The transistors Q₁ and Q₂ are matched transistors and hence for such a matched pair we can assume :

i) Both the transistors have the same characteristics.

ii) R_E1 = R_E2 hence RE= R_E1 || R_E2

iii) R_C1 = R_C2 hence denoted as R_C.

iv) | V_CC | = | V_EE | and both are measured with respect to ground.

As the two transistors are matched and circuit is symmetrical, it is enough to find out operating point I_CQ and V_CEQ, for any one of the two transistors. The same is applicable for the other transistor.

Applying KVL to base-emitter loop of the transistor Q₁,

From the equation (2.7.6), we can observe that

i) R_E determines the emitter current of Q₁ and Q₂ for the known value of V_EE

ii) The emitter current through Q₁ and Q₂ is independent of collector resistance R_C.

Now let us determine V_CE. As I_E is known and I_E ≅ I_C, we can determine the collector voltage of Q₁ as

V_C = V_CC - I_CR_C ...(2.7.7)

Neglecting the drop across RS we can say that the voltage at the emitter of Q₁ is approximately equal to –V_BE. Hence the collector to emitter voltage is

VCE - VC _ VE - (VCC _ ^R-C) _ ( _VBE)

VCE - VCC + VBE_ICRC      ...(2.7.8)

Hence I_E = I_C = I_CQ while V_CE = V_CEQ for given values of V_CC and V_EE.

Key Point In the equation (2.7.6), the sign of V_EE is already considered to be negative, while deriving it. Hence while using this equation to solve the problem, only the magnitude of V_EE should be used and negative sign of V_EE should not be used again.

Thus for both the transistors, we can determine operating point values, using equations (2.7.6) and (2.7.8). With the same biasing arrangement, the d.c. analysis remains same for all the four possible configurations of differential amplifier.

Key Point The d.c. analysis and expressions for I_CQ and V_CEQ remain same for all the differential amplifier circuit configurations.

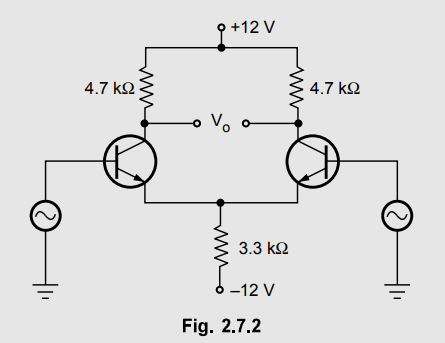
Example 2.7.1 Calculate the operating point values for the circuit shown in the Fig. 2.7.2.

Solution : From the Fig. 2.7.2 we can write

R_C = 4.7 k Ω, R_E = 3.3 k Ω, V_CC = 12V, V_EE = -12V

From equation (2.7.6),

IE = V_EE – V_BE / 2 R_E

The sign of V_EE is already considered while deriving the euqtion hence V_EE must be replaced by 12 V. And assume V_BE = 0.7 V.

Review Questions

1. Draw the circuit diagram of emitter coupled differential amplifier and obtain its d.c. analysis

2. Calculate the operating point values for the transistors shown in the Fig. 2.7.3.

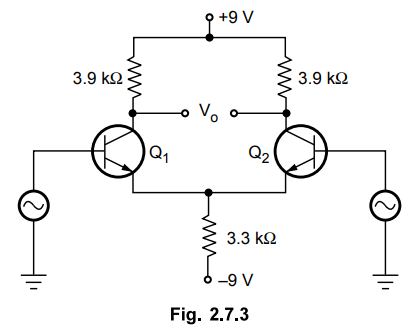
[ Ans.: 1.25 mA, 4.825 V ]

3. For a differential amplifier circuit operated from  ± 5 V, assume V_BE = 0.7 V and h_fe = 100. If R_c for each is 100 k Ω, calculate the value of R_E so that the quiescent collector emitter voltage for each transistor is 4 V.    

[ Ans.: 125 k Ω ]