DAC (Digital to Analog Converter) using Op-amp

D/A Converters

May-03, 04, 05, 06, 07, 08, 09, 10, 11, 12, 15, 17,

Dec.-03, 04, 05, 06, 07, 08, 09, 10, 11, 12, 17

A DAC (Digital to Analog Converter) accepts an n-bit input word b₁, b₂, b₃, ... b_n in binary and produce an analog signal proportional to it. Fig. 3.25.1 shows circuit symbol and input-output characteristics of a 4-bit DAC. There are four digital inputs, indicating 4-bit DAC. Each digital input requires an electrical signal representing either a logic 1 or a logic 0. The bn is the least significant bit, LSB, whereas b 1 is the most significant bit, MSB.

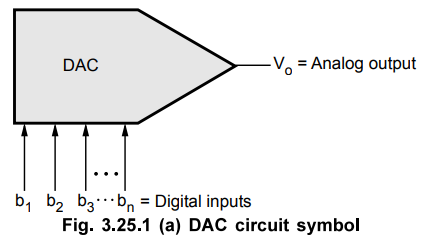
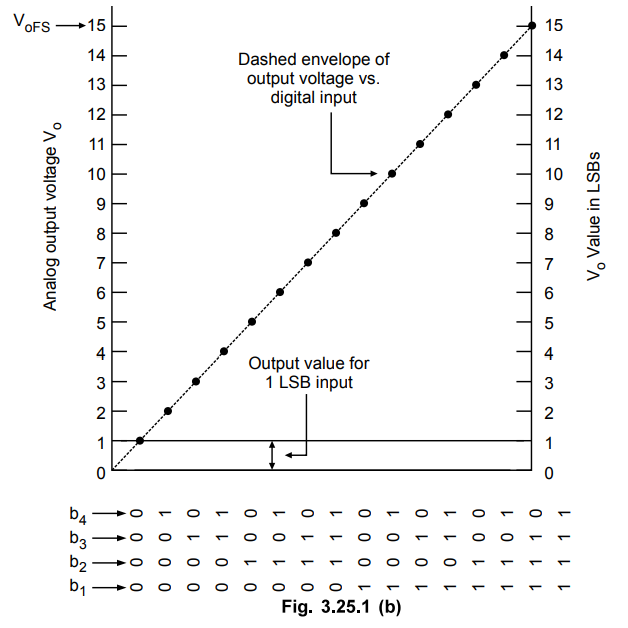
Fig. 3.25.1 (b) shows analog output voltage Vo is plotted against all 16 possible digital input words.

1. Performance Parameters of DAC

The various performance parameters of DAC are,

a. Resolution

Resolution is defined in two ways.

• Resolution is the number of different analog output values that can be provided by a DAC. For an n-bit DAC

Resolution = 2ⁿ    ... (3.25.1)

• Resolution is also defined as the ratio of a change in output voltage resulting from a change of 1 LSB at the digital inputs. For an n-bit DAC it can be given as

Resolution = V_oFS / 2ⁿ – 1 ... (3.25.2)

where,         V_oFS  = Full scale output voltage 

From equation (3.25.1), we can say that, the resolution can be determined by the number of bits in the input binary word. For an 8-bit DAC resolution can be given as

Resolution = 2ⁿ = 2⁸

= 256

If the full scale output voltage is 10.2 V then by second definition the resolution for an 8-bit DAC can be given as

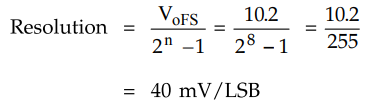
Therefore, we can say that an input change of 1 LSB causes the output to change by 40 mV.

From the resolution, we can obtain the input-output equation for a DAC.

Thus  V_o =  Resolution × D

where  D =   Decimal value of the digital     input

and    V_o =  Output voltage

The resolution takes care of changes in the input.

b. Accuracy

It is a comparison of actual output voltage with expected output. It is expressed in percentage. Ideally, the accuracy of DAC should be, at worst, ±  1/2 its LSB. If the full scale output voltage is 10.2 V then for an 8-bit DAC accuracy can be given as

Accuracy = V_oFS / (2n – 1)2   …. (3.25.3)

= 10.2 / 255 × 2 = 20mV

c. Monotonicity

A converter is said to have good monotonicity if it does not miss any step backward when stepped through its entire range by a counter.

d. Conversion Time

It is a time required for conversion of analog signal into its digital equivalent. It is also called setting time. It depends on the response time of the switches and the output of the amplifier. 

e. Settling Time

This is the time required for the output of the DAC to settle to within ±1/2 LSB of the final value for a given digital input i.e. zero to full scale.

f. Stability

The performance of converter changes with temperature, age and power supply variations. So all the relevant parameters such as offset, gain, linearity error and monotonicity must be specified over the full temperature and power supply ranges. These parameters represent the stability of the converter.

Example 3.25.1 An 8-bit DAC has an output voltage range of 0-2.55 V. Define its resolution in two ways.

Solution : For the given DAC,

n = Number of bits = 8

i) Resolution = 2ⁿ = 2⁸ = 256

i.e. the output voltage can have 256 different values including zero.

ii) V_oFS = Full scale output voltage

= 2.55 V

Resolution = V_oFS / 2_n -1 = 2.55 / 2⁸ - 1

10mV / 1 LSB

Thus an input change of 1 LSB causes the output to change by 10 mV.

Example 3.25.2 The digital input for a 4-bit DAC is 0110. Calculate its final output voltage.

Solution : For given DAC,

n = 4

V_oFS = 15 V

Resolution = V_oFS / 2ⁿ -1 = 15 / 2⁴ – 1 = 1V/LSB

V_o = Resolution × D

Now D = Decimal of (0110)₂ = 6

V_o = 1 V/LSB × 6 = 6 V

Example 3.25.3 An 8-bit DAC has resolution of 20 mV/LSB. Find V_oFS and V_o if the input is (10000000)₂.

Solution :

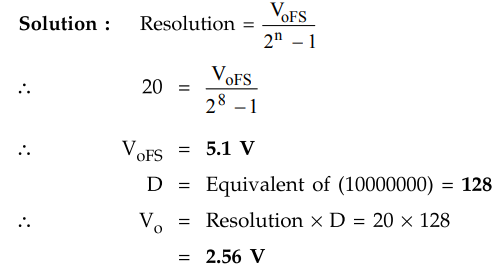
Example 3.25.4 Find out stepsize and analog output for 4-bit R-2R ladder DAC when input is 1000 and 1111. Assume V_ref = +5 V.

Solution : For given DAC, n = 4, V_oFS = +5 V

Resolution = V_oFS / 2ⁿ-1 = 5 / 2⁴-1 = 1/ 3 V / LSB

V_o = Resolution × D

For = Decimal of (1000)₂ = 8

V_o = 1/ 3 × 8 = 2.6667 V

For  D = Decimal of (1111)₂ =15

V_o = 1 / 3 ×15 = 5V.

Example 3.25.5 A 12-bit DAC has a step size of 8 mV. Determine the full scale output voltage and percentage resolution. Also find the output voltage for the input of 010101101101?

Solution : For 12-bit DAC, step size is 8 mV.

V_oFS = 8mV × 2¹² -1 = 32.76 V 8mV

% Resolution = 8mV / 32.76V × 100 = 0.02442 %

The output voltage for the input 010101101101 is = 8 mV × (1389)₁₀ = 11.112 V

Example 3.25.6 Determine the output voltage produced by a 4-bit DAC whose output voltage range is 0 to 10 V when the input binary number is 0110.

Dec.-03, Marks 6

Solution : Given  V_oFS = 10 V

Resolution = 10 / 2⁴ – 1 = 0.6667 V

The output voltage at 0110 = 0.6667 × 6 = 4 V

Example 3.25.7 Suggest the values of resistors and reference voltage if resolution required is 0.5 V for 4-bit R/2R ladder type DAC.

Solution :

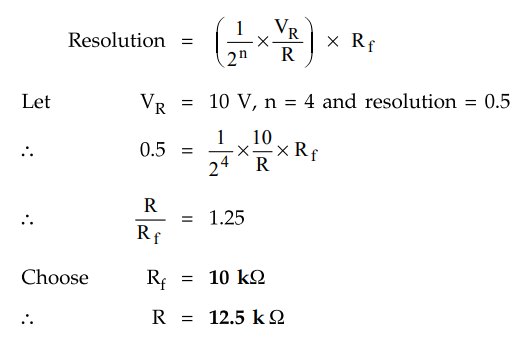
2. Types of D/A Converter

There are mainly two techniques used for analog to digital conversion

• Binary weighted resistor D/A converter

• R/2R ladder D/A converter

In these techniques, the shunt resistors are used to generate n binary weighted currents. These currents are added according to switch positions controlled by the digital input and then converted into voltage to give analog voltage equivalent to the digital input. Therefore, such digital to analog converters are called current driven DACs.

a. Binary Weighted Resistor D/A Converter

The binary weighted resistor DAC uses an op-amp to sum n binary weighted currents derived from a reference voltage VR via current scaling resistors 2R, 4R, 8R, ..., 2ⁿ R, as shown in the Fig. 3.25.2

As shown in the Fig. 3.25.2, switch positions are controlled by the digital inputs. When digital input is logic 1, it connects the corresponding resistance to the reference voltage VR; otherwise it leaves resistor open. Therefore,

For ON-switch, I = V_R / R and 

For OFF-switch, I = 0

Here, operational amplifier is used as a summing amplifier. Due to high input impedance of op-amp, summing current will flow through Rf. Hence the total current through Rf can be given as

I_T = I₀ +I₁ + I₂ + … + I_n

The output voltage is the voltage across Rf and it is given as

The equation (3.25.4) indicates that the analog output voltage is proportional to the input digital word.

The simplicity of the binary weighted DAC is offset by drawbacks associated with it.

Drawbacks :

1. Wide range of resistor values are required. For 8-bit DAC, the resistors required are 2¹ R, 2² R, 2³ R,... and 28 R. Therefore, the largest resistor is 128 times the smallest one. 

2. This wide range of resistor values has restrictions on both, higher and lower ends. It is impracticable to fabricate large values of resistor in IC, and voltage drop across such a large resistor due to the bias current also affects the accuracy. For smaller values of resistors, the loading effect may occur.

3. The finite resistance of the switches disturbs the binary-weighted relationship among the various currents, particularly in the most significant bit positions, where the current setting resistances are smaller.

All these drawbacks, especially the requirement of wide range of resistors restricts the use of binary weighted resistor DACs below 8-bits.

b. Inverted R-2R Ladder I Current Mode R-2R Ladder D/A Converter

R/2R ladder D/A converter uses only two resistor values. This avoids resistance spread drawback of binary weighted D/A converter. Fig. 3.25.3 shows R/2R ladder DAC. Like binary weighted resistor DAC, it also uses shunt resistors to generate n binary weighted currents; however it uses voltage scaling and identical resistors instead of resistor scaling and common voltage reference used in binary weighted resistor DAC. Voltage scaling requires an additional set of voltage dropping series resistances between adjacent nodes, as shown in the Fig. 3.25.3.

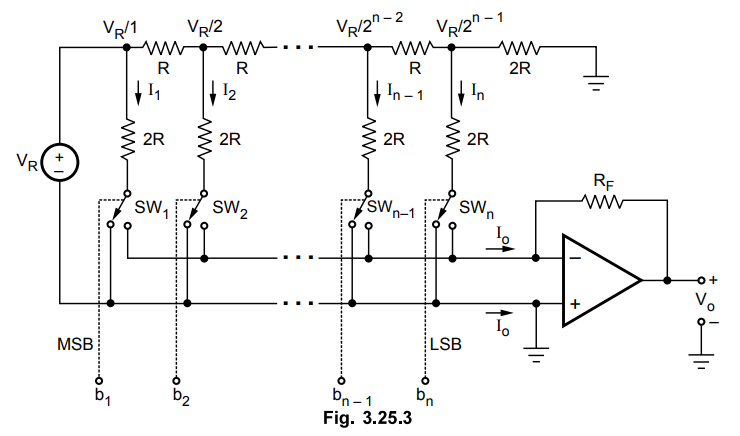
Here, each bit of the binary word connects the corresponding switch either to ground or to the inverting input terminal of the op-amp which is at the virtual ground. Since both the positions of switches are at ground potential, the current flowing through resistances is constant and it is independent of switch position. These currents can be given as,

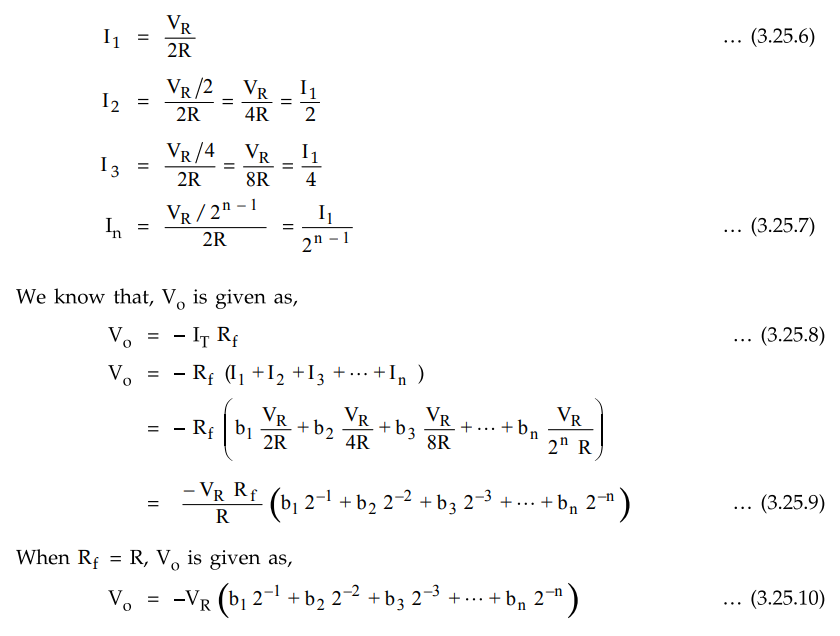
Let us consider 4-bit binary DAC with binary input 1001 and Rf = R, as shown in the Fig. 3.25.4.

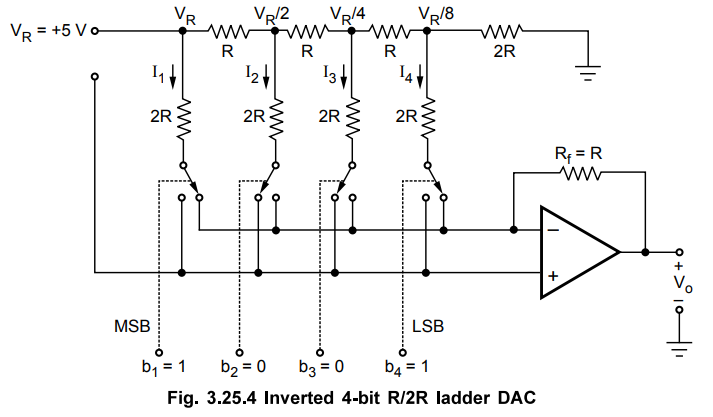
Here, output voltage is given as

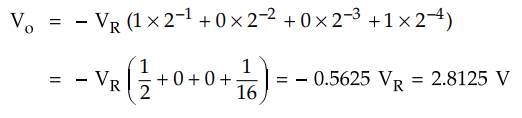
The inverting R/2R ladder DAC works on the principle of summing currents and it is also said to operate in the current steering mode. An important advantage of the current mode is that all ladder node voltages remain constant with changing input codes, thus avoiding any shutdown effects by stray capacitances.

c. R-2R Ladder I Voltage Mode R-2R Ladder D/A Converter

In this type, reference voltage is applied to one of the switch positions, and other switch position is connected to ground, as shown in the Fig. 3.25.5.

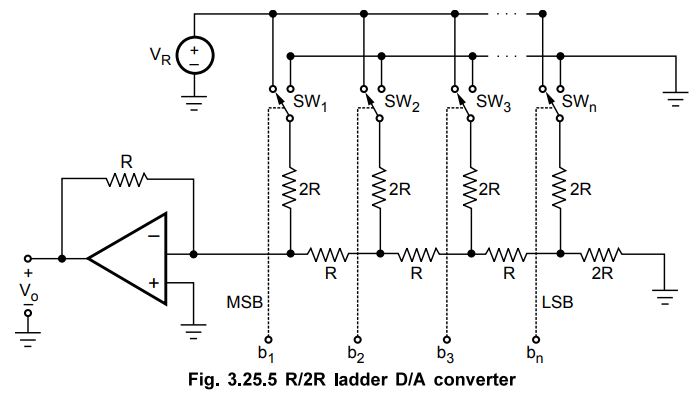
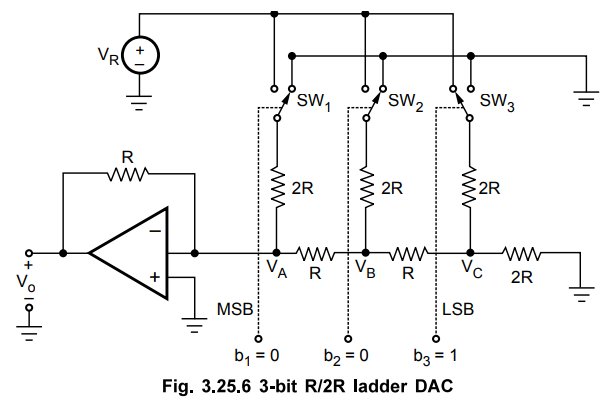
Let us consider 3-bit R/2R ladder DAC with binary input 001, as shown in the Fig. 3.25.6.

Reducing above network to the left by Thevenin's theorem we get,

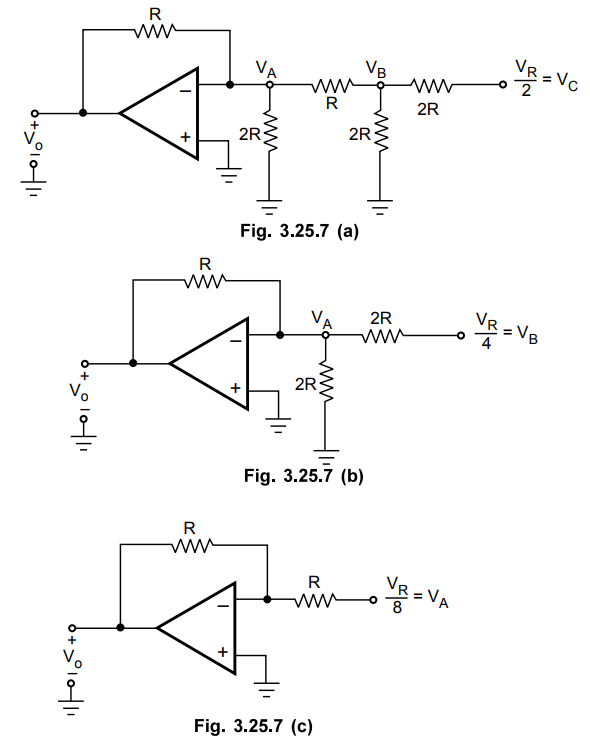
Therefore, the output voltage is VR/8 which is equivalent to binary input 001. For binary input 100 the network can be reduced as follows :

Therefore, the output voltage is V_R/2, which is equivalent to binary input 100. In general, the voltage is given by

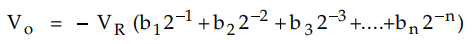
The expression for V_o can be obtained as,

Let I_out - Output current

R_f = Feedback resistance of op-amp

V_o =  - I_out R_f

Now I_out = Current resolution × D

V_o = (Current resolution × D) R_f

V_o = (Current resolution × R_f) × D  ….. (3.25.11)

The coefficient of D is the voltage resolution and can be called simple resolution.

V_o = - Resolution ×D (Binary data)  ... (3.25.12)

In terms of actual circuit elements, output can be written as,

V_o =  - (V_R / R × 1 / 2ⁿ R_f ….. (3.25.13)

The resolution of R/2R ladder type DAC with current output is,

Resolution = 1 / 2ⁿ × V_R / R  … (3.25.15)

while the resolution for R/2R ladder type DAC with voltage output is,

Resolution = (1 / 2ⁿ × V_R / R) × R_f … (3.15.15)

3. Sources of Errors in DAC

There are mainly three errors in DACs : Linearity, Offset and gain errors.

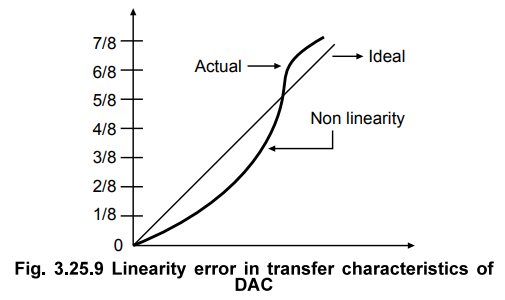
a. Linearity Error

The error is defined as the amount by which the actual output differs from the ideal straight-line output.

Fig. 3.25.9 shows the linearity error in the transfer characteristics of DAC. It is mainly due to the errors in the current source resistor values

b. Offset Error

The offset error is defined as the nonzero level of the output voltage when all inputs are zero.

It adds a constant value to all output values, as shown in Fig. 3.25.10.

It is due to the presence of offset voltage in op-amp and leakage currents in the current switches.

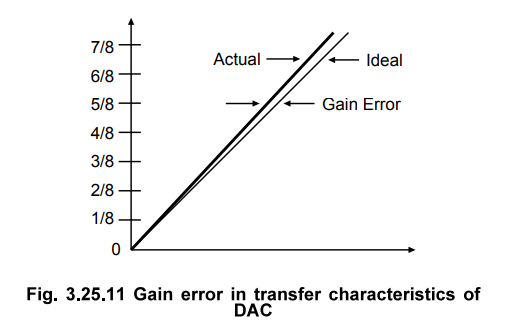
c. Gain Error  

The gain error is defined as the difference between the calculated gain of the current to voltage converter and the actual gain achieved. It is due to the errors in the feedback resistor on the current to voltage converter op-amp.

Fig. 3.25.11 shows the gain error in transfer characteristics of DAC.

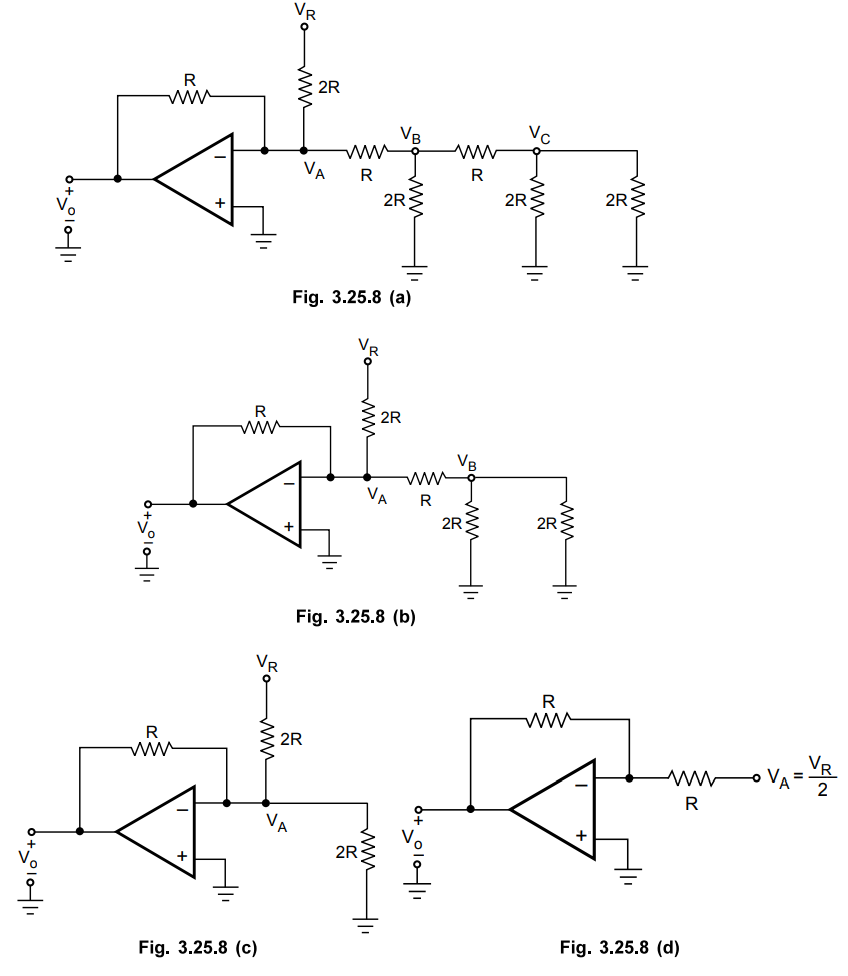
Example 3.25.8 Design a 4 bit R-2R ladder network, determine the size of each step if R = 10 kΩ, R_f = 20 kΩ and V_CC = ± 15 V. Calculate the output voltage for D_o = 1, D₁ = 0, D₂ = 1 and D₃ = 1 if bit '1' applied as 5 V and bit 'O' applied as 0 V.

May-13, Marks 8

Solution : Fig. 3.25.12 shows 4-bit R-2R ladder. 

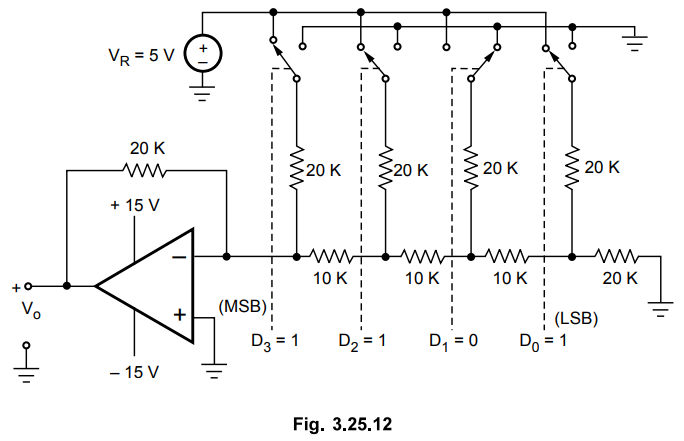
The output voltage for DAC shown in Fig. 3.25.12 is given by

Review Questions

1. Explain the weighted resistor DAC with neat sketch.

May-06, Dec.-11, 17, Marks 8

2. Explain in detail about R-2R ladder DAC and inverted R-2R ladder DAC alongwith relevant circuit diagrams and waveforms.

Dec.-03, 07,09, May-04, 06, 11, Marks 16

3. Explain the important DAC specifications.

May-12, Dec.-12, Marks 4

4. With neat circuit diagram explain the operation of R-2R D/A converter

May-15, 17, Dec.-17, Marks 8