DC transients

DC TRANSIENTS

Here we have three types of circuits. In each case the voltage applied (excitation) is assumed to be step voltage denoted by Eu (t). u (t) is the unit step voltage.

1. (a) Case 1: (a) R-L Transients: (Rise of Current)

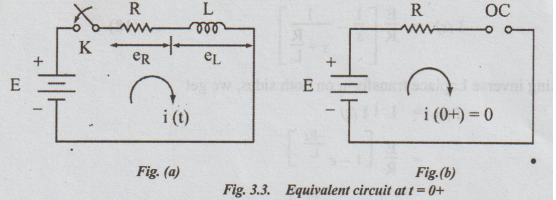
Let the R – L  series combination be impressed upon the d.c. voltage E by closing the switch K. Assume that the current through the inductor before closing the switch is zero. Let K be closed at the instant t = 0.

The equivalent circuit at t=0+ is shown in fig. 3.3 (b). The inductor is shown as open circuit. Hence i (0-) = i(0+) = 0.

Applying KVL to the circuit in fig. 3.3 (a), after t seconds of closing K,

we get, Ri + L di / dt = E … (15)

Taking Laplace Transformation on both sides, we get

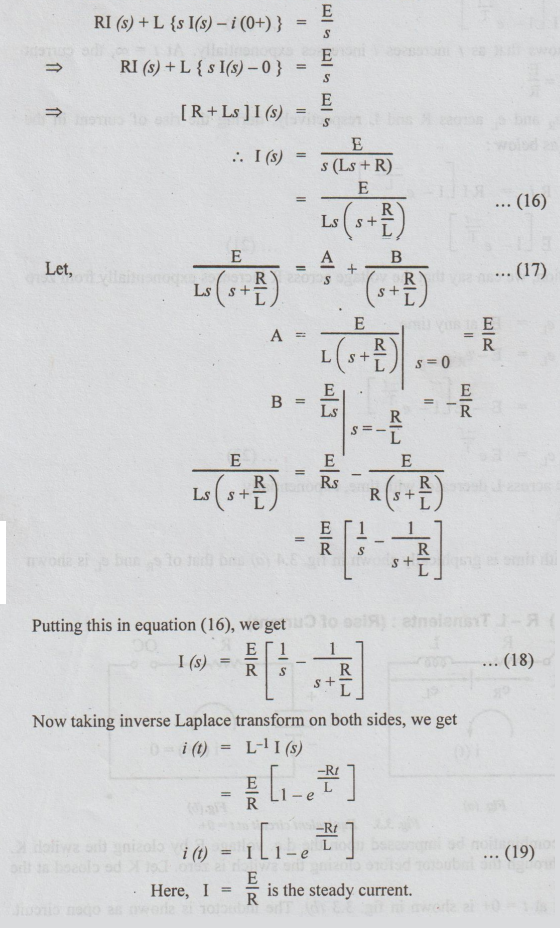
Steady current is thevalue of I (t) for t = ∞

L/R is called time constant of the RL circuit and is denoted by T.

Hence equation (19) can be written as

I = I [I – e ^–t/T] … (20)

The above equation shows that as t increases i increases exponentially. At t = ∞, the current reaches steady state value I = E / R.

The transient voltage e_R and e_L across R and L respectively, during the rise of current in the inductive can be expressed as below:

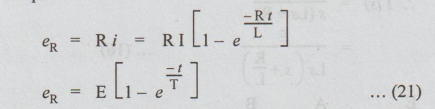
From the above expression, we can say that the voltage across R increases exponentially from zero to E, during rise of current.

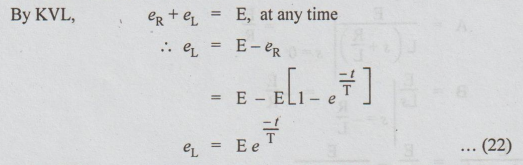
It shows that the voltage across L decreases with time, exponentially

[Note: e_L = - L di / dt]

The variation of i (t) with time is graphically shown in fig. 3.4 (a) and that of in fig. 3.4 (b).

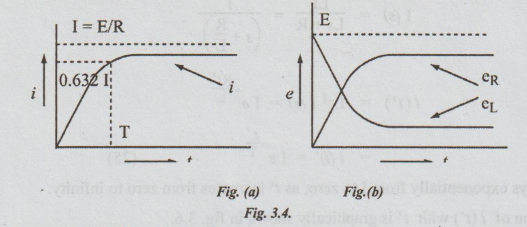
Definition of time constant T for RL circuit

Substituting T = t in equation (20), we get

i = I (1 – e^-1)

= 0.632 I

= 63.2% of I

Thus the time constant of RL series circuit is defined as the period during which the current rises to 63.2% of its final value (OR steady value).

(b) RL-Decaying Transients

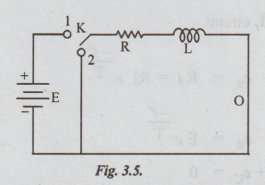
Assume that the switch K is kept connected to position 1 for sufficiently longer period. Then the current reaches steady state value given by I = E  / R. After this instant, let the switch be moved from position 1 to position 2. Let this instant be taken as t = 0. After t' seconds of closing the switch to position, applying KVL,

Ri+ L di / dt’ = 0  … (23)

Taking Laplace Transformation on both sides, we get

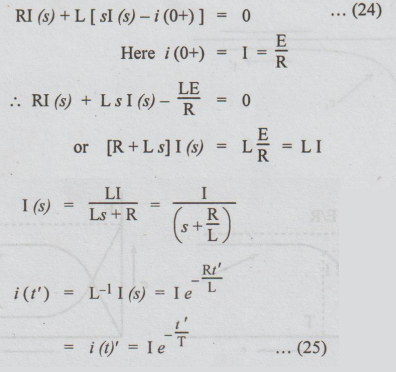
Thus i decays exponentially from I to zero, as t' increases from zero to infinity. The variation of i (t') with t' is graphically shown in fig. 3.6.

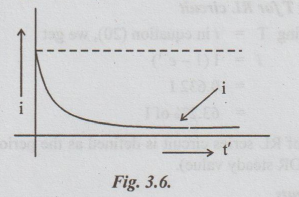
Decaying current in an R - L circuit.

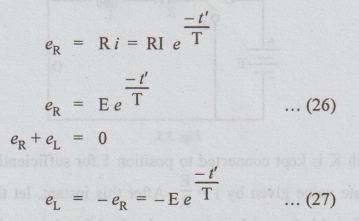
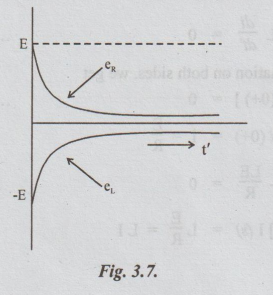
The variation of er and e, with t' is graphically shown in fig. 3.7.