Two Marks Questions with Answers

UNIT – II

DESIGN OF EXPERIMENTS

'2' MARKS QUESTIONS AND ANSWERS

 

1. Define "Analysis of Variance." (or) ANOVA.

According to R.A. Fisher, Analysis of variance (ANOVA) is the 'separation of variance ascribable to one group of causes from the variance ascribable to other groups'.

2. The basic purpose of the analysis of variance is to test the homogeneity of .......

[A.U A/M 2019 R-17]

[Ans. several means.]

 

3. Define "experimental error". [A.U N/D 2016 R-13]

The estimation of the amount of variation due to each of the independent factors separately and then, comparing these estimates due to assignable factors with the estimate due to the chance factor is known as experimental error or simple error.

 

4. Write down the Assumptions in Analysis of variance.

1. Normality, 2. Homogeneity, 3. Independence of error.

 

5. Explain the word 'treatment' in analysis of variance.

The word treatment in analysis of variance is used to refer to any factor in the experiment that is controlled at different levels or values.

 

6. What are the uses of analysis of variance? [A.U A/M 2017 R13]

1. To test the homogeneity of several means.

2. The ANOVA technique is now frequently applied in testing the linearit of the fitted regression line or the significance of the correlation ratio ƞ.

 

7. What do you mean by one-way classification in analysis of variance?

In one-way classification the datas are classified according to only one AVOMA criterion (or) factor.

 

8. What do you mean by two-way classification in analysis of variance?

In a two-way classification the datas are classified according to two different criteria or factors.

 

9. Define Mean sum of squares.  [A.U N/D 2011]

Mean Sum of Squares (M.S.S). The sum of square divided by its degrees of freedom gives the corresponding variance or the mean sum of squares (M.S.S.). Thus,

 

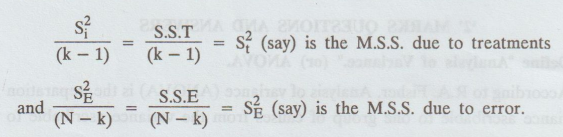
10. Explain the term "Normality".

The values in each group are normally distributed.

 

11. Explain the term "Homogeneity".

The variance within each group should be equal for all groups (σ²₁ = σ²₂ .... = σ²_c ). This assumption is needed in order to combine or pool the variances within the groups into a single within groups' source of variation.

 

12. Explain the term Independence of error.

It states that the error (variation of each value around its own group mean) should be independent for each value.

 

13. Discuss the advantages of the two-way classification method over one-way classification, if any. no ni noted brow [A.U N/D 2011]

1. In two-way classification method, we can test two sets of hypothesis with the same data at the same time but in one-way classification method, we cannot test two sets of hypothesis.

2. In a one-way classification method of analysis of variance, the treatments constitute different levels of a single factor which is controlled in the experiment. There are however, many situations in which the response variable of interest may be affected by more than one factor. That is solved by two way classification method of a time.

 

14. What is ANOVA ? [A.U N/D 2016 R-13]

The technique of analysis of variance is referred to as ANOVA. A table showing the source of variation, the sum of squares, the degrees of freedom, mean squares (variance) and the formula for F-ratio is known as ANOVA table.

 

15. Explain the meaning and use of analysis of variance.

Analysis of variance to test the homogeneity several means.

Uses

1. It helps to find out the F-test.

2. Between the samples, we can find the variances.

 

16. What are the assumptions involved in ANOVA ?

Solution:   [A.U A/M 2010] [A.U N/D 2019 R-17]

1. The samples are drawn from normal populations.

2. The variances for the population from which samples have been drawn are equal.oads on

om103

3. The variation of each value around its own grant mean should be anom independent for each value.

 

17. Write the basic steps in ANOVA.  [A.U Trichy N/D 2010]

Solution :

1. One estimate of the population variance from the variance among the sample means.

2. Determine a second estimate of the population variance from the variance within the sample.

3. Compare these two estimates, if they are approximately equal in value, a) accept the null hypothesis.

 

18. What are the Basic principles in the design of experiment ? do ad [A.U A/M 2015 R-13, M/J 2016 R-13] [A.U A/M 2017 R-13] [A.U A/M 2019 (R-17), N/D 2019 (R-13), N/D 2021 (R-17)]

There are three basic principles of experimental design.

They are: (1) Randomization, (2) Replication, (3) Local control (error control)

 

19. Construct 4 × 4 Latin square design. [A.U CBT M/J 2010]

Solution:

Each symbol appears one and only once in each row and column.

 

20. What do you understand by "Design of an experiment" ? nisiq [A.U. M/J 2013] [A.U A/M 2015 R-13] [A.U N/D 2017 R-13]

The design of an experiment may be defined as "the logical construction of the experiment in which the degree of uncertainty with which the inference is drawn may be well defined.

 

21. Explain the purpose of design of experiments, and indicate the characteristics of a good experimental design.

An experiment is a device or a means of getting an answer to the problem under consideration. Experiment can be classified into two categories as follows: (a) Absolute and (b) Comparative.

Absolute experiments consists in determining the absolute value of some characteristic like (i) obtaining the average intelligence quotient (I.Q) of a group of people, (ii) finding the correlation coefficient between two variables in a bivariate distribution etc. On the other hand comparative experiments are designed to compare the effect of two or more objects on some population characteristic, (e.g.,) comparison of different manures or fertilizers, different kinds of varieties of a crop, different cultivation processes, different pieces of land in a field experiment, or different diets or medicines in a dietary or medical experiment respectively, etc.

 

22. Define Experimental Error, what are its main sources? What methods are adopted to increase the accuracy of an experiment?

Experimental Error. Suppose, a large homogeneous field is divided into different plots (of equal shape and size) and different treatments are applied to these plots if the yields from some of the treatments are more than those of the others, the experimentor is faced with the problem of deciding whether the observed differences are really due to treatment effects or they are due to chance (uncontrolled) factors. In field experimentation, it is a common experience that the fertility gradient of the soil does not follow any systematic pattern but behaves in an erratic fashion. Experience tells us that even if the same treatment is used on all the plots, the yields would still vary due to the differences in soil fertility. Such variation from plot to plot, which is due to random (or chance or non-assignable) factors beyond human control, is spoken an experimental error.

Main Sources are :

(i) the inherent variability in the experimental material to which treatments are applied,

(ii) the lack of uniformity in the methodology of conducting the experiment or in other words, failure to standardize the experimental technique, and

(iii) lack of representativeness of the sample to the population under study.

The following methods are adopted to increase the accuracy of an experiment. 1. replication, 2. local control.

 

23. What are the advantages of the Latin square design over other designs. [A.U Tvli M/J 2011] [A.U A/M 2015 R-8]

The advantages of the Latin Square design over other designs are:

(i) With a two-way stratification or grouping, the Latin Square controls more of the variation than the completely randomized design or the randomized block design. The two-way elimination of variation often results in small

(ii) The analysis is simple, it is only slightly more complicated than that for  the randomized complete block design.

(iii) The analysis remains relatively simple even with missing data. Analytical procedures are available for omitting one or more treatments, rows, or columns.

However, the number of treatments is limited to the number of rows and columns - except in some situations. For more than ten treatments, the Latin square is seldom used.

 

24. What are the advantages of a completely Randomized Experimental design? [A.U N/D 2011] [A.U A/M 2019 R-13]

The following are the main advantages of this type of design :

1. It is easy to layout the design.

2. It allows for complete flexibility. Any number of factor classes and replications may be used.

3. The statistical analysis is relatively simple, even if we do not have the same number of replicates for each factor class or if the experimental errors are not the same from class to class of this factor.

4. The method of analysis remains simple, when data are missing or rejected and the loss of information due to missing data is smaller than any other design.

 

25. Completely Randomized Design (CRD) : [A.U N/D 2017 R-13] [A.U N/D 2017 R-8]

Merits:

(i) It has a simple layout.

(ii) The analysis of the design is simple as it results in a one-way classification analysis of variance.

(iii) There is complete flexibility as the number of replication is not fixed.

(iv) Analysis can be performed, if some observation are missing.

Demerits

The experimental error is large as compared to the other designs because homogeneity of the units is not taken into consideration.

 

26. Why a 2 × 2 Latin square is not-possible? Explain.

[AU 2006] [A.U A/M 2015 R-8, N/D 2015 R-13, M/J 2016 R-13] [A.U N/D 2019 R-13]

Consider, a n × n Latin square design, then the degrees of freedom for SSE is

= (n²  -1) - (n - 1) (n - 1) (n - 1)

= n² - 1 - 3n + 3

= n² - 3n + 2

= (n-1) (n-2)

For n = 2, d.f of SSE = 0 and hence, MSE is not defined.

comparisons are not possible. Hence, a 2 × 2 Latin Square Design is not possible.

 

27. Compare and contrast LSD and RBD. [AU 2003, A.U CBT N/D 2011, A.U. M/J 2013]

 

28. What is the main aim of design of experiments? [A.U N/D 2019 R-17]

Solution :

The main aim of design of experiment is to control the extraneous variables and to minimize the error so that the results of experiments could be attributed to the experimental variables only.

 

29. Define a treatment and a yield in an experimental design. [A.U N/D 2020, A/M 2021]

Treatment: The word treatment in analysis of variance is used to refer to any factor in the experiment that is controlled at different levels or values.

Yield: The measurement of a specific variable on different experimental units for example different patients in a hospital in a medical experiment is called yield.

 

30. What is contrast and orthogonal contrast in a 22-factorial design? [A.U N/D 2020, A/M 2021 (R-17)]

Solution :

Contrast is a linear combination of treatment means, such that the sum of the co-efficients is zero.

The contrasts are orthogonal if the sum of product of co-efficients of corresponding treatment means is zero.

 

31. State the basic designs of experiment. [A.U N/D 2021 (R-17)]

Solution :

1. Completely Randomised Design (CRD)

2. Randomized Block Design [RBD]

3. Latin Square Desgin [LSD]