Electric Circuit Analysis: Unit III: Transient Response Analysis
Determination of initial conditions
Transient Response Analysis
The procedure generally followed to determine the initial conditions consists of two steps in sequence.
DETERMINATION OF INITIAL CONDITIONS
The
procedure generally followed to determine the initial conditions consists of
two steps in sequence.
Step
1: Solving for initial values of variables at t =
(0+).
For
this, the following rules are to be followed:
(i)
Replace every inductor by an open circuit or by a current generator having
source current equal to that flowing at t = (0+).
(ii)
Replace every capacitor by short circuit or by a voltage generator having
source voltage
Vco
= q0 / C
(iii) Leave every resistor in the network
unchanged.
Step
2: Solving for the initial values of derivatives at t
= 0+.
The
details and the order of mathematical manipulation involved for the derivatives
will be different for each different case.
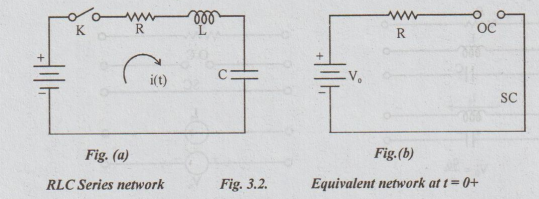
Consider
a series RLC network shown in fig. 3.2(a). It is connected to a DC voltage
source V0 at t = 0. Assume that no voltage has been applied to the
network before t = 0.
It
is required to find it i (0+), di / dt (0+) and d'i / dt2 (0+).
F
Step
1: The equivalent network of fig.3.2 (a) is as shown
in fig. (b), at t=0+. Here inductor is shown by an open circuit and capacitor
is shown by short circuit. It is by assuming that initial current through
inductor and voltage across capacitor are equal to zero.
From
fig. (b). We see that i (0+) = 0. Applying Kirchoff's voltage law to the given
network we get,
L
di / dt + Ri + 1/C ∫ idt = V0 ... (11)
Equation
(11) holds at t = 0+. Also at t = 0+, i = 0 and 1/C ∫ idt = 0. This last term
is the voltage across the capacitor at t = 0+. Putting these values in equation
(11) at t = 0+, we get L di / dt (0+) = V0
di
/ dt (0+) dt = V0/L ... (12)
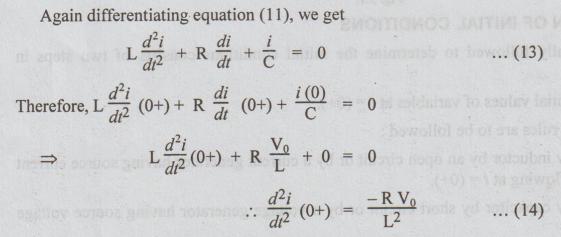
Electric Circuit Analysis: Unit III: Transient Response Analysis : Tag: : Transient Response Analysis - Determination of initial conditions
Electric Circuit Analysis: Unit III: Transient Response Analysis
Under Subject
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation