Difference between series and parallel circuits

DIFFERENCE BETWEEN SERIES AND PARALLEL CIRCUITS

 

EXAMPLE 9: Figure shows 3 resistors RA, RB and Rc connected in series to a 250 V source. Given R_e = 50 Q, and V_B = 80 Volts when the current is 2 amperes, calculate the resistances R_A and R_B.

Solution

Current flowing through the circuit, I = 2 A

Voltage across resistor R_B, V_B = 80 V

V_B = IR_B

R_A = 35 Ω

 

EXAMPLE 10: A resistor of ohmic value 30 22 is connected in series with an unknown resistor. The potential drop across the two resistors are 144 V and 96 V respectively. Find the value of the unknown resistor.

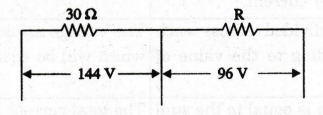
Solution

Let the current flowing through the two resistors be I

Then, voltage across the 30 Ω resistor = 30 I = 144 V

Therefore, I = 144 / 30 =  4.8 A

Let the unknown resistor be R ohms. The voltage drop across R is

IR = 96 V

Therefore, R = 96 / I =  96 / 4.8 = 20 Ω

R = 20 Ω

 

EXAMPLE 11: Two resistors connected in parallel across 200 V supply take 10 A from the mains. If the power dissipated in one resistor is 800 W, find the value of the other resistor.

Solution

Total power taken P = V × I = 200 × 10 = 2000 W

Power dissipated in one resistor P₁ = 800 W

Therefore, power dissipated in the other resistor

R = 32.33 Ω

 

EXAMPLE 12: A lamp rated 500 W, 100 V is to be operated from 220 V supply. Find the value of the resistor to be connected in the series with the lamp. How much power is lost in the resistor?

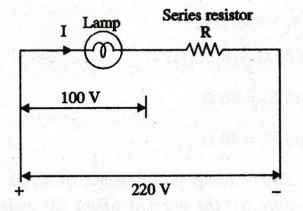
Solution

Current in the lamp = P/V = 500 / 100 = 5 A

Since voltage drop across the lamp is 100 V, voltage to be dropped in the series resistor 220-100 120 V.

Therefore, value of the resistor R = 120 / 5 = 24Ω

Power lost in the resistor I² × R = 5² × 24 = 600 W.

 

EXAMPLE 13: The effective resistance of two resistors connected in series is 100 9. When connected in parallel, the effective value is 24 2. Determine the values of the two resistors.

Solution

Let the two resistors be R₁ and R₂

When in series, R₁ + R₂ = 100 Ω

R₂ = 100 – R₁

 

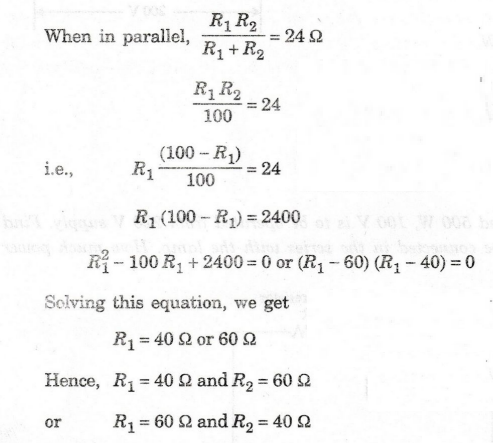
EXAMPLE 14: A 60 W, 240 V lamp is connected in series with a 40 W, 200 V lamp across 250V supply. Calculate (i) the current taken (ii) voltage across each lamp and (iii) power given by the lamps. Assume that the resistance of the lamps remains constant.

Solution

Resistance of 60 W lamp = V² / P = (240)² / 60 = 960 Ω

Resistance of 40 W lamp = V² / P = (200)² / 40 = 1000 Ω

When both lamps are in series, total resistance is the sum of the resistances of each lamp.

i.e; R_total = 960 + 1000 = 1960 Ω

(i) Current = V / R_total  = 250 / 1960 = 0.12755 A

(ii) Voltage across 60 W lamp = 0.12755 × 960 = 122.45 V

Voltage across 40 W lamp = 0.12755 × 1000 = 127.55 V

(iii) Power (Lamp 1) = 0.12755 × 122.45 = 15.62 W

Power (Lamp 2) = 0.12755 × 127.55 = 16.27 W

 

EXAMPLE 15: Three loads A, B and C are connected in parallel across a 250 V source. Load A takes 50 A. Load B is a resistor of 10 2 and load C takes 6.25 kW. Calculate (i) RA and Rc (ii) the currents Ig and Ic (iii) power in loads A and B (iv) total current (v) total power and (vi) total effective resistance.

Solution

 

EXAMPLE 16: Three resistors A, B and C connected in parallel take a total current of 12 A from the supply. IB = 21A and Ic=3.5 IB. If the total power taken is 3 kW, calculate (i) the current taken by the loads (ii) the individual resistance values (iii) the supply voltage and (iv) the individual powers.

Solution

 

EXAMPLE 17: Two 60 2 resistors are connected in series. If a resistor R is connected across one of them, the total circuit resistance becomes 80 2. Find the value of R.

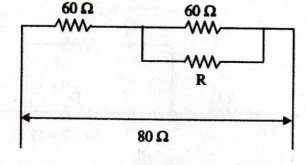
Solution

Total circuit resistance = 80 Ω

i.e., 80 = 60+ 60 Ω parallel with R or 80=  60 + 60 R / 60 + R

Therefore, 60 R / 60 + R = 80 - 60 = 20

R = 30 Ω

 

EXAMPLE 18: Determine the effective resistance between terminals A and B in the circuit of figure (a). If the current drawn at A is 9 A, find the current and the voltage drop across each element.

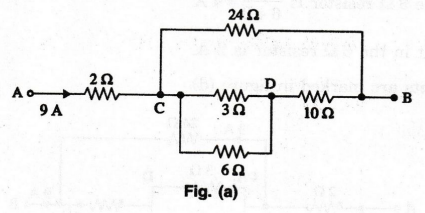
Solution

The parallel combination of 32 and 6 2 between C and D gives

= 3 × 6 / 3 + 6 = 2Ω

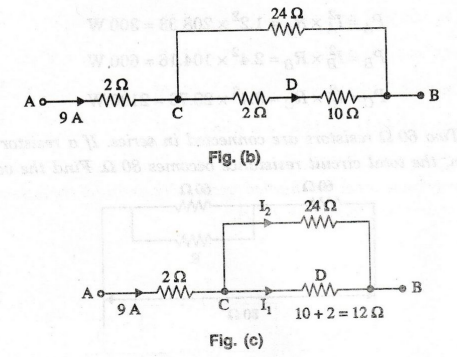
The circuit can be simplified as in figures (b) and (c). The current approaching the point C splits into two parts one along the 12 Ω resistor and the other along the 24 Ω resistor, both being in parallel. The currents I₁ and I₂ can be found out from current division rule.

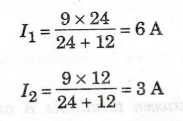
Referring to figure (a) the 6 A leaving point C splits like wise into 2 parts and the current through the 3 Ω resistor is 6 × 6 / 6 + 3 = 4 A

The current in the 6 Ω resistor is 2 A.

All the currents are marked in figure (d).

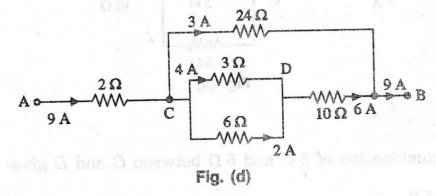
Voltage drop across 2 Ω resistor = 9 × 2 = 18 V

Voltage drop across 3 Ω resistor = 4 × 2 = 12 V

Voltage drop across 6 Ω resistor = 6 × 10 = 60 V

Voltage drop across 10 Ω resistor = 6 × 10 = 60 V

Voltage drop across 24 Ω resistor = 3 × 24 = 72 V

 

EXAMPLE 19: A 10 Ω resistor is connected in series with two 15 2 resistors connected is parallel. What resistance must be shunted across this parallel combination so that the total current taken from 20V supply is 1.5 A.

Solution

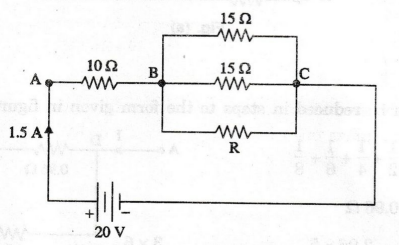
Let R be the resistance to be shunted across the parallel combination.

Voltage drop across AB = 1.5 × 10 = 15 V

Therefore, voltage drop across BC = 20 - 15 = 5 V

Current in each 15 Ω resistor = 5/15 = 1/3 A

1/3 A flows through each of 15 Ω resistor. The remaining current (i.e. 1.5 2 × 1/3) flows through R.

Current through R = 1.5-2/3=0.833 A

Voltage across R = 5 Volts

R = V / I = 5 / 0.8333 Ω

Therefore,

R = 6 Ω

 

EXAMPLE 20: If 20V is applied across AB, in the circuit of figure (a), calculate the total current, the power dissipated in each resistor and the value of the series resistance to halve the total current.

Solution

The circuit can be reduced in steps to the form given in figure (b).

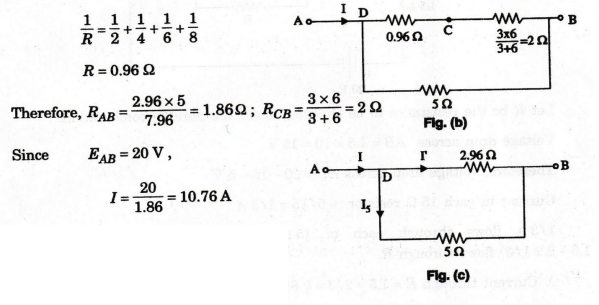
At D, this current splits, such that the current through the 5 Ω resistor is

If the total current were to be halved, the resistance RAB has to be doubled. Hence, the extra resistance to be added is the same as R_AB (i.e., 1.86 Ω ).

 

EXAMPLE 21: In the circuit of figure, it is given that the power consumed in the 6 Ω resistor is 24 W. Find the value of R.

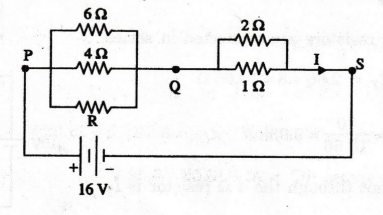
Solution

P = I² R

I = √P/R

Since power in the 6 2 resistor is 24 W, the current in it = √24/6 = 2 A

Voltage drop across PQ = 2 × 6 = 12 V

Therefore, voltage drop across QS = 16 - 12 = 4 V

Current I = V_QS / R_QS = ( 4 /  (2×1) / (2 + 1) ) = 6 A

Current through 4 Ω resistor = 12/4 = 3A

Therefore, current through R = 6 - (2 + 3) = 1A

R = V_PQ / I = 12 / I = 12 Ω

 

EXAMPLE 22: Find the current in 4 Ω  resistor.

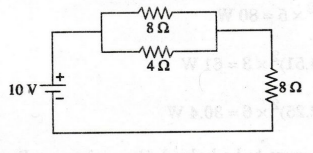
Solution

Here, 8 Ω and 4 Ω are connected in parallel.

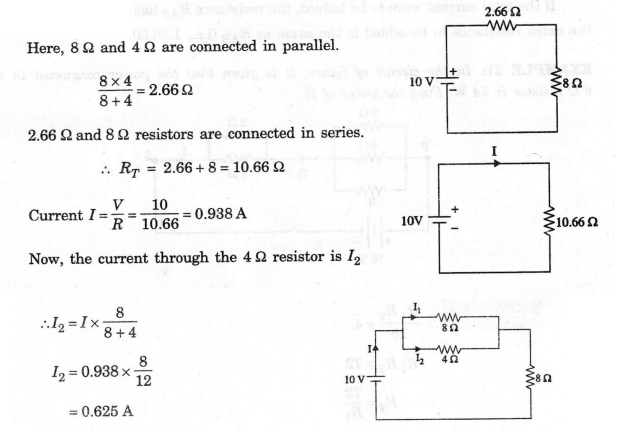
The current through 4 Ω resistor is 0.625A

 

EXAMPLE 23: Two resistors 4 Ω and 6 Ω are connected in parallel. If the total current is 12 A, find the current through each resistor.

Solution:

By using current division rule

I₁ = 7.2 A

I₂ = 4.8 A

 

EXAMPLE 24: Two coils connected in series have a resistance of 182 and when connected in parallel of 4 2. Find the value of resistance of the two coils. (AU/ECE - May 2005)

Solution:

Let R₁, R₂ be the resistance of the coils.

Given R₁ + R₂ = 18 Ω &

R₁  R₂ / R₁ + R₂  = 4Ω

R₁ = 12 Ω , R₂ = 6 Ω

 

EXAMPLE 25: The element of 500 W electric iron is designed for use on a 200 V supply. What value of resistance is needed to be connected in series in order that iron can be operated from 240 V supply.

Solution

Resistance of electric iron R = V² / P = 200² / 500 = 80 Ω

Now, this electric iron is to be operated from 240V and a resistance is connected in series with electric iron.

From this circuit,

I = P / V = 500 / 200 = 2.5 A

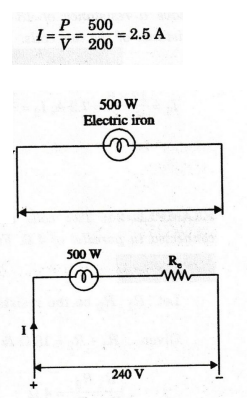
Since voltage drop across the lamp is 200 V, voltage to be dropped in the series resistor = 240 - 200 = 40 V

The value of the resistor R_e = 40 / 2.5 = 16 Ω

R_e = 16 Ω

 

EXAMPLE 26: Two resistors R₁ = 40 Ω and R₂ = 25 Ω are connected in parallel across 20 V DC supply. Find the total power dissipated in the circuit.

Solution

 

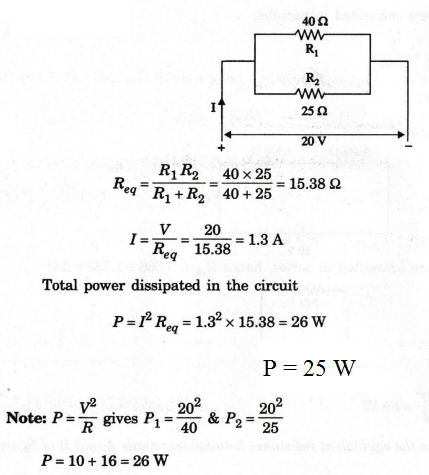
EXAMPLE 27: Calculate the total power supplied by the battery in the network shown in figure.

Solutuion

 

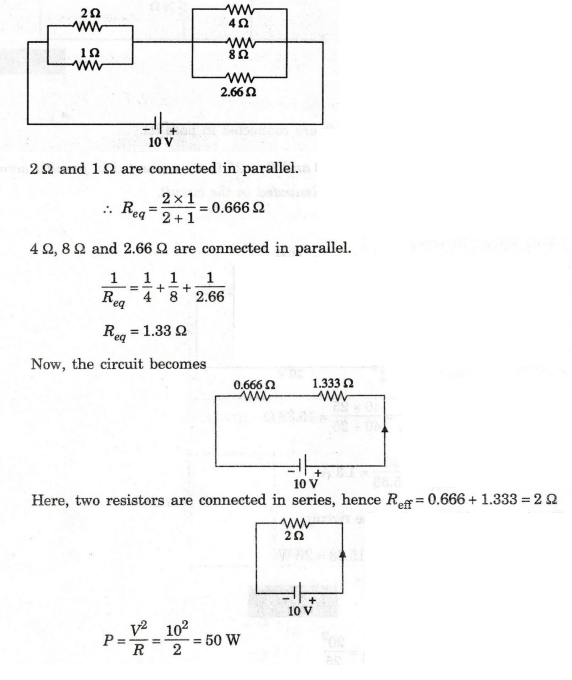
EXAMPLE 28: Determine the equivalent resistance between terminals A and B of figure shown below.

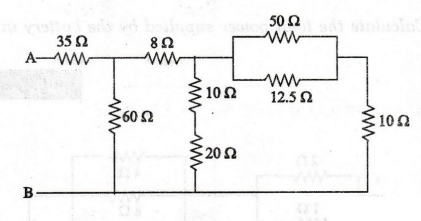
Solution

50 Ω and 12. 5 Ω are connected in parallel.

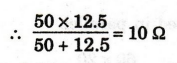
10 Ω and 20 are connected in series, 10 + 20 = 30 Ω

Now, circuit becomes

10 Ω and 10 Ω are connected in series 10 + 10 = 20 Ω

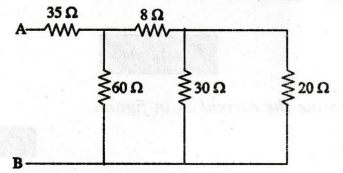
30 and 20 Ω are connected in parallel.

8 Ω and 12 Ω are connected in series 8+12=20 Ω

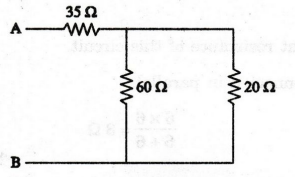
60 Ω and 20 Ω are connected in parallel.

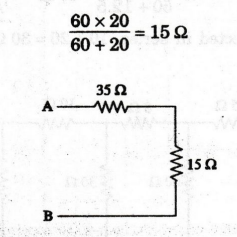
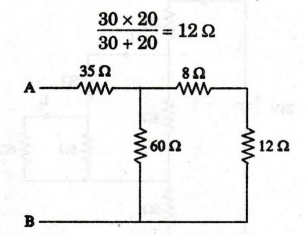
35 Ω and 15 Ω are connected in series.

R_AB = 35 + 15 = 50 Ω

R_AB = 50 Ω

 

EXAMPLE 29: Determine the current I₃ in figure.

Solution

First find equivalent resistance of this circuit.

6 Ω and 6 Ω  are connected in parallel.

6 × 6 / 6 + 6 = 3 Ω

EXAMPLE 30: What is the potential across 5 Ω resistor in the circuit?

Solution

Here, three resistors are connected in series,

R_eq = 3+5+2=10 Ω

I = V / R_eq = 10 / 10 = 1 A

Voltage across 5 Ω = IR = 1 × 5 = 5 V

 

EXAMPLE 31: For the circuit shown in figure, calculate equivalent resistance of the circuit and the total circuit current.

Solution

4 Ω, 5 Ω and 6 Ω are connected in series.

 

EXAMPLE 32: Determine the total current taken from the source. (MKU/I YEAR - Apr 2002)

Solution

50 Ω and 50 Ω are connected in series

Hence, 50 + 50 = 100

100 Ω and 100 Ω are connected in series

So, 100 + 100 = 200 Ω

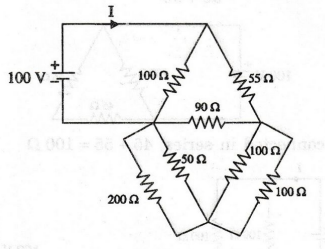
100 Ω and 100 Ω are connected in parallel

(100 × 100 / 100 + 100) = 50 Ω

200 Ω and 50 Ω are connected in parallel

Hence, (200 × 50 / 200 + 50) = 40 Ω

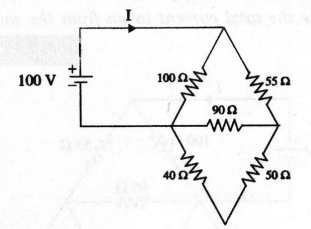
40 Ω and 50 Ω are connected in series, 40 + 50 = 90 Ω

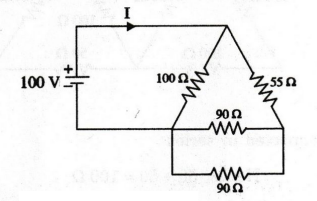
90 Ω and 90 Ω  are connected in parallel.

90 × 90 / 90 + 90 = 45 Ω

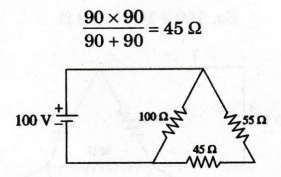
45 Ω and 55 Ω are connected in series, 45 + 55= 100 Ω

 

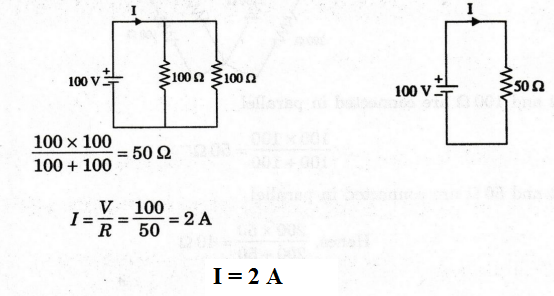
EXAMPLE 33: For the circuit shown in figure, the power consumed by 62 resistor is 150 W. Find the supply voltage.

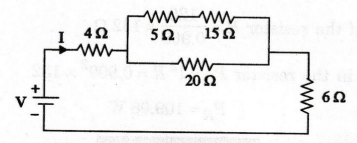
Solution

Power consumed by 6 Ω resistor 150 W

Current flow through 6 Ω resistor I = √P/R = √150/6 = 5A

Current supplied by the battery is also 5 A.

Input voltage V = I R_eq

 

EXAMPLE 34: A filament lamp is rated for 100 W, 110 V. Find the value of the resistance to be connected in series with this lamp so that it can be operated on a 230 V supply. What is the power loss in the resistor?

Solution

Current in the lamp I = P / V = 100 / 110 = 0.909 A

Since voltage drop across the lamp is 110 V, voltage to be dropped in the series resistor = 230 - 110 = 120 V

Therefore value of the resistor R = 120 / 0.909 = 132 Ω

Power dissipated in the resistor P_R = I² R = 0.909² × 132

P_R = 109.06 W

P_R = 109.08 W

 

EXAMPLE 35: When a resistor is placed across a 230 V supply, the current is 12 A. What is the value of the resistor that must be placed in parallel to increase the load current to 16 A.

Solution

 

EXAMPLE 36: Find (i) Current in 15 Ω resistor, (ii) Voltage across 18 Ω resistor, (iii) Power dissipated in 7 Ω resistor in the circuit shown below.

(AW/Mech - Dec 2005)

Solution:

(i) Current through 15 Ω resistor

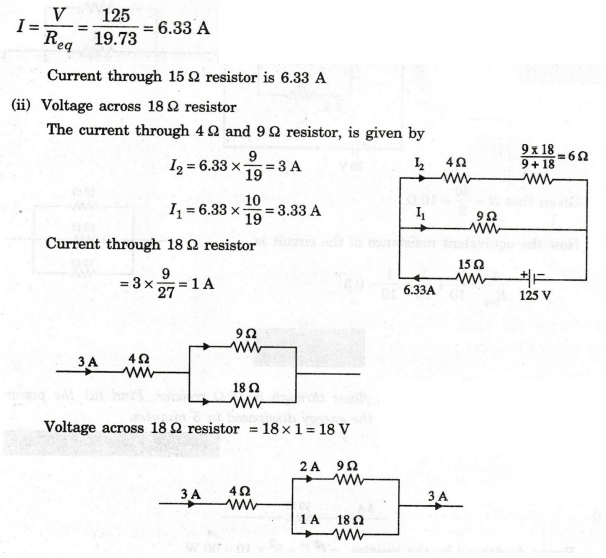
(iii) Power dissipated in the 7 Ω resistor

Current through 2 Ω and 7 Ω resistor is 3.33 A

Therefore, power dissipated in the 72 resistor = 3.33² ×7 = 77.62 W

 

EXAMPLE 37: Three resistors of equal resistances are connected in parallel across a 20 V de source. If the current through one of the resistors is 2 A, what is the value of equivalent resistance of the parallel connected resistors.

Solution

R_eq = 3.33 Ω

 

EXAMPLE 38: A current of 3A flows through a 10 2 resistor. Find (a) the power dissipated by the resistor and (b) the energy dissipated in 5 minutes.

Solution

Power dissipated by the resistor =I² R = 3² × 10 = 90 W

(b) Energy dissipated in 5 minutes

5 minutes = 5 × 60 = 300 second

Energy = Power × time = 90 × 300 = 27000 W- second

 

EXAMPLE 39: Find the supply voltage E such that the power in the 20 resistor is 180 W.

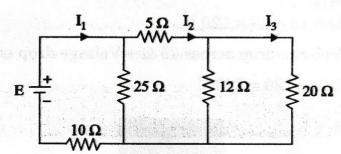
Solution

Power in the 20 Ω resistor = 180 W

Current through 20 Ω resistor (I₃) is given by

I²₃ R=180

I₃ = √180 / 20 = 3A

Voltage across 20 Ω resistor = I₃ R = 3 × 20 = 60 V

This 60 V is applied across 12Ω resistor.

Therefore, the current flow through 12 Ω resistor = 60 / 12 = 5A

I₂ = 5 + 3 = 8 A

Voltage drop across 5 Ω resistor = 5 × 8 = 40 V

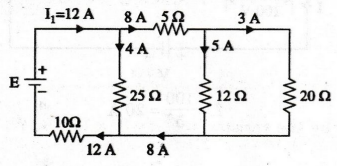
Voltage drop across 25 Ω resistor

= Voltage drop across 5Ω + Voltage drop across 12 Ω

= 40 + 60 = 100 V

Current through 25 Ω resistor = 100 / 25 = 4A

I₁ = 4 + 8 = 12A

Current through 10 Ω resistor = 12 A

Voltage across 10 Ω = 12 × 10 = 120 V

Input voltage E = Voltage drop across 25 Ω + Voltage drop across 10 Ω

= 100 + 120 = 220 V

E = 220 V

 

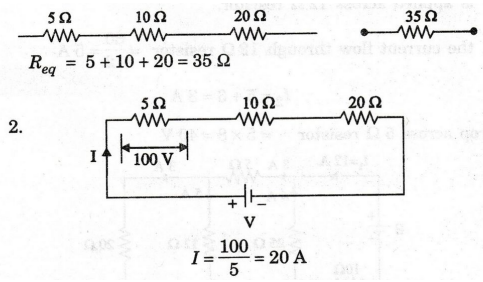
EXAMPLE 40: For the circuit shown in figure, (1) find the equivalent resistance across the supply. (2) if the voltage drop across 5 Ω is 100 V, find the supply voltage (3) find the power consumed by each resistor.

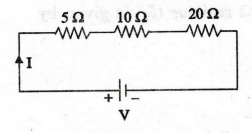
Solution

1. Equivalent resistance of the circuit is

Voltage drop across 10 Ω = 20 × 10 = 200 V

Voltage drop across 20 Ω = 20 × 20 = 400 V

Supply voltage = 100 + 200 + 400 = 700 V

V = 700 V

3. Power consumed by 5 Ω resistor = I² R = 20² × 5 = 2000 W

Power consumed by 10 Ω resistor = 20² × 10 = 4000 W

Power consumed by 20 Ω resistor = 20² × 20 = 8000 W

 

EXAMPLE 41: Find the voltage between A and B in a voltage divider network shown in figure.

Solution:

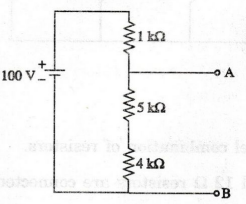
Equivalent resistance R_eq = 1 k Ω + 5k Ω + 4k Ω = 10 k Ω

Current in the circuit I = V / R_eq = 100 / 10 k Ω = 0.01 A

Voltage drop across AB = 0.01 × 9kΩ = 90 V

 

EXAMPLE 42: Find the current through 10 2 resistor for the following circuit.

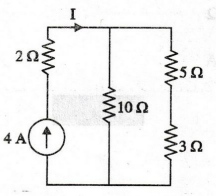
Solution

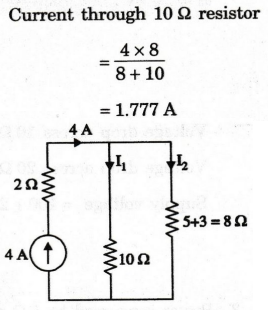
I₁₀ Ω = 1.777A

 

EXAMPLE 43: Find the current supplied by the 60 V source in the network.

Solution

First reduce the parallel combination of resistors.

 

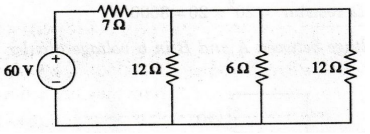
EXAMPLE 44: If R_eq = 50 Ω in the circuit shown in figure, find the value of R.

Solution

Three 12 Ω resistors are connected in parallel. Now they are reduced to

 

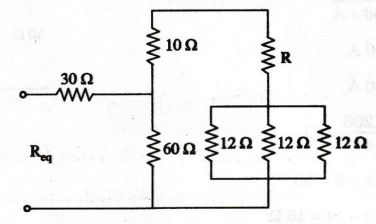
EXAMPLE 45: Find resistance across AB.

Solution

4 Ω and 6 Ω are connected in parallel.

Resistance across AB = 10.05Ω

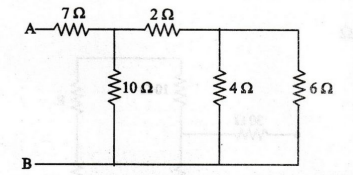
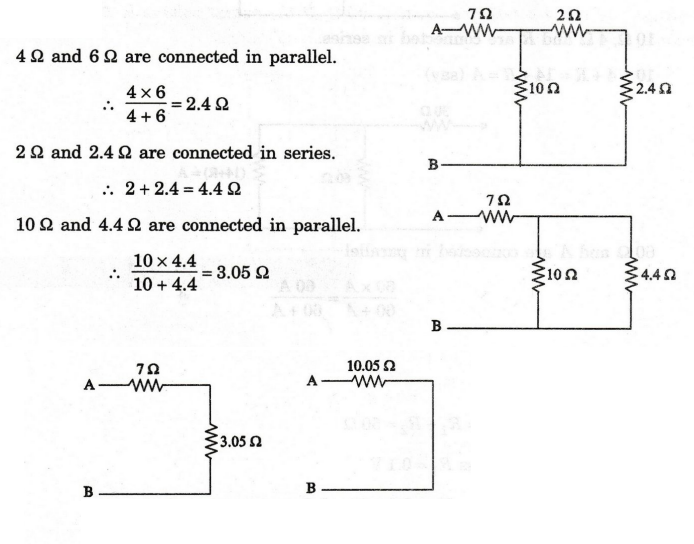
EXAMPLE 46: What is the value of R₁, to divide the current as shown in circuit.

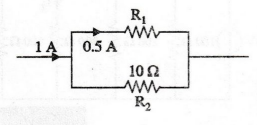
Solution

Current through 10 Ω resistor is 0.5 A.

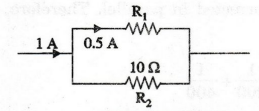
Therefore the resistance R₁ = 10Ω

 

EXAMPLE 47: A voltage divider circuit of two resistors is designed with a total resistance of the two resistors equal to 50 2. If the output voltage is 10% of the input voltage, obtain the values of the two resistors in the circuit.

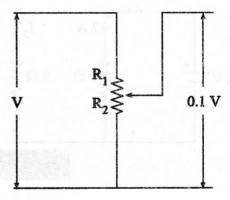
Solution

 

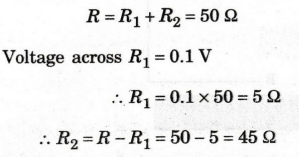
EXAMPLE 48: In figure, apply current divider rule to find I3.

Solution

Here, 4 resistors are corrected in parallel. Therefore, the equivalent resistance is except 300 Ω

 

EXAMPLE 49: Apply Ohms law in the circuit given in figure to find V and I₂

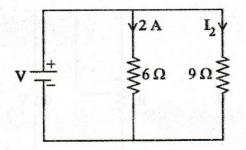
Solution:

Voltage drop in 6Ω IR = 2 × 6 = 12 V

Supply voltage V = 12 V

Current through 9Ω, I₂ = V / R₂ = 12 / 9 = 1.33 A

I₂ = 1.33 A

 

EXAMPLE 50: The resistances of 1.5 2 and 3.5 2 are connected in parallel and this parallel combination is connected in series with a resistance of 1.95 2. Calculate the equivalent resistance value. (AU, Trichy/EEE - June 2009)

Solution

 

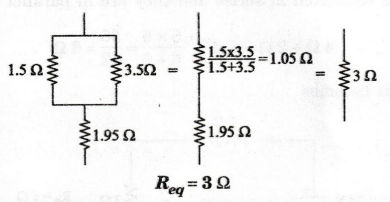
EXAMPLE 51: Find the current, I supplied by the source in the following circuit.

Solution

2 Ω and 4 Ω are connected in series

2 + 4 = 6Ω

6Ω and 3 Ω are connected in parallel

6 × 3 / 6 + 3 = 2 Ω

4Ω and 4Ω are connected in parallel

→ 4 × 4 /  4 + 4 = 2 Ω

Now, the circuit becomes

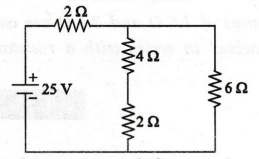
4 Ω and 2Ω are connected in series and they are in parallel with 6 Ω resistor.

4 Ω + 2 Ω = 6Ω

6 × 6 / 6 + 6 = 36 / 12 = 3 Ω

Now, the circuit becomes

Current supplied by source I = 25 / 2 + 3 = 25 / 5 = 5A

I = 5 A

 

EXAMPLE 52: Determine the current I delivered by the source.

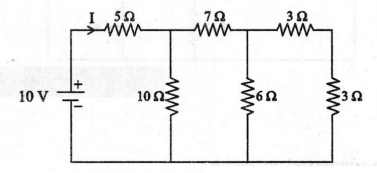
Solution

3 Ω and 3 Ω are connected in series

3 + 3 = 6Ω

Now, the circuit becomes

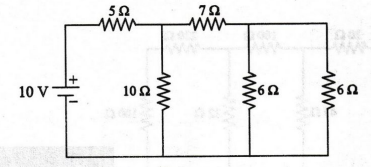
6 Ω and 6 Ω are connected in parallel

6 × 6 / 6 + 6 = 3 Ω

Now, the circuit becomes

 

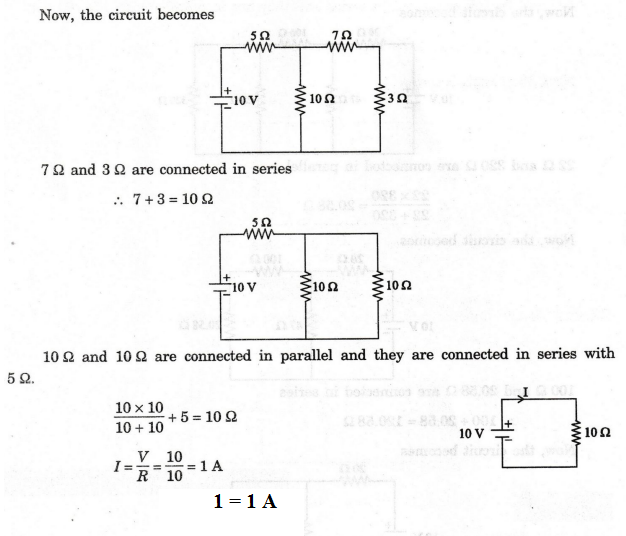
EXAMPLE 53: Find the current supplied by 10 V source shown in figure using resistor reduction.

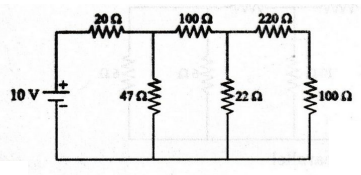
Solution

220 and 100 Ω are connected in series. i.e 220 + 100 = 320 Ω

Now, the circuit becomes

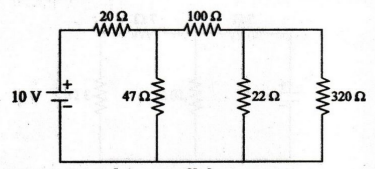
22 and 320 Ω are connected in parallel

100 Ω and 20.58 Ω are connected in series

100 + 20.58 = 120.58 Ω

Now, the circuit becomes

47 Ω and 120.58 Ω are connected in parallel

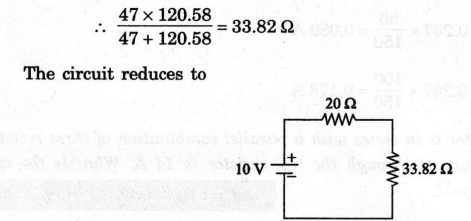
Here, 20 Ω and 33.82 Ω are connected in series

20 + 33.82 = 53.82 Ω

Current I = 10 / 53.82 = 0.185 A

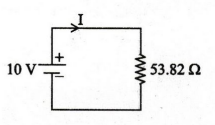
I = 0.185 A

 

EXAMPLE 54: Calculate the current through 50 2 and 100 resistors in the circuit shown below.

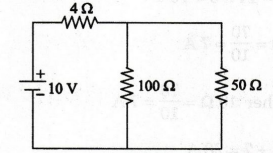
Solution

First find the total resistance of the circuit

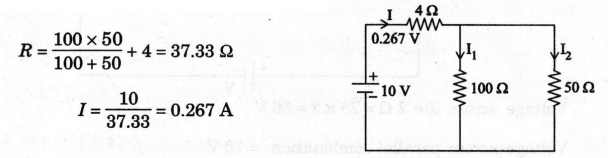
By using current division rule,

 

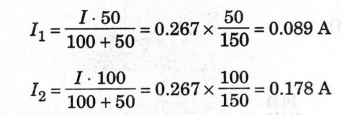
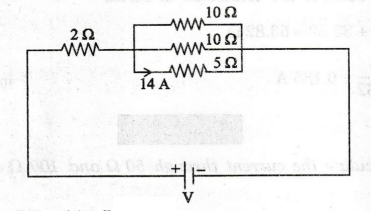
EXAMPLE 55: A 2 2 resistor is in series with a parallel combination of three resistors 102, 10 2 and 5 2. If the current through the 5 2 resistor is 14 A. What is the total voltage across the entire circuit? (AU, Trichy/EEE - May 2009)

Solution

Voltage across 5 Ω = 14 × 5 = 70 V

Current through 10 Ω = 70 / 10 = 7 A

Current through another 10 Ω = 70 / 10 = 7A

Total current = 14 + 7 + 7 = 28 A

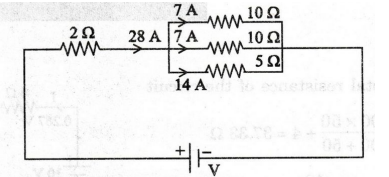
Voltage across the 2 Ω = 28 × 2 = 56 V

Voltage across parallel combination = 70 V

Total voltage V = 56 + 70 = 126 V

V = 126 V