Discrete random variable: Formula, Solved Example Problems

FORMULA

Note :

1. Prove that E(ax + b) = a E(X) + b.

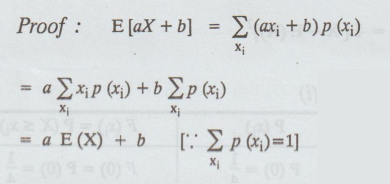
2. If X is a random variable then show that Var(aX+b) = a² Var (X)

Proof :

Let Y = aX + b

E(Y) = E[aX + b]

We know that, E[aX + b] = a E[X] + b

Y - E(Y) = (ax + b) - a E(X) – b

Y - E(Y) = aX - aE(X)

Y - E(Y) = a [X - E(X)]

 [Y - E(Y)]2 = a² [X - E (X)]²

Var(Y) = a2 Var(X)

i.e., Var(ax + b.) = a² Var(X)

3. P[X = x_i] = p(x)

→ Probability function (or) Probability distribution (or) p.m.f (probability mass function)

4. f (x) → p.d.f (probability density function)  (or) density function.

5. F(x) → c.d.f (cumulative distribution function) (or) distribution function.

 

Problems under the distribution function for discrete random variable

Example 1.4.1

 [Given P (xi) to find F (xi) type]

For the following probability distribution (i) Find the distribution function of X. (ii) What is the smallest value of x for which P(X ≤ x) > 0.5

Solution: (i)

(ii) The smallest value of x for which P (X ≤ x;) > 0.5 is 1.

Note : The smallest value of x for which P (X ≤ x) > 0.1 is 0 and

The smallest value of x for which P (X ≤ x;) > 0.8 is 2.

 

Example 1.4.2

[Given F (x_i) to find P (x_i) type]

Obtain the probability function (or) probability distribution from the following distribution function.

Solution :

To Find P(x_i)

 

Example 1.4.3

The number of hardware failures of a computer system in a week of operations has the following pmf: [A.U. M/J 2006]

Find the mean of the number of failures in a week.

Solution :

 

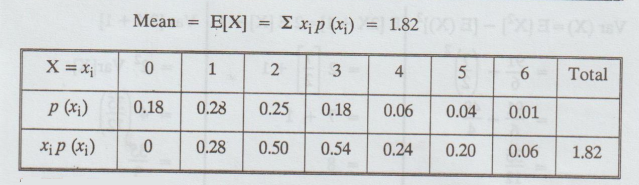
Example 1.4.4

Determine the mean, variance, E[(2X+1)], Var(2X+1) of a discrete random variable X given its distribution as follows:

Solution :

 

Example 1.4.5

The monthly demand for Allwyn watches is known to have the following probability distribution.

Determine the expected demand for watches. Also compute the variance. [A.U. N/D 2006]

Solution :

Let X denote the demand

 

Example 1.4.6

When a die is thrown, X denotes the number that turns up. Find E (X), E (X2) and var (X²). [A.U. M/J 2006, A.U N/D 2019 (R17) PS]

Solution : X is a discrete random variable taking values, 1, 2, 3, 4, 5, 6 and with probability for each

 

Example 1.4.7

Determine the constant K given the following probability distribution of discrete random variable X. Also find mean and Variance of X.

 

Example 1.4.8

If X has the distribution function

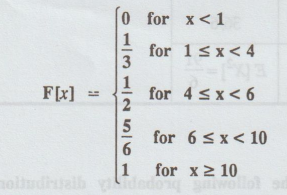
Find

(1) The probability distribution of X.

 (2) P (2 < X < 6)

 (3) Mean of X

(4) Variance of X.

[A.U. A/M. 2008]

Solution:

(1) The probability distribution of X.

 

Example 1.4.9

A random variable X has the following probability distribution.

 [A.U. N/D 2007, M/J 2009, A.U CBT M/J 2010] [A.U N/D 2011]

Find

(1) The value of k,

(2) Evaluate P(X < 2) and P(-2 < X < 2)

(3) Find the cumulative distribution of X and

(4) Evaluate the mean of X.

Solution :

 

Example 1.4.10

A discrete random variable X has the following probability distribution.

[A.U CBT N/D 2011, Trichy M/J 2011]

(i) Find the value of a.

(ii) Find P(X < 3), P(0 < x < 3), P(X ≥ 3)

(iii) Find the distribution function of X.

Solution :

 

Example 1.4.11

A random variable X has the following probability function:

 (a) Find K     [A.U N/D 2010, M/J 2012, M//J 2014] [A.U A/M 2015 R-8]

(b) Evaluate P[ X < 6], P[ X ≥ 6]

 (c) If P [ X ≤ C ] > 1/2, then find the minimum value of C.

(d) Evaluate P [1.5 < X < 4.5/X > 2]

(e) Find P [X < 2], P[X > 3], P[1 < X < 5]

[A.U M/J 2007, N/D 2008] [A.U. Tvli A/M 2009]

Solution: (a) We know that, 

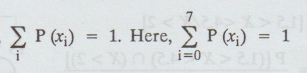
i.e., 0 + K + 2K + 2K + 3K + K² + 2K² + 7K² + K = 1

i.e.,10 K² + 9K – 1 = 0

= K= -1 or K = 1/10

Since, P(X) ≥ 0 the value K = -1 is not permissible

Hence, we have K = 1/10

 (b) (i) P[X ≥ 6] = P[X = 6] + P [X = 7]

= 2/100 + 17/100 = 19/100

 (ii) P(X < 6] = 1- P [X ≥6]

=  1- 19/100 = 81/100

 (c)

The minimum value of C = 4. [ P [ X ≤ C ]> 1/2]

 (d) P [1.5 < X < 4.5/X > 2]

= P[2 < X < 4.5] / 1 – P (X ≤ 2]

= P(3) + P(4) / 1- [P (0) + P(1) + P (2)]

= 2 /10 + 3/10 / 1- [0 + 1/10 + 2/10 ] = 5/10 / 1- 3/10 = 5/10/ 71/0 = 5/7

 (e) (i) P (X < 2) P [X=0] + P(X = 1] = 0+ K = K = 1/10

(ii) P (X > 3) = 1 - P(X ≤ 3)

=1- [P (X = 0) + P (X = 1) + P (X = 2) + P (X = 3)]

= 1- [0 + K + 2K + 2K]

= 1- 5K = 1- 5/10 = 1 – ½ = 1/2

 (iii) P (1 < X < 5) = P (X = 2) + P(X = 3) + P(X = 4)

 = 2K + 2K +  3K = 7K = 7/10

 

Example 1.4.12

A random variable 'X' has the following probability function :

Find k, P [X3] and P (0 < x < 4) [A.U. Tvli. A/M 2009]

Solution : (i) We know that,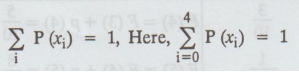 

 (i.e.,) k + 3k + 5k + 7k + 9k = 1

25 k = 1 ⇒ k = 1/25

 (ii) P (X ≥ 3) = P (X = 3) + P (X = 4)

= 7k + 9k = 16 k = 16 (1/25) = 16/25

 (iii) P (0 <X< +) = P(X = 1) + P (X = 2) + P(X = 3)

= 3k+ 5k + 7k = 15k

= 15 (1/25) = 3/5

 

Example 1.4.13

Let X be a random variable such that P (X = -2) = P (X = -1) = P (X = 1) = P (X = 2) and P (X < 0) = P(X = 0) = P (X>0). Determine the probability mass function and the distribution of X. [AU N/D 2006]

Solution : Given:

P [X < 0]  = P[X = 0] = P [X > 0]X... (1)

P [X = -2] = P[X=1] = P [X = 1] = P [X = 2] ... (2)

Let P [X = -2] =  P [X = -1] = P [X = 1] = P [X = 2] = a

We know that,

P[X < 0] = P [X = -2] + P [X = -1] = a + a = 2a

 (1) => P [X < 0] = P [X = 0] = P [X > 0] = 2a

 

Example 1.4.14

If the random variable X takes the values 1, 2, 3 and 4 such that 2P (X  = 1) = 3P (X = 2) = P (X = 3) = 5P (X = 4) find the probability  distribution and cumulative distribution function of X.

 [A.U CBT A/M 2011, A.U N/D 2012, A.U A/M 2017 R8] [A.U A/M 2019 (R13) PQT] [A.U A/M 2015 (RP) R8]

Solution: X is a discrete random variable, doue sidshay

Given : 2P [X = 1] = 3P [X = 2] = P [X=3] = 5P [X = 4]

Let 2P [X = 1] = 3P (X = 2] = P(X = 3] = 5P (X = 4] [X = 2]  = k ....(1)

We know that,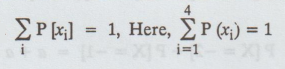 

i.e., k/2 + k/3 + k + k/5 =1

61/30k = 1 ⇒ k = 30/61

Example 1.4.15

The probability function of an infinite discrete distribution is given by P[X = j] =1/2^j , j = 1, 2, ∞. Find the mean and variance of the distribution. Also find P[X is even], P [X≥ 5] and P[X is divisible by 3]. [A.U. N/D 2006] [A.U N/D 2011]

Solution: Given: P[ X = j] = 1/2^j = (1/2)^j

FORMULA (1-x)^-2 = 1 = 2x = 3x² + ...

(1-x)^-3 = ½ [ 1.2 + 2.3x+ 3.4x² + ...]

Variance of X = Var(X) = E [X²] - [E[X]]²

= 6 - (2)² = 6 - 4 = 2

(1) P[X is even] =  P[X 2] + P(X = 4] + ...

= (1/2)² + ( ½)⁴ + (1/2)⁶ +....

= ¼ + (1/4)² + (1/4)³ +....

= ( 1 – x )^-1 - 1 , Here , x = ¼ [ (1 - x)^-1 = 1 + x + x² +....]

= (1-1/4)^-1 – 1 = (3/4)^-1 -1 =  4/3 -1 = 1/3

 (2) P [X ≥ 5] = P(X = 5] + P (X = 6] + ...

= (1/2)⁵ + (1/2)⁶+....

= (1/2)⁵ [ 1 + (1/2) + (1/2)² + ....]

= (1/2)⁵ [1 – x ]^-1 Here x= 1/2

= (1/2)⁵ [1- 1/2]^-1 = (1/2)⁵ (1/2)^-1 = 1/2⁴ = 1/16

 (3) P[X is divisible by 3] (or) P[X is multiple of 3]

= P [X = 3] + P [X = 6] +....

= (1/2)³ +(1/2)⁶ + (1/2)⁹ +....

= 1/8 + (1/8)² + (1/8)³ +....

= ( 1 – x )^-1 -1 , Here x = 1/8

= (1 - 1/8)^-1 -1 = (7/8)^-1 = 8/7 -1= 1/7

 

Example 1.4.16

If Var(X) = 4, then find Var( 3X + 8), where X is a random variable. [A.U, Model] [A.U Tvli M/J 2011]

Solution : We know that, Var(ax + b) =a² Var(X)

Var(3X + 8) = 3² Var(X)

= 3² [4] = 36

 

Example 1.4.17

Let X be a Random Variable with E(X) = 1 and E [X (X-1)] = 4. Find Var X and Var (2-3X), Var [X/2] [A.U. May, 2000], [A.U. A/M. 2008]

Solution:

Given: E(X) = 1,  E[X (X-1)] = 4

E[X (X-1)] = E (X² - X] = E[X²] - E[X]

4 = E(X²) - 1

E (X²) = 4 + 1 = 5

Var X = E (X²) - [E(X)]²

= 5 - 1 = 4

Var (2 - 3X) = (-3)² Var X  [ Var ( aX±b) = a² Var X ]

= 9 (4) = 36

Var [X/2] = (1/2)² = ¼ [4] = 1

 

Example 1.4.18.

If the probability mass function of a r.v. X is given by P (X = r) = kr³, r = 1, 2, 3, 4 find

(i) the value of k,

 (ii) the mean and variance of X and X [A.U. A/M 2015 (RP) R13]

(iii) the distribution function of X

(iv) P ( ½ < X < 5/2 / X > 1)  [A.U Tvli. M/J 2010]

Solution :

 (i) We know that, 

 (ii) & (iii) Given: P (X = r) = kr³, r = 1, 2, 3, 4

E [X] = Σx_i p (x_i)  =  3.54/100 = 3.54

E [X²] = Σx_i² p (x_i) = (1300) (1/100) = 13

Var(X)  = E (X²) - [E (X)]²

= 13 [3.54]² = 13 - 12.5316 = 0.4684