Divergence

Divergence

 AU : May-04, 06, 16,18, Dec.-04, 07, 10, 13, 14,18

• It is seen that 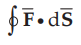gives the flux flowing across the surface S. Then mathematically divergence is defined as the net outward flow of the flux per unit volume over a closed incremental surface. It is denoted as div   and given by,

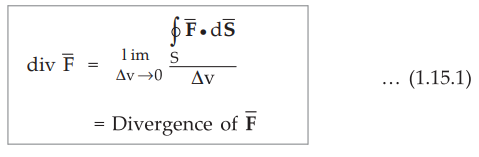
where Δv = Differential volume element

Key Point : Divergence of vector field   at a point P is the outward flux per unit volume as the volume shrinks about point P i.e. lim Δv ^0 representing differential volume element at point P.

• Symbolically it is denoted as,

• Similarly divergence in other co-ordinate systems are,

• Physically divergence at a point indicate how much that vector field diverges from that point.

• Consider a solenoid i.e. electromagnet obtained by winding a coil around the core. When current passes through it, flux is produced around it. Such a flux completes a closed path through the solenoid hence solenoidal field does not diverge. Thus mathematically, the vector field having its divergence zero is called solenoidal field.

1. Physical Meaning of Divergence

• Let  be the flux density vector then, the divergence of the vector flux density  is the outflow of flux from a small closed surface per unit volume as the volume shrinks to zero.

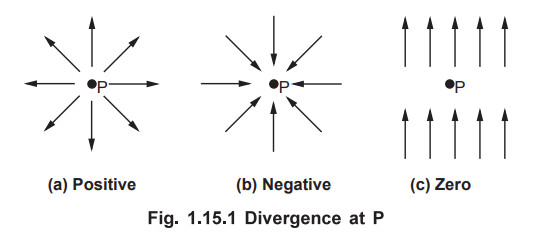
• The divergence of  at a given point is a measure of how much the field represented by  diverges or converges from that point. If the field is diverging at point P of vector field  as shown in the Fig. 1.15.1 (a), then divergence of  at point P is positive. The field is spreading out from point P. If the field is converging at the point P as shown in the Fig. 1.15.1 (b), then the divergence of  at the point P is negative. It is practically a convergence i.e. negative of divergence. If the field at point P is as shown in the Fig. 1.15.1 (c), so whatever field is converging, same is diverging then the divergence of  at point P is zero.

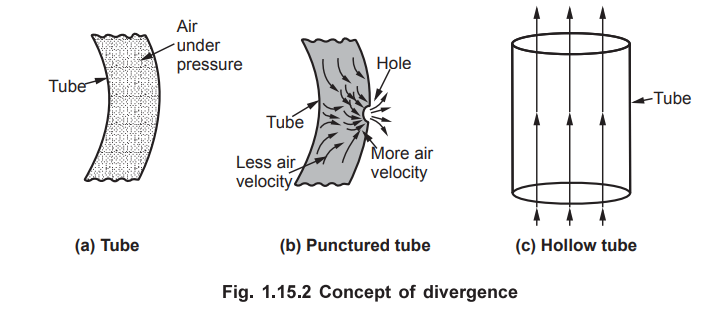
• Practically consider a tube of a vehicle in which air is filled at a pressure. If it is punctured, then air inside tries to rush out from a tube through a small hole. Thus the velocity of air at the hole is greatest while away from the hole it is less. If now any closed surface is considered inside the tube, at one end velocity field is less while from other end it has higher value, as air rushes towards the hole. Hence the divergence of such velocity inside is positive. This is shown in the Fig. 1.15.2 (a) and (b).

• As seen from the Fig. 1.15.2 (b), the air velocity is a function of distance and hence divergence of velocity is positive. The density of lines near hole is high showing higher air velocity. The source of such velocity lines is throughout the tube and hence anywhere inside the tube, at any point the divergence is positive.

• If there is a hollow tube open from both ends then air enters from one end and passes through the tube and leaves from other end. This is shown in the Fig. 1.15.2 (c). The velocity of air is constant everywhere inside the tube. In such a case the divergence of the velocity field is zero, inside the tube

.• A positive divergence for any vector quantity indicates a source of that vector quantity at that point. A negative divergence for any vector quantity indicates a sink of that vector quantity at that point. A zero divergence indicates there is no source or sink exists at that point.

• In short, if more lines enter a small volume than the lines leaving it, there is positive divergence. If more lines leave a small volume than the lines entering it, there is negative divergence. If the same number of lines enter and leave a small volume, the field has zero divergence. Note that the volume must be infinitesimally small, shrinking to zero at that point, where divergence is obtained.

• As the result of divergence of a vector field is a scalar, the divergence indicates how much flux lines are leaving a small volume, per unit volume and there is no direction associated with the divergence.

2. Properties of Divergence of Vector Field

• The various properties of divergence of a vector field are,

1. The divergence produces a scalar field as the dot product is involved in the operation. The result does not have direction associated with it.

2. The divergence of a scalar has no meaning. Thus if m is a scalar field then m has no meaning. Note that  operator can operate on scalar field but dot product i.e. divergence of a scalar has no meaning.

3. 

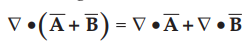
Ex. 1.15.1 Determine the divergence of these vector fields.

AU: Dec.-07, Marks 10, Dec.-13, Marks 8

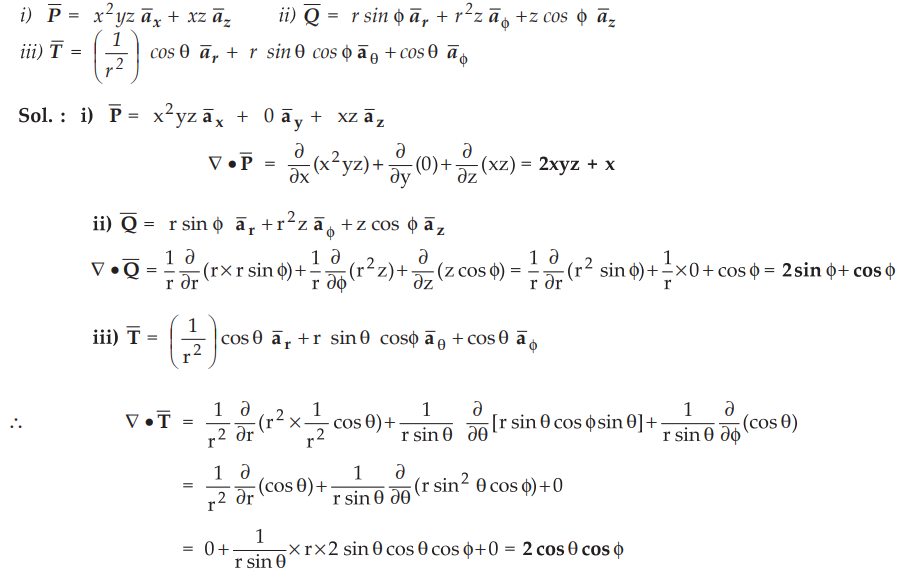
Ex. 1.15.2 Determine the constant c such that 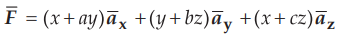 will be solenoidal. AU : May-06, Marks 6

Sol. : For a field to be a solenoidal,

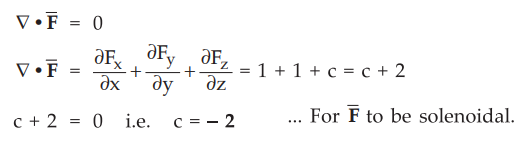
Examples for Practice

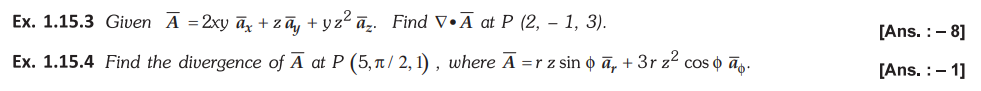
Review Questions

1. Write note on divergence. AU: Dec.-04, 10, 13, 14, May-04, 16,18, Marks 4

2. Write the expression for divergence in three co-ordinates systems. AU: Dec.-18, Marks 3