Divergence Theorem

Divergence Theorem

AU : May-04, 07, 09, 19, Dec.-09, 14, 15, 17, 18, 19

• It is known that,

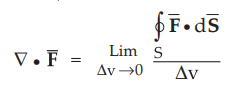... Definition of divergence

• From this definition it can be written that,

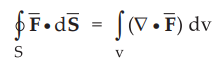 ...(1.16.1)

• This eqution (1.16.1) is known as divergence theorem or Gauss-Ostrogradsky theorem.

• The Divergence theorem states that,

The integral of the normal component of any vector field over a closed surface is equal to the integral of the divergence of this vector field throughout the volume enclosed by that closed surface.

• The theorem can be applied to any vector field but partial derivatives of that vector field must exist. The divergence theorem as applied to the flux density. Both sides of the divergence theorem give the net charge enclosed by the closed surface i.e. net flux crossing the closed surface.

Key Point : The divergence theorem converts the surface integral into a volume integral, provided that the closed surface encloses certain volume. 

• This is advantageous in electromagnetic theory as volume integrals are more easy to evaluate than the surface integrals.

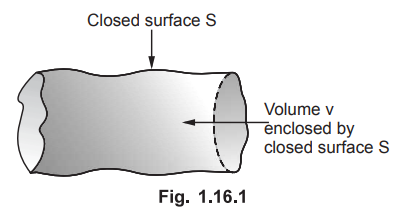
• The Fig. 1.16.1 shows how closed surface S encloses a volume v for which divergence theorem is applicable.

Key Point : The divergence theorem as applied with Gauss's law is included in the section 3.10 of chapter 3.

Ex. 1.16.1 Calculate the flux of the vector field 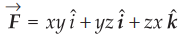 over the surface of a unit cube whose edges are parallel to the axes and one of the comers is at the origin. Use this result to illustrate the divergence theorem. AU : Dec.-19, May-04, 07, 09, Marks 13

Sol . : 

Ex. 1.16.2 Using Divergence theorem, evaluate 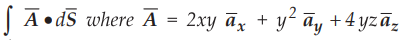 and S is the surface of the cube bounded by x = 0, x = 1; y = 0, y = 1; and z = 0, z = 1. AU : Dec.-09, Marks 6

Sol. : 

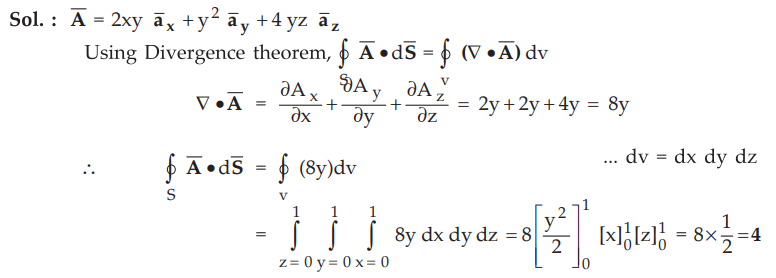
Ex. 1.16.3 i0 Verify the divergence theorem for a vector field 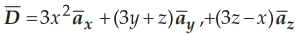 in the region bounded by the cylinder x² + y² = 0 and the planes x = 0, y = 0 and z = 2. AU: Dec.-15, Marks 12

Ans. :

Ex. 1.16.4 Verify the divergence theorem for the function 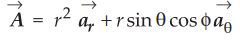 over the surface of a quarter of a hemisphere defined by 0 < r < 3. 0 < θ <π/2, 0 < ϕ <π/2. AU : Dec.-18, Marks 15

Sol. : According to Divergence theorem,

Review Question

1. State and explain the divergence theorem. AU : Dec.-08,14,17 May-07,09,19, Marks 6