Divergence Theorem

Divergence Theorem

AU : Dec.-03, 05, 08, 11,12. 14, 16, May-04, 06. 07, 08, 12, 17

• From the Gauss's law we can write,

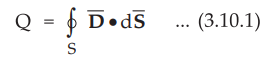
• While the charge enclosed in a v

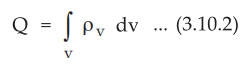
• But according to Gauss's law in the point form,

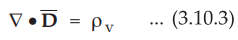
Using in equation (3.10.2),

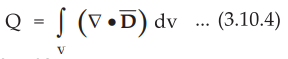
Equating equations V3.10.1) and (3.10.4),

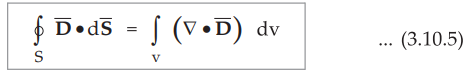
• The equation (3.10.5) is called divergence theorem. It is also called the Gauss-Ostrogradsky theorem. The theorem can be stated as,

• The integral of the normal component of any vector field over a closed surface is equal to the integral of the divergence of this vector field throughout the volume enclosed by that closed surface.

• The theorem can be applied to any vector field but partial derivatives of that vector field must exist. The equation (3.10.5) is the divergence theorem as applied to the flux density. Both sides of the divergence theorem give the net charge enclosed by the closed surface i.e. net flux crossing the closed surface.

• With the help of the divergence theorem, the surface integral can be converted into a volume integral, provided that the closed surface encloses certain volume. Thus volume integral on right hand side of the theorem must be calculated over a volume which must be enclosed by the closed surface on left hand side. The theorem is applicable only under this condition.

Points to remember while solving problems.

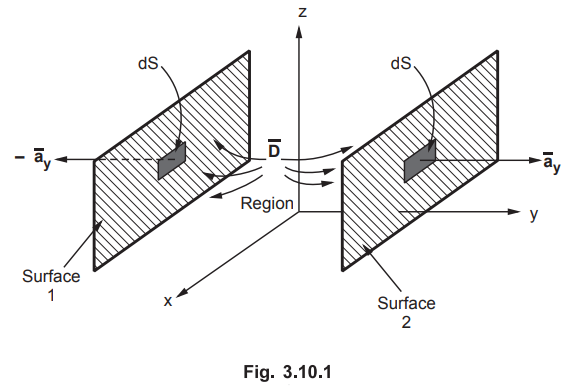
1. Draw the sketch of the surface enclosed by the given conditions.

2.  acts within the region bounded by given conditions towards the various surfaces. Thus note the direction of surface with respect to region in which  is given to give proper sign to the unit vector while defining . For example, consider the region bounded by two planes as shown in the Fig. 3.10.1. For surface 1, with respect to  in the region, dS is in  direction. While for surface 2, with respect to  in the region, dS is in  direction.

3. Then evaluate 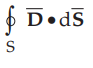 over all the possible surfaces.

4. Evaluate 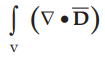 dv to verify the divergence theorem. Take care of variables in the partial derivatives.

1. Proof of Divergence Theorem

• According to divergence theorem, the surface integral is converted into a volume integral, provided that the closed surface encloses certain volume. Let the closed surface encloses certain volume v. Subdivide this volume v into a large number of subsections called cells. Let the vector field associated with the surface S is . Then if Ith cell has the volume Av_i and is bounded by the surface S_i then we can write,

• The cells are adjacent to each other hence the outward flux to one cell is inward to its neighbouring cells. Thus on every interior surface between the cells, there is cancellation of surface integrals and hence the sum of the surface intergrals over surfaces S_i s is equal to the total surface

integral over the entire surface S.

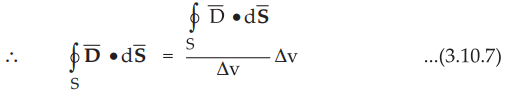
• Taking Lim Av tends to zero of right hand side i.e. as the volume shrinks about a point, the right hand side of the equation (3.10.7) gives divergence of , according to the definition of the divergence.

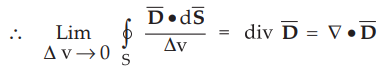
• Using in the equation (3.10.7),

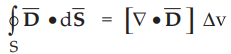
• For considering entire volume, integrate right hand side over the entire volume v, enclosed by the surface S.

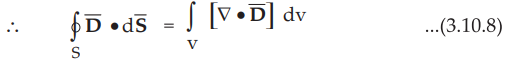
• The equation (3.10.8) is the statement of the divergence theorem and hence divergence theorem is proved. The theorem is very effective as the evaluation of volume integral is easier than to evaluate the surface integral.

Ex. 3.10.1 Given 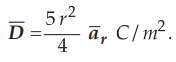. Evaluate both the sides of divergence theorem for the volume enclosed by r = 4 m and θ = π / 4.

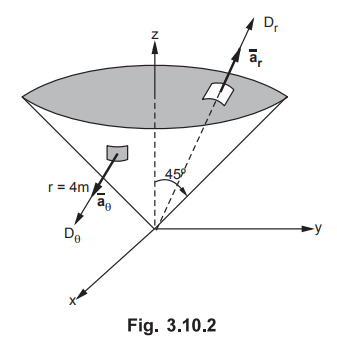
Sol. : The given  is in spherical co-ordinates. The volume enclosed is shown in the Fig. 3.10.2.

According to divergence theorem,

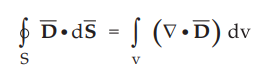
The given  has only radial component as given.

Ex. 3.10.2 Given that 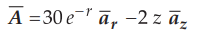 in the cylindrical co-ordinates. Evaluate both sides of the divergence theorem for the volume enclosed by r = 2, z = 0 and z = 5.

Sol. : The divergence theorem states that

Ex. 3.10.3 If G(r) =  dtmin the flux of G(r) out of entire suface f the cylinder r = 1, 0 ≤ z ≤ 1.

Sol. :  The cylinder is shown in the Fig. 3.10.4.

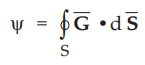
There are three surfaces = 0S₁, S₂ and S₃ i.e. top, curved and bottom.

Examples for Practice

Ex. 3.10.4 In region r ≤ ɑ in spherical co-ordinates,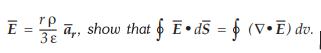 

Review Question

1. State and prove Divergence theorem.