DLC Solved Semester Question Paper 2017 May (2013 Reg)

Solved Paper

Sem – III [EEE] Regulation 2013

MAY - 2017

Digital Logic Circuits

 

Time : 3 Hours]   [Total Marks : 100

PART - A (10 × 2 = 20 Marks)

 

Q.1 Reduce a(b + bc) + ab'.   

Ans. 

 

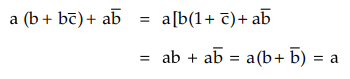
Q. 2 Convert 143₁₀ into its Unary and Unary coded decimal equivalent.

Ans.                              

 

Q.3 Write the POS form of the SOP expression f (x, y,z) = x 'yz + xyz + xy 'z.

Ans. :

 

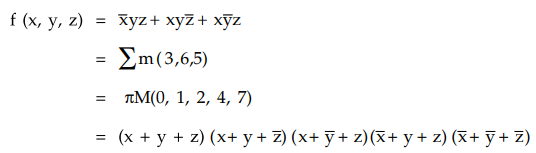
Q.4 Design a Half Subtractor.

(Refer section 3.12.1)

Q.5 Give the characteristic equation and characteristic table of a T Flip Flop.

(Refer section 4.6)

Q.6 State the differences between Moore and Melay state machines.

(Refer section 5.2.3)

Q.7 What is a flow table ? Give example.

(Refer section 7.6.1)

Q.8 State the difference between PROM, PAL and PLA.

(Refer section 9.5)

Q.9 Give the syntax for package declaration and package body in VHDL.

(Refer sections 10.2.4 and 10.2.5)

Q.10 Write the VHDL code for 2x1 multiplexer using behavioral modeling.

(Refer example 10.7.3)

 

PART - B (5 × 13 = 65 Marks)

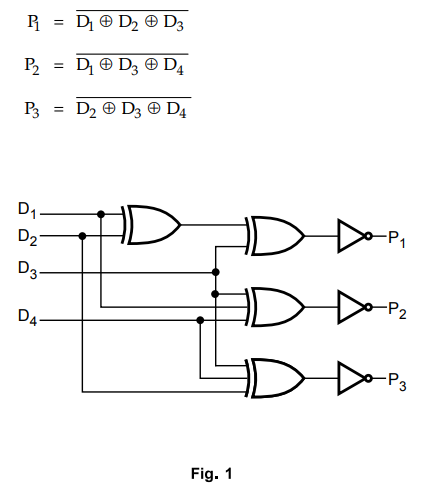
Q.11 a) i) Design a odd - parity hamming code generator and detector for 4 - bit data and explain their logic.

Ans. :

For P₁ : D₁, D₂ and D₃ bits are considered

For P₂ : D₁, D₃ and D₄ bits are considered

For P₃ : D₂, D₃ and D₄ bits are considered

Ex - OR logic gives logic 1 output for odd number ones in the inputs.

We need to set priority bit = 0 if there are odd number of ones in the input

Therefore, for odd parity

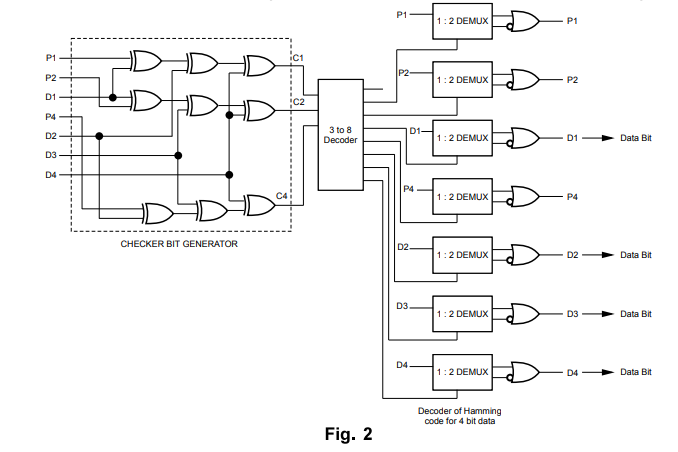
In the decoder circuit, code word is applied as input. Then check bits are generated by the checker bit generator to check the parity bits. These check bits locates the error in the code word by means of decoder circuit. The output of decoder enables a demultiplexer which are connected to the input code words. If no error occurs then the select line of demultiplexer flows the input form line 10 and the II is set to logic T'. So from the logic OR gate we can obtain the data. Now if an error occur then the select line of the demultiplexer flows the code word from line II and 10 is set to logic 'O'. Thus inverting the bits, the error bit is corrected and thus we can obtain the error free data. A decoder circuit of hamming code for 4 bit data word is also shown in Fig. 2

 

ii) Convert FACE₁₆ into its binary, octal and decimal equivalent.

Ans . :

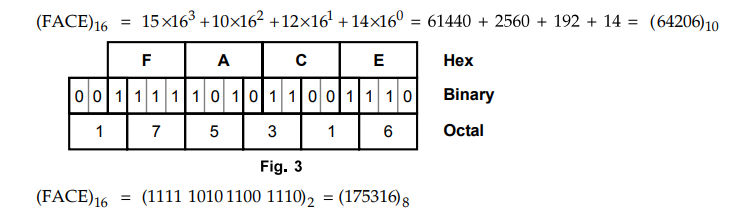
OR

b) i) With circuit schematic explain the working of a two - input TTL NAND gate.

(Refer section 2.5.2)

ii) Compare totem pole and open collector outputs.

(Refer section 2.5.6)

 

Q.12 a) i) Reduce the following minterms using Karnaugh – Map

f (w, x, y, z) = ∑ m (0,1,3,5,6,7,8,12,14) + ∑ d (9,15)

Ans.

 

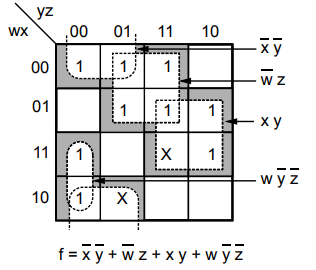
ii) Implement the following function using a suitable multiplexer

f (a,b,c) = ∑ m(3,7,4,5) (Refer similar example 3.17.7)

OR

b) i) Design a 3 × 8 decoder and explain its operation as a minterm generator.

(Refer example 3.19.1)

ii) Design a full adder using only NOR gates.

Ans. : Refer Table 3.11.2 and Fig. 3.11.6.

We have,

 

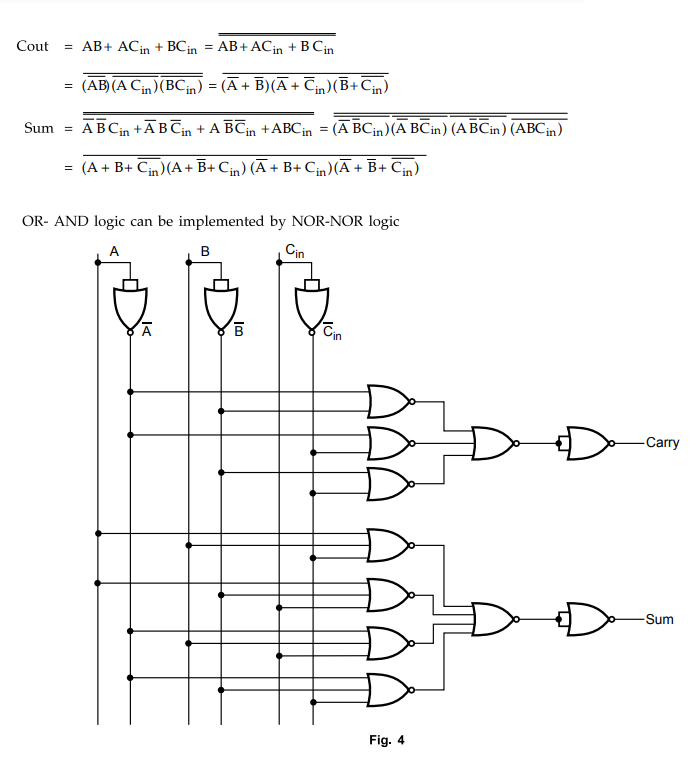
Q.13 a) i) Draw and explain the operation of a Master - Slave JK Flip Flop.

(Refer section 4.5)

ii) Design a 5 - bit ring counter and mention its applications.

(Refer section 6.6)

OR 

b) i) Design a 4 - bit parallel - in serial - out shift register using D Flip Flops.

(Refer section 6.3.3) [7]

ii) Using partitioning minimization procedure reduce the following state table :

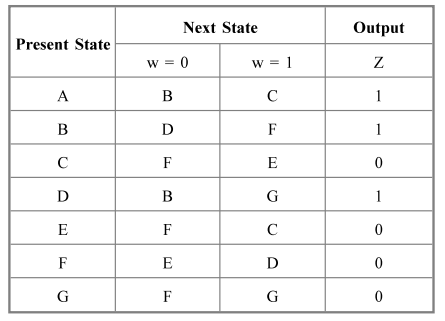
Ans. : Refer section 5.4.1.2 for procedure

Step 1 : 1 – equivalent

P₁ = (A, B, D)(C, E, F, G)

Step 2 : 2 – equivalent

P₂ = (A, B, D)(C, E, G) (F)

Step 3 : 3 – equivalent

P₃ = (A, D)(B)(C, E, G)(F)

The states in the common blocks of P₃ are equivalent and redundant. Therefore, states A = D and C = E = G.

Minimized state table :

 

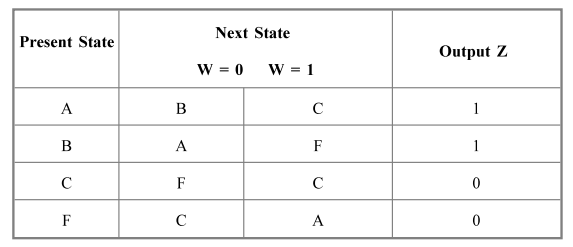
Q.14 a) A control mechanism for a vending machine accepts nickels and dimes. It despense merchandise when 20 cents is deposited; it does not give change if 25 cents is deposited. Design the FSM that implements the required control, using as few states as possible. Find a suitable assignment and derive next - state and output expressions.    [13]

Ans. : Coins are deposited one at a time. The coin-sensing mechanism generates signals N = 1 and D = 1 when it sees a nickel or a dime, respectively. It is impossible to have N = D = 1 at the same time. Following the insertion of a coin for which the sum equals or exceeds 20 cents, the machine releases the merchandise and resets to the initial state.

Fig. 5 shows a state diagram for the required FSM. It is derived using a straight forward approach in which all possible sequences of depositing nickels and dimes are enumerated in a treelike structure. To keep the diagram uncluttered, the labels D and N denote the input conditions DN = 10 and DN = 01, respectively. The condition 

DN = 00 is labeled simply as 0. The merchandise is released in states F, H, and K, which are reached after 20 cents has been deposited, and in states I and L, upon a deposit of 25 cents.

The corresponding flow table is given in Figure 2. It can be reduced using the partitioning procedure as follows

P1 = (ADGJ)(BE)(C)(FIL)(HK)

P2 = (A)(D)(GJ)(B)(E)(C)(FIL)(HK)

P₃ = P₂

Using G to represent the equivalent states G and J , F to represent F, I , and L, and H to represent H and K yields a partially reduced flow table in Fig. 7. The merger diagram for this table is presented in Figure 4. It indicates that states C and E can be merged, as well as F and H. Thus the reduced flow table is obtained as shown in Fig. 9(a). The same information is depicted in the form of a state diagram in Fig. 10.

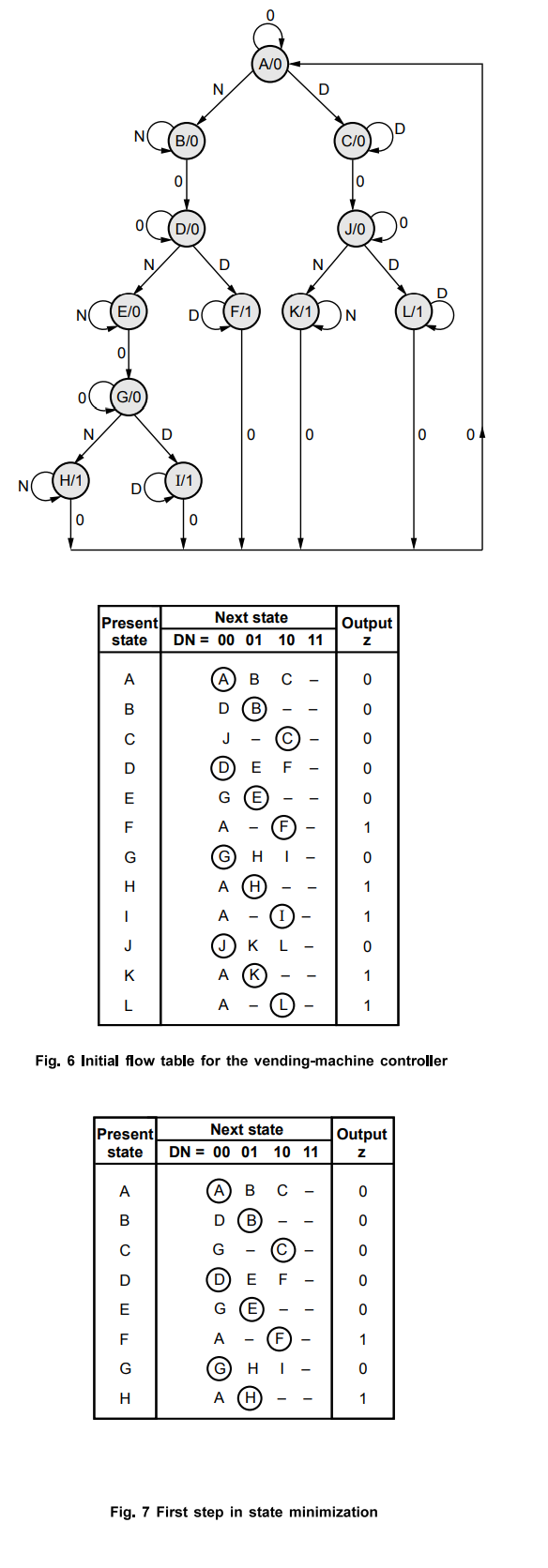
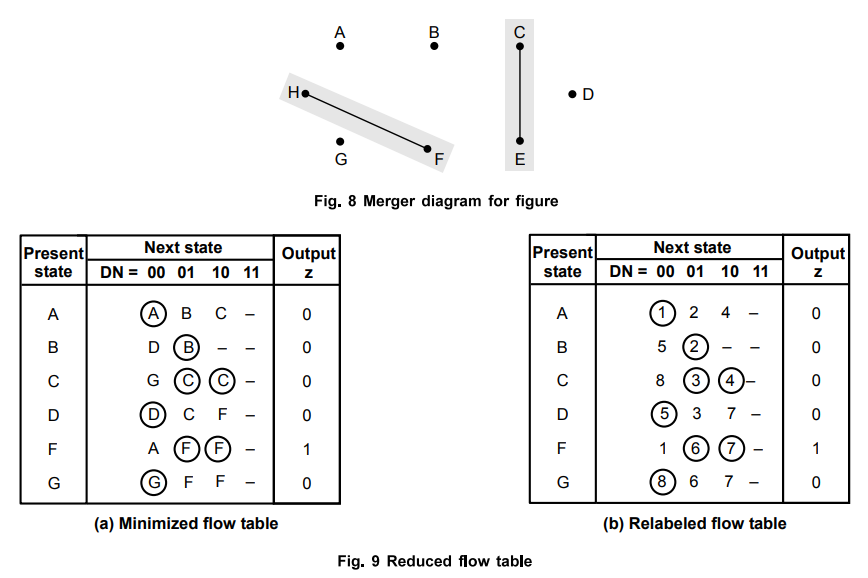
Next a suitable state assignment must be found. The flow table is relabeled in Fig. 9(b) to associate a unique number with each stable state. Then the transition diagram in Fig. 11(a) is obtained. Since we wish to try to embed the diagram onto a three dimensional cube, eight vertices are shown in the figure. The diagram shows two diagonal transitions. The transition between D and G (label 7) does not matter, because it is only an alternative path. The transition from A to C (label 4) is required, and it can be realized via unused states as indicated in Fig. 11(b). Therefore, the transition diagram can be embedded onto a three-dimensional cube as shown. Using the state assignment from this figure, the excitation table in Fig. 12 is derived.

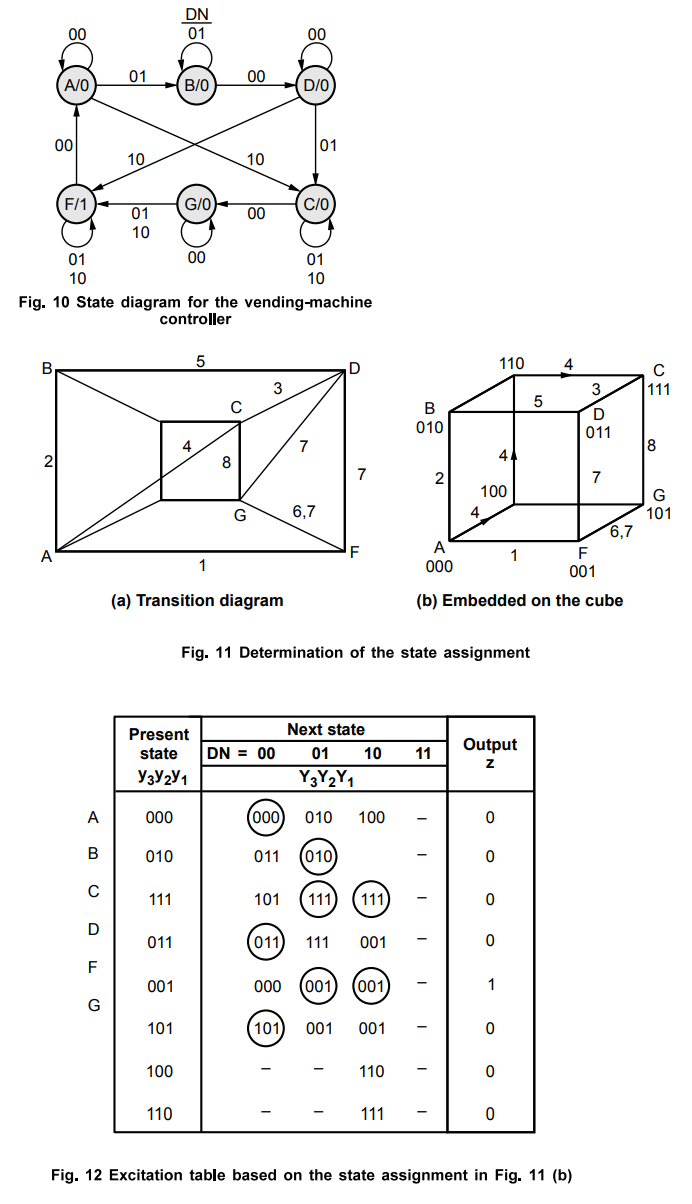
OR

b) i) Implement the following logic and analyse for the pressure of any hazard 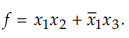. If hazard is present briefly explain the type of hazard and design a hazard - free circuit. (Refer section 8.1.1)     [7]

ii) Implement the following functions using programmable logic array :

f1 ( x, y, z) = ∑ m(1,3,5,7)

f2(x,y,z) = ∑ m(2,4,6) (Refer similar example 9.3.3)

 

Q.15 a) Design a 3 - bit magnitude comparator and write the VHDL code to realize it using structural modeling.

(Refer listing 10.9.8) [13]

b) Design a 4 × 4 array multiplier and write the VHDL code to realize it using structural modeling. [13]

Ans. : VHDL Code for 4×4 Array Multiplier

entity Array_Mult is

port (X. Y : in bit_vector (3 downto 0);

P : out bit_vector (7 downto 0);

end Anray_Mult;

architecture Behavioral of Array_Mult is

signal Cl, C2, C3; bitvector (3 downto 0);

signal SI, S2, S3; bit_vector (3 downto 0);

signal XY1, XY2, XY3; bit_vector (3 downto 0);

component FullAdder

port (X, Y, Cin : in bit;

Cout, Sum : out bit);

end component;

component HalfAdder

port (X, Y : in bit;

Cout, Sum : out bit);

end component; 

begin

XYO(O) ← X(0) and Y(0); XY1(O) ←  X(0) and Y(l);

XYO(l) ←  X(l) and Y(0); XY1(1) ← X(1) and Y(l);

XY0(2) ← X(2) and Y(0); XY1(2) ← X(2) and Y(l);

XY0(3) ←  X(3) and Y(0); XY1(3) ← X(3) and Y(l);

 

XY2(0) ←  X(0) and Y(2); XY3(0) ← X(0) and Y(3);

XY2(1) ←  X(l) and Y(2); XY3(1) ← X(1) and Y(3);

XY2(2) ← X(2) and Y(2); XY3(2) ← X(2) and Y(3);

XY2(3) ← X(3) and Y(2); XY3(3) ← X(3) and Y(3);

 

FA1 : FullAdder port map (XY0(2), XY1(1), Cl(0), Cl(l), Sl(l));

FA2 : FullAdder port map (XY0(3), XY1(2), Cl(l), Cl(2), Sl(2));

FA3 : FullAdder port map (Sl(2), XY2(1), C2(0), C2(l), S2(l));

FA4 : FullAdder port map (Sl(3), XY2(2), C2(l), C2(2), S2(2));

FA5 : FullAdder port map (Cl(3), XY2(3), C2(2), C2(3), S2(3));

FA6 : FullAdder port map (S2(2), XY3(1), C3(0), C3(l), S3(l));

FA7 : FullAdder port map (S2(3), XY3(2), C3(l), C3(2), S3(2));

FA8 : FullAdder port map (C2(3), XY3(3), C3(2), C3(3), S3(3));

HA1 : HalfAdder port map (XYO(l), XY1(O), C1(O), Sl(0));

HA2 : HalfAdder port map (XY1(3), Cl(2), Cl(3), Sl(3));

HA3 : HalfAdder port map (Sl(l), XY2(0), C2(0), S2{0));

HA4 : HalfAdder port map (S2(l), XY3(0), C3(0), S3(0));

P(0) ← XY0(0); P(l) ← Sl(0); P(2) ← S2(0);

P(3) ← S3(0); P(4) ← S3(l); P(5) ← S3(2);

P(6) ← S3(3); P(7) ← C3(3);

end Behavioral;

 

PART C (1 × 15 = 15 Marks)

 

Q. 16 a) Design a CMOS inverter and explain its operation. Comment on its characteristics such as Fan - in, Fan - out power dissipation, propagation delay and noise margin. Compare its advantages over other logic families.

(Refer sections 2.6.3, 2.2 and 2.6.7) [15]

OR

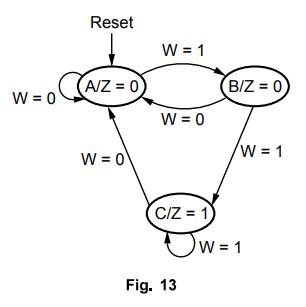
b) Write the VHDL code for the given state diagram, using behavioral modeling. Design it using one - hot state assignment and implement it using Programmable Array Logic (PAL). [15]

Ans. : VHDL code for given state diagram

LIBRARY IEEE:

USE IEEE.std_logic_1164.all;

ENTITY SEQ IS,

PORT (Clock, Reset, W : IN STDLOGIC;

Z : OUT_STD LOGIC);

End SEQ;

ARCHITECTURE Behaviour of SEQ IS,

TYPE state_type IS (A, B, C);

SIGNALY : state_type;

BEGIN

IF Reset = '0' THEN

Y = A;

ELSEIF (clock1 EVENT AND CLOCK = T') THEN

CASE Y IS

WHEN A ⇒

if W = '0' THEN

Y< = A;

ELSE

Y < = B;

END IF;

WHEN B ⇒

IF W = '0' THEN

Y < A;

ELSE

Y < = C;

END IF;

WHEN C ⇒

IFW '0'THEN

Y < = A;

ELSE

Y < = C;

END IF;

END CASE;

END IF;

END PROCESS;

Z < = '1' WHEN Y = C ELSE '0';

END BEHAVIOR

State table for the given sequential circuit is shown in table 1

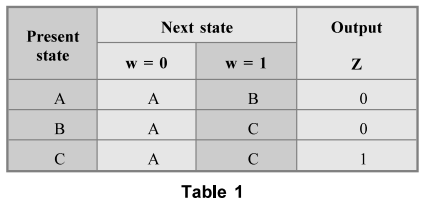
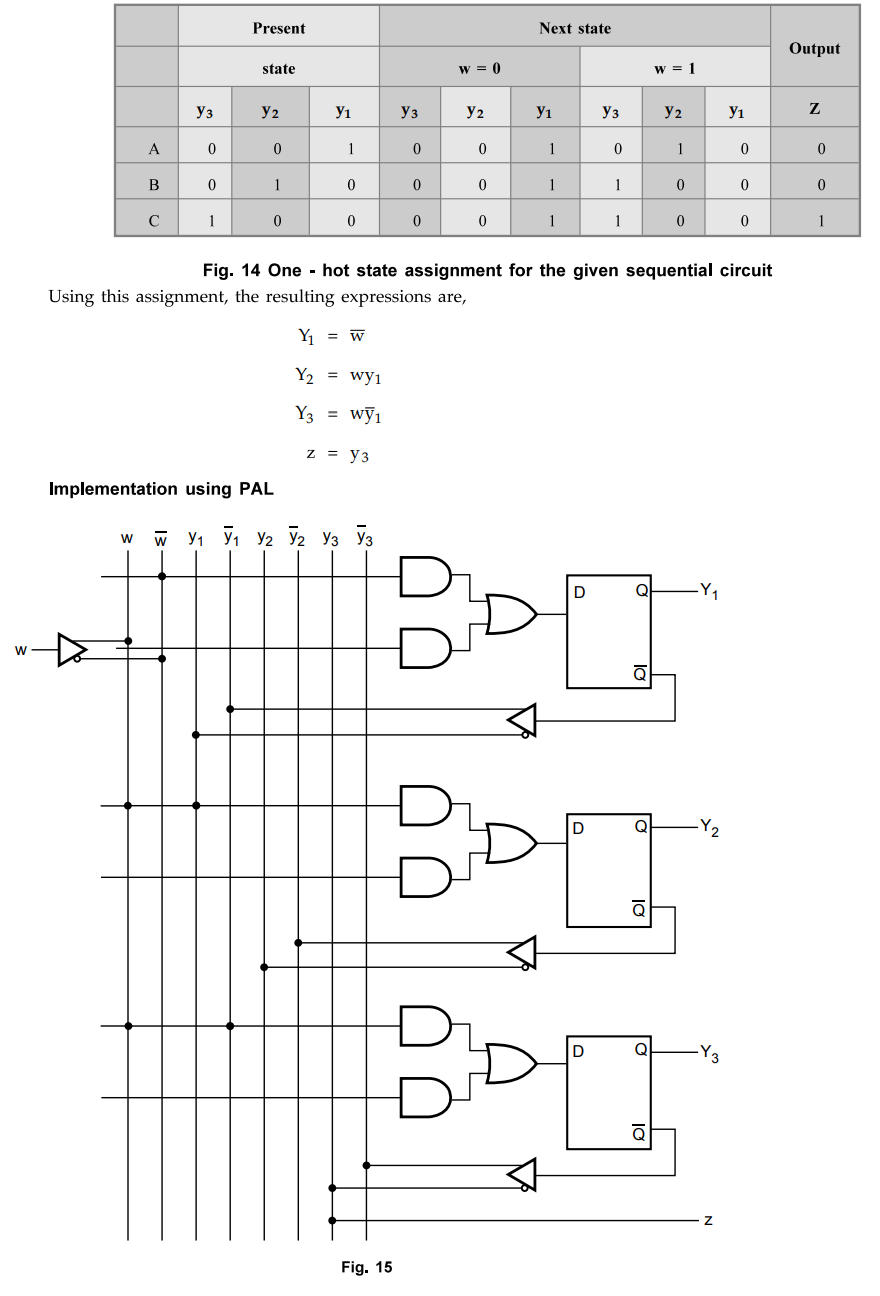
Fig. 14 shows how one-hot state assignment can be applied to the given sequential circuit. Because there are three states, it is necessary to use three state variables. The chosen assignment is to represent the states A, B, and C using the valuations y3 y2 yi = 001, 010, and 100, respectively. The remaining five valuations of the state variables are not used. They can be treated as don't cares in the derivation of the next-state and output expressions.