Double Revolving Field Theory

Double Revolving Field Theory AU : May-12, 13, 17, Dec.-05, 12, 15, 16, 17

According to this theory, any alternating quantity can be resolved into two rotating components which rotate in opposite directions and each having magnitude as half of the maximum magnitude of the alternating quantity.

In case of single phase induction motors, the stator winding produces an alternating magnetic field having maximum magnitude of ϕ_lm.

According to double revolving field theory, consider the two components of the stator flux, each having magnitude half of maximum magnitude of stator flux i.e. (ϕ1m / 2). Both these components are rotating in opposite directions at the synchronous speed N_s which is dependent on frequency and stator poles.

Let ϕ_f is forward component rotating in anticlockwise direction while ϕ_h the backward component rotating in clockwise direction. The resultant of these two components at any instant gives the instantaneous value of the stator flux at that instant. So resultant of these two is the original stator flux.

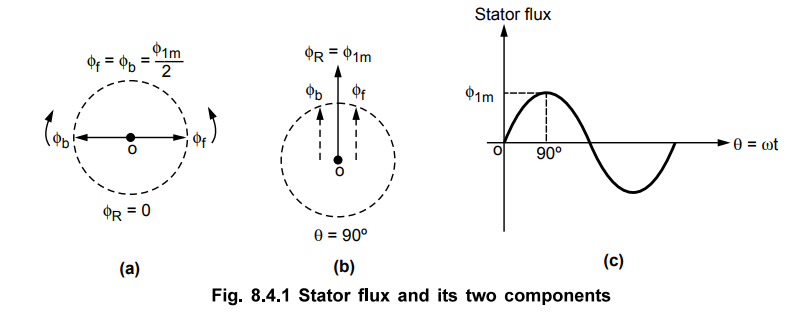
The Fig. 8.4.1 shows the stator flux and its two components ϕ_f and ϕ_h. At start both the components are shown opposite to each other in the Fig. 8.4.1 (a). Thus the resultant R = 0. This is nothing but the instantaneous value of stator flux at start. After 90°, as shown in the Fig. 8.4.1 (b), the two components are rotated in such a way that both are pointing in the same direction. Hence the resultant ϕ_E is the algebraic sum of the magnitudes of the two components. So ϕ_R = ϕ_1m /2) + (ϕ_1m /2) = ϕ_1m. This is nothing but the instantaneous value of the stator flux at 0 = 90° as shown in the Fig. 8.4.1 (c). Thus continuous rotation of the two components gives the original alternating stator flux.

Both the components are rotating and hence get cut by the rotor conductors. Due to cutting of flux, e.m.f. gets induced in rotor which circulates rotor current. The rotor current produces rotor flux. This flux interacts with forward component f to produce a torque in one particular direction say anticlockwise direction. While rotor flux interacts with backward component ϕ_b to produce a torque in the clockwise direction. So if anticlockwise torque is positive then clockwise torque is negative. 

At start these two torques are equal in magnitude but opposite in direction. Each torque tries to rotate the rotor in its own direction. Thus net torque experienced by the rotor is zero at start. And hence the single phase induction motors are not self starting.

1. Torque-Speed Characteristics

The two oppositely directed torques and the resultant torque can be shown effectively with the help of torque-speed characteristics. It is shown in the Fig. 8.4.2.

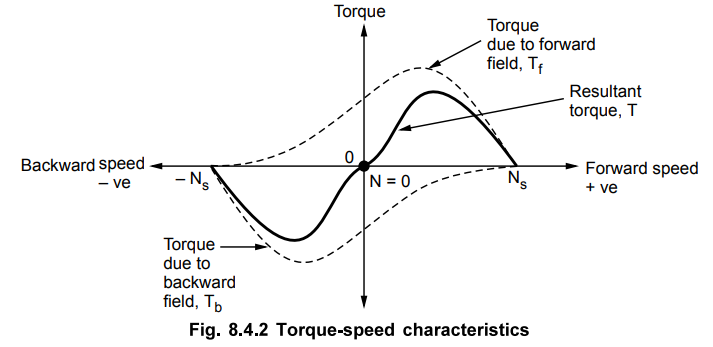
It can be seen that at start N = 0 and at that point resultant torque is zero. So single phase motors are not self starting.

However if the rotor is given an initial rotation in any direction, the resultant average torque increases in the direction in which rotor is initially rotated. And motor starts rotating in that direction. But in practice it is not possible to give initial torque to rotor externally hence some modifications are done in the construction of single phase induction motors to make them self starting.

Another theory which can also be used to explain why single phase induction motor is not self starting is cross-field theory. 

Review Questions

1. Explain the double revolving field theory as applied to single phase induction motor and show that single phase induction motor is not self starting. AU : May-12, 13, 14, 17 Dec.-12, 15, 16, 17 Marks 8

2. Show that a single phase sinusoidal field can be replaced by two fields rotating around the air gap in opposite directions; sketch the slip torque curve due to each field. Prove that the motor has no starting torque.