E.M.F. Equation of a Transformer

E.M.F. Equation of a Transformer

AU May-04,05,07,12,14,15, Nov.-07, Dec.-12,17

• When the primary winding is excited by an alternating voltage V₁, it circulates alternating current, producing an alternating flux ϕ.

• The primary winding has N₁ number of turns. The alternating flux o linking with the primary winding itself induces an e.m.f. in it denoted as E₁.

• The flux links with secondary winding through the common magnetic core. It produces induced e.m.f. E₂ in the secondary winding. This is mutually induced e.m.f.

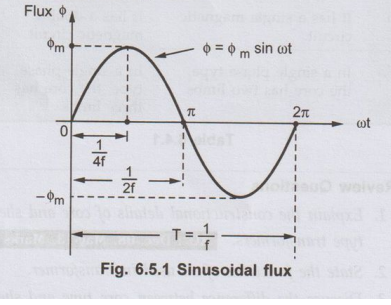
• The primary winding is excited by purely sinusoidal alternating voltage. Hence the flux produced is also sinusoidal in nature having maximum value of ϕ_m as shown in the Fig. 6.5.1.

The various quantities which affect the magnitude of the induced e.m.f. are:

Φ = Flux and

ϕ_m = Maximum value of flux

N₁ = Number of primary winding turns

f = Number of secondary winding turns

E₁ = Frequency of the supply voltage

E₂ = R.M.S. value of the primary induced e.m.f.

• From Faraday's law of electromagnetic induction the average e.m.f. induced in each turn is proportional to the average rate of change of flux.

Average e.m.f. per turn

• Consider the ¼^th cycle of the flux as shown in the Fig. 6.5.1. Complete cycle gets completed in 1/f seconds. In ¼ ^th time period, the change in flux is from 0 to ϕ_m

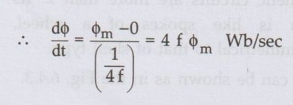
as dt for ¼ ^th time period is ¼ f seconds

 Average e.m.f. per turn = 4 f ϕ_m

• As ϕ is sinusoidal, the induced e.m.f. in each turn of both the windings is also sinusoidal in nature.

For sinusoidal quantity,

Form Factor = R.M.S. value / Average value = 1.11

R.M.S. S. value = 1.11 × Average value

R.M.S. value of induced e.m.f. per turn

= 1.11 x 4 f ϕ_m = 4.44 f ϕ_m

• There are N₁ number of primary turns hence the R.M.S. value of induced e.m.f. of primary denoted as E₁ is,

E₁ = N₁ x 4.44 f ϕ_m volts

• While as there are N₂ number of secondary turns the R.M.S. value of induced e.m.f. of secondary denoted E₂ is,

E₂ = N₂ × 4.44 f ϕ_m volts

• The expressions of E₁ and E₂ are called e.m.f. equations of a transformer.

E₁ = 4.44 f ϕ_m N₁ volts...(6.5.1)

E₂ = 4.44 f ϕ_m N₂ volts.....(6.5.2)

 

1. Concept of Ideal Transformer

• A transformer is said to be ideal if it satisfies following properties :

i) It has no losses.

ii) Its windings have zero resistance.

iii) Leakage flux is zero i.e. 100 % flux produced by primary links with the secondary.

iv) Permeability of core is so high that negligible current is required to establish the flux in it.

 

2. Ratios of a Transformer

• Consider a transformer shown in Fig. 6.5.2 indicating various voltages and currents.

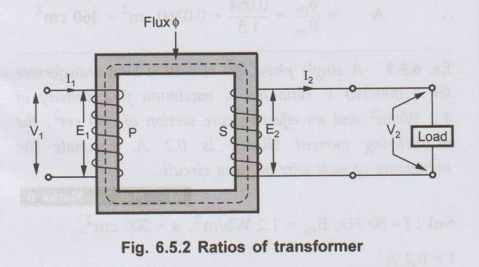
1. Voltage ratio: We know from the e.m.f. equations,

E₁ = 4.44 f ϕ_m N₁ and

E₂ = 4.44 f ϕ_m N₂

Taking ratio of the two equations we get,

E₂ /  E_1c = N₂ / N₁ =  K

This ratio of secondary induced e.m.f. to primary induced e.m.f. is known as voltage transformation ratio denoted as K.

Thus, E₂ = K E₁ where K = N₂/ N₁.

1. If N₂ > N₁ i.e. K > 1, we get E₂ > E₁ then the transformer is called step-up transformer.

2. If N₂ < N₁ i.e. K < 1, we get E₂ < E₁, then the transformer is called step-down transformer.

3. If N₂ = N₁ i.e. K = 1, we get E₂ = E₁ then the transformer is called isolation transformer or 1:1 transformer.

2. Current ratio : For an ideal transformer there are no losses. Hence the product of primary voltage V₁ and primary current I₁, is same as the product of secondary voltage V₂ and the secondary current 1₂.

Hence the currents are in the inverse ratio of the voltage transformation ratio.

 

3. Volt-Ampere Rating

• When electrical power is transferred from primary winding to secondary there are few power losses in between. These power losses appear in the form of heat which increase the temperature of the device.

• This temperature must be maintained below certain limiting value as it is always harmful from insulation point of view.

• The copper loss (I²R) in the transformer depends on the current 'I' through the winding while the iron or core loss depends on the voltage 'V' as frequency of operation is constant.

• None of these losses depend on the power factor (cos ϕ) of the load. Hence losses decide the temperature rise and hence the rating of the transformer.

• As losses depend on V and I only, the rating of the transformer is specified as a product of these two parameters V×L Hence the transformer rating is specified as the product of voltage and current are called VA rating.

• On both sides, primary and secondary VA rating remains same. This rating is generally expressed in kVA (kilo volt amperes rating).

kVA rating of a transformer =V₁ I₁ / 1000 = V₂ I₂ / 1000 ........ 1000 to express in KVA

 

4. Full Load Currents

• If V₁ and V₂ are the terminal voltages of primary and secondary then from specified kVA rating we can decide full load currents of primary and secondary, I₁ and I₂.

•This is the safe maximum current limit which may carry, keeping temperature rise below its limiting value.

•  These values indicate, how much maximum load can be connected to a given transformer of a specified kVA rating.

The full load primary and secondary currents indicate the safe maximum values of currents which transformer windings can carry.

Ex. 6.5.1 A 100 kVA, 3300 V/240 V, 50 Hz, Single phase transformer has 990 turns on the primary. Calculate the number of turns on secondary and the approximate value of primary and secondary full load currents. AU May-15, Marks 10

Sol. :

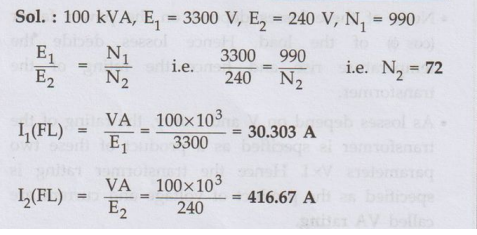
Ex. 6.5.2 The e.m.f. per turn of a single-phase, 6.6 kV, 440 V, 50 Hz transformer is approximately 12 V. Calculate number of turns is the HV and LV windings and the net cross-sectional area of the core for a maximum flux density of 1.5 T.

Sol. :

Ex. 6.5.3 A single phase, 50 Hz, 1000 kVA transformer the for 12000/240 V ratio has a maximum flux density of 1.2 Wb/m² and an effective core section of 300 cm², magnetising current (RMS) is 0.2 A. Estimate the inductance of each wire on open circuit.  AU May-12, Marks 6

Sol. :

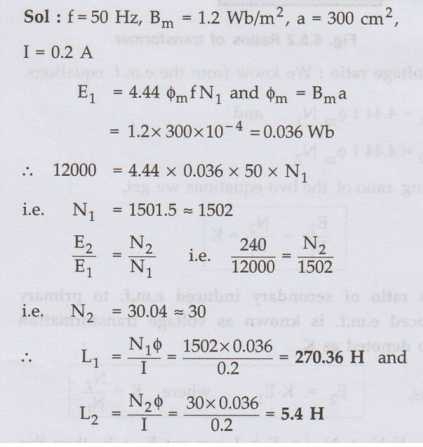
Ex. 6.5.4  The voltage per turn of a single phase transformer is 1.1 volt, when the primary winding is connected to a 220 volt, 50 Hz AC supply the secondary voltage is found to be 550 volt. Find the primary and secondary turns and core area if maximum flux density is 1.1 Telsa. AU Dec.-12, Marks 8

Sol. :

Refer example 6.5.2 for the procedure and verify the answers as, N₁ = 200, N₂ = 500,A= 45.04 cm²

Review Questions

1. Develop an equation for induced e.m.f. in a transformer winding in terms of flux and frequency. AU May-04, 05, 12, 14, Dec.-12,17, Marks 8

2. State the relationships between voltages and currents on primary side and secondary side of a single phase transformer.

3. Explain the various features of an ideal transformer.

4. What is kVA rating of a transformer?

5. A single phase transformer has 480 turns on primary and 90 turns on the secondary. The mean length of flux path in the core is 1.8 m and joints are equivalent to an air gap of 1 mm. The maximum value of the flux density is to be 1.1 T when a potential difference of 2200 volts at 50 Hz is applied to the primary. Assume value of magnetic field strength corresponding to the flux density of 1.1 T in the core to be 400 A/m. Calculate

i) The cross-section area of the core ii) Maximum value of the magnetizing current

iii) Secondary voltage on no load.

[Ans. : i) 0.01876 m² ii) 1.500 A iii) 412.5 volts]

 6. A single-phase, 50 Hz transformer has 80 turns on the primary winding and 400 turns on the secondary winding. The net cross-sectional area of the core is 200 cm². If the primary winding is connected to a 240 V, 50 Hz supply, determine: i) The e.m.f. induced in the secondary winding. ii) The maximum value of the flux density in the core. [Ans.: E₂ = 1200 V, B_m = 0.6756 Wb/m²]

7. A single phase transformer has 350 primary and 1050 secondary turns. The primary is connected to 400 V, 50 Hz a.c. supply. If the net cross sectional area of the core is 50 cm², calculate i) The maximum value of the flux density in the core ii) The induced e.m.f. in the secondary winding. [Ans. : B_m = 1.0296 Wb/m², E₂ = 1200 V]

8. A single phase transformer has 500 turns on its primary and 1000 turns on secondary.

The voltage per turn in the primary winding is 0.2 volts. Calculate,

i) Voltage induced in the primary winding

ii) Voltage induced in the secondary winding

iii) The maximum value of the flux density if the cross section area of the core is 200 cm²

iv) kVA rating of the transformer if the current in primary at full load is 10 A, the frequency is 50 Hz.

[Ans.: i) E₁ = 100 volts, ii) E₂ = 200 volts,iii)ϕ_m= 9.009 × 10-⁴ Wb iv) B_m= 0.045 web/m² or Tesla ]

9. For a single phase transformer having primary and secondary turns of 440 and 880 respectively, determine the transformer kVA rating if half load secondary current is 7.5 A and maximum value of on core flux is 2.25 mWb. [Ans.: 6.5934 KVA]