Effect of Atmospheric Conditions on Transmission Line

Effect of Atmospheric Conditions on Transmission Line

The expressions derived uptil now are true in still air and the normal temperature. In these derivations we have assumed that the conductor is acted by its weight only.

But the performance of the transmission line gets affected by the atmospheric conditions in the areas through which it is running. If it is running through the area where winter is severe and the area experiences a snowfall then there is ice coating on the transmission line. Such coating increases the weight. Similarly in hilly areas, the transmission line gets subjected to tremendous force of wind. Such widely varying conditions must be considered while designing the transmission line, in calculating sag and the tension in the line conductor.

Let us, study the effect of two severe atmospheric conditions on sag and the tension calculations.

These conditions are,

1. Ice coating and 2. Wind pressure

 

1. Effect of Ice Coating

When the transmission line is coated with ice, the thickness and size of the conductor increases. This thickness depends on the weather conditions. This causes increase in weight of the conductor. Increase in weight increases the vertical sag. The weight of ice acts vertically downwards, in the same direction as that of the conductor.

Consider a conductor with diameter 'd'. It is coated with ice of thickness't' as shown in the Fig. 4.4.1. Hence the overall diameter of the coated conductor is D.

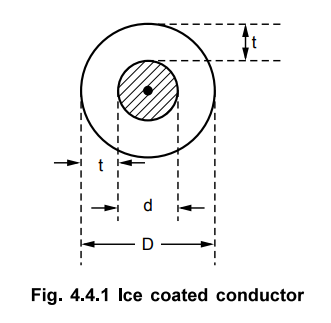
It can be seen that,

D = d + 2t

and the area of the coated conductor is

= π / 4 D²

Hence the area of the ice covering,

Ai = π / 4 [D² – d²]

If D and d are in metres then this area A; represents the area in m² i.e volume of ice in m³ per metre length of the conductor. Knowing that density of ice is 915 kg/m³ , the total weight of ice can be obtained as,

2. Effect of Wind Pressure

The wind flows horizontally and hence the wind pressure on the conductor is considered to be acting perpendicular to the conductor. Thus force due to wind acts at right angles to the projected surface of the conductor as shown in the Fig. 4.4.2.

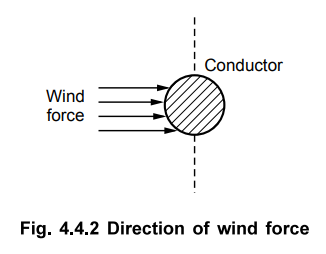
The wind force w_w can be obtained as,

w_w = Wind force per unit length in kg/m

= Wind pressure per unit area × Projected surface area per unit length

= Wind pressure × [(d + 2t) × 1]

W_w = P [(d + 2t)]

where            p = Wind pressure in kg/m² , d - Diameter of conductor

t = Thickness of ice coating if exists

Hence the conductor gets acted upon by two additional forces, the one vertically downwards w_i and one in horizontal direction w_w. 

 

3. Effect of Ice and Wind

Let W = Weight of conductor itself acting vertically down

W_i = Weight of ice acting vertically down

w_w = Wind force acting horizontally

Hence the total force acting on the conductor is vector sum of the horizontal and vertical forces as shown in the Fig. 4.4.3.

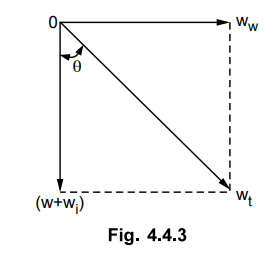
Thus,

Hence it is necessary to note the following points :

1. The sag direction is at an angle 0 measured with respect to vertical. Hence the sag is called slant sag. This is calculated by the expression derived earlier, considering the total weight w_t.

Slant sag S = wt L² / ST

2. The conductor adjusts itself in a plane which is at an angle 0 with respect to vertical. The angle is given by,

tan θ = W_w / (W + W_i)

3. As slant sag S is the direction at an angle θ with respect to vertical, the vertical sag is cosine component of the slant sag S.

Vertical sag = S cos θ

 

Example 4.4.1 An overhead transmission line has a span of 230 m and the conductor weight is 650 kg/km. Calculate the maximum sag if the breaking stress is 4465 kg/cm2 while the area of the conductor is 1.29 cm2. Assume factor of safety as 2.

Solution :

L = Span = 230 m

 

Example 4.4.2 An overhead transmission line has a span of 200 m, between the supports. The supports are at the same level. The area of cross-section of conductor is 1.9 cm while the ultimate strength is 5000 kg/cm . The specific gravity of the conductor material is 8.9gm/cm . If the conductor is subjected to the wind pressure of 1.5 kg/m length, calculate the sag if factor of safety is 5. Also calculate the vertical sag.

Solution :   L = 200 m and A = 1.9 cm²

Ultimate strength = 5000 kg/cm² = 5000 × 1.9 kg = 9500 kg

Vertical sag = S cos θ = 5.9484 × cos (41.574) = 4.45 m 

 

Example 4.4.3 An overhead transmission line has a span of 200 m and is supported by towers at the equal level. The weight of the conductor is 125 kg per 100 m length of wire. The ultimate stress for the conductor is 4500 kg/cm² . If the sag of the line is 3.6 m, calculate the factor of safety. The line is subjected to the wind pressure of 100 kg/m² . The area of cross-section of conductor is 1.25 cm² .

Solution :

 

Example 4.4.4 A transmission line has a span of 250 m is supported by towers at the same level. The area of the conductor 1.29 cm². The breaking stress for the conductor is 4220 kg/cm . Assume factor of safety as 3. The wind pressure is 45 kg/m² . Find the height of the conductor above ground level at which it should be supported if minimum clearance of 7 m is to be kept between ground and conductor. Assume density of conductor material as 8.9 gm/cm³ .

Solution :  

Vertical sag = S cos θ = 5.5311 × cos (26.67) = 4.9427 m

The minimum clearance required is 7 m and vertical sag is 4.9427 m.

Hence the height of conductor above ground level at which it should be supported is,

= 7 + 4.9427 = 11.9427 m

 

Example 4.4.5 A transmission line conductor has an effective diameter of 91.5 mm and weighs 0.85 kg/m. If the maximum permissible sag with the horizontal wind pressure of 39 kg/m² of projected area and 12.7 mm radial ice coating is 6.3 m, calculate the permissible span between the two supports at the same level allowing a factor of safety as 2. The ultimate strength of the conductor is 8000 kg and density of ice is 910 kg/m3. Solution d = 91.5 mm, w = 0.85 kg/m³, S 2, strength 8000 kg, S 6.3 m³

Solution :

 

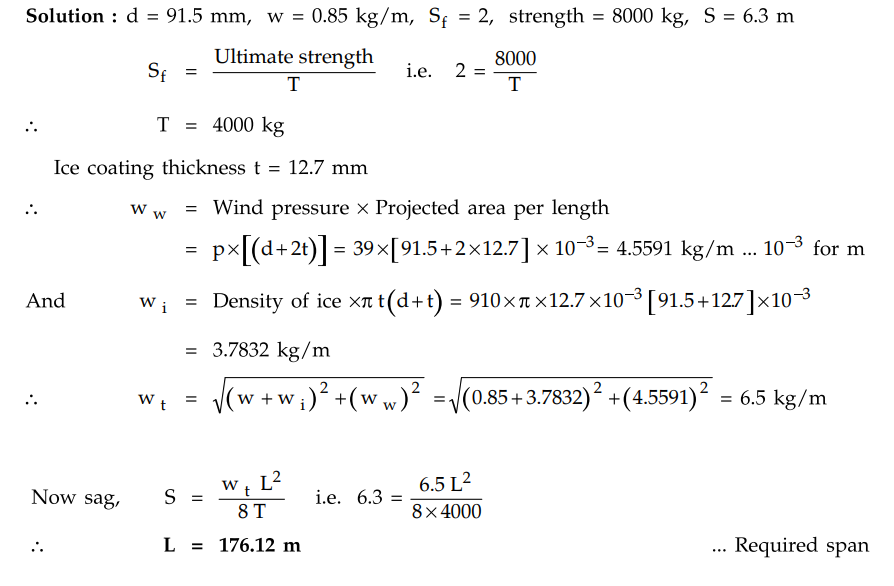
Example 4.4.6 A transmission line conductor is supported on the towers of unequal heights. The first tower has a height of 30 m and the second tower has a height of 50 m. The distance between the towers is 150 m. Tension in the conductor is 2200 kg and cross section of the conductor is 2 cm2. The specific gravity of the conductor material is 9.5 gm / cm³ and the wind pressure is 150 kg / m². Calculate the sag.

Solution : The towers and the sags are shown in the Fig. 4.4.6.

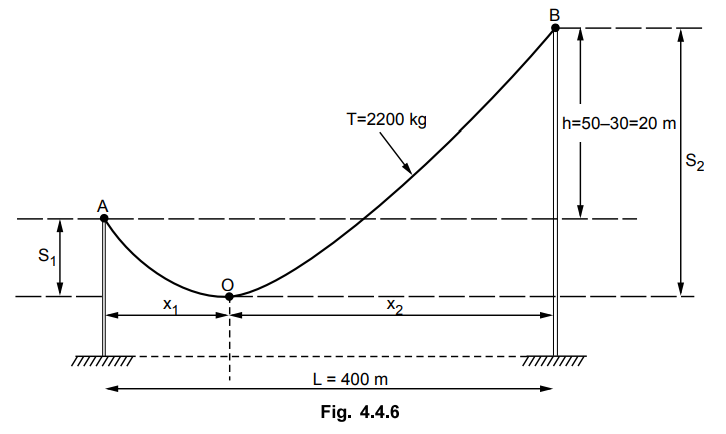
The height of tower A is 30 m and that of B is 50 m hence,

Note that x₁ is negative which indicates that the lowest point of the trajectory i.e. point O occurs to the left of the support A. This clears the fact that the lowest point of trajectory does not exist between the supports A and B. This is shown in the Fig. 4.4.7.

 

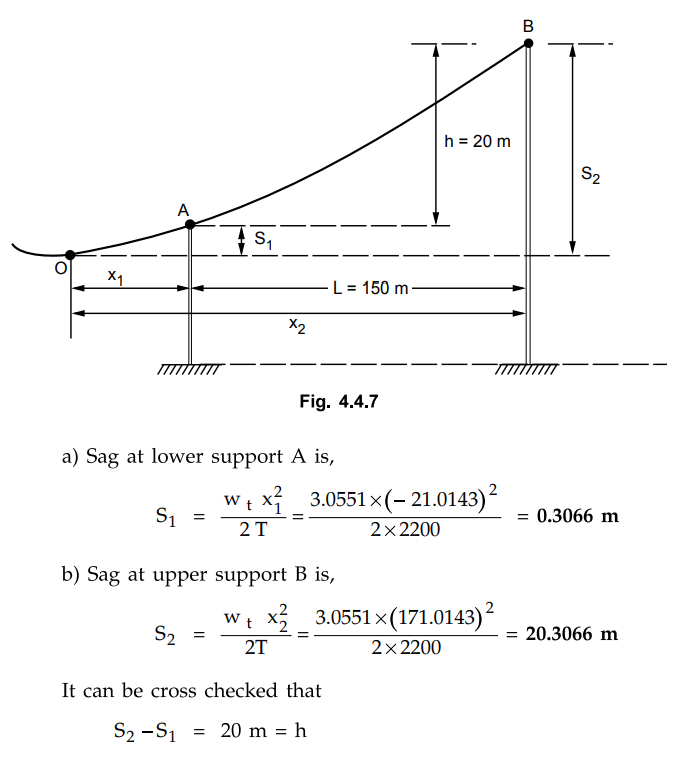
Example 4.4.7 An overhead line has a span of 150 m between level supports. The conductor has a cross-sectional area of 2 cm² . The ultimate strength is 5000 kg/cm and safety factor is 5. The specific gravity of the material is 8.9 gm/cc. The wind pressure is 1.5 kg/m. Calculate the height of the conductor above the ground level at which it should be supported if a minimum clearance of 7 m is to be left between the ground the conductor.

Solution :   L = 150 m, a = 2 cm², Sf = 5, ww = 1.5 kg/m , density = 8.99 m/cm³ 

 

Example 4.4.8 A transmission line conductor having a dia of 19.5 mm weights 0.85 kg/m. The span is 275 meters. The wind pressure is 39 kg/m² of projected area with ice coating of 13 mm. The ultimate strength of the conductor is 8000 kg. Calculate the maximum sag if the factor of safety is 2 and ice weighs 910 kg/m³

AU : Dec -07, 14, May-16,18, Marks 13

Solution :

Review Questions

1. What are the factors influencing sag ?

2. Derive an expression for the sag of a transmission line when the supports are at equal levels taking into the effect of wind and ice loading.

3. A transmission line has a span of 225 m and weighs 75 kg per 100 m. The line conductor has a cross-sectional area of 3.1 cm and has an ultimate breaking strength of 1250 kg/cm . Assuming that the line is covered with ice and provides a load of 1 kg/m while the wind pressure provides a load of 1.4 kg/m, calculate the maximum sag produced. Take safety factor of 3. Also determine the vertical sag.       

[Ans.: 10.98 m, 8.574 m]

4. A transmission line has a span of 275 metres, between level supports. The conductor has an effective diameter of 1.96 cm and weighs 0.865 kg/cm. Its ultimate strength is 8060 kg. If the ice has a coating of radical thickness of 1.27 cm and is subjected to a wind pressure of 3.9 g/cm projected area. Calculate the sag for a safety factor of 2. Weight of lcc of ice is 0.91 g. 

[Ans.: 4030 kg,6.3 m]

5. An overhead transmission line uses copper of nominal area of 110 mm . It uses stranded conductor of size 37/2.79 mm. It weighs 844 kg per 1000 m. The breaking strength of the material is 7950 kg. The factor of safety is 2. The wind pressure is 75 kg/m of projected area. The line is supported by the towers with a span of 300 m. Calculate the maximum sag in the conductor.

[Ans.: 4.78 m]