Electromagnetic Theory: Unit I: (b) Coulombs Law and Electric Field Intensity
Electric Field due to Infinite Line Charge
Solved Example Problems
• Consider an infinitely long straight line carrying uniform line charge having density ρL C/m. Let this line lies along z-axis from -∞ to ∞ and hence called infinite line charge.
Electric Field due to
Infinite Line Charge
AU : Hay-06, 07, 12, 15, 16, 17,
18, Dec.-03, 06, 08, 09, 14
•
Consider an infinitely long straight line carrying uniform line charge having
density ρL C/m. Let this line lies along z-axis from -∞ to ∞ and
hence called infinite line charge.
Let point P is on y-axis at which electric field intensity is to be determined.
The distance of point P from the origin is 'r' as shown in the Fig. 2.6.1.

•
Consider a small differential length dZ carrying a charge dQ, along the line as
shown in the Fig. 2.6.1. It is along z-axis hence dZ = dz.
dQ
= ρL dl = ρL dz ...
(2.6.1)
•
The co-ordinates of dQ are (0, 0, z) while the co-ordinates of point P are (0,
r, 0). Hence the distance vector ![]() can be written as,
can be written as,

Note :
For every charge on positive z-axis there is equal charge present on negative
z-axis. Hence the z component of electric field intensities produced by such
charges at point P will cancel each other. Hence effectively there will not be
any z component of ![]() at P. This is shown in the Fig. 2.6.2.
at P. This is shown in the Fig. 2.6.2.

Note : For
such an integration, use the substitution
z
= r tan θ i.e. r = z/tan θ
dz
= r sec2 θ dθ
•
Here r is not the variable of integration.
For z = -∞ , θ = tan-1 (-∞) = - π/2
= -90o
For
z = +∞, θ = tan-1 (∞) = π/ 2 = + 90°
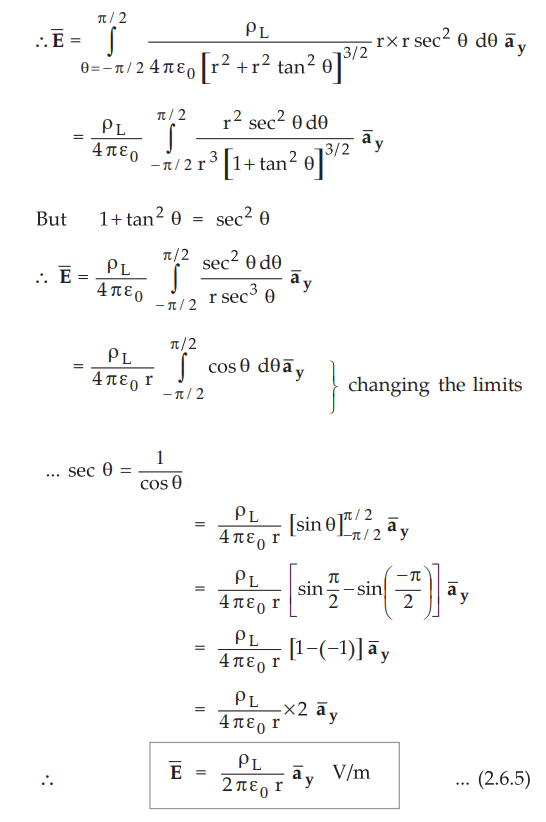
Key Point :
If without considering symmetry of charges and without cancelling z component
from d ![]() , if integration is carried out, it gives the same answer. The
integration results the z component of
, if integration is carried out, it gives the same answer. The
integration results the z component of ![]() to be mathematically zero.
to be mathematically zero.
•
The result of equation (2.6.5) which is specifically in cartesian system can be
generalized. The ![]() is unit vector along the distance r which is
perpendicular distance of point P from the line charge. Thus in general
is unit vector along the distance r which is
perpendicular distance of point P from the line charge. Thus in general 
•
Hence the result of ![]() can be expressed as,
can be expressed as,
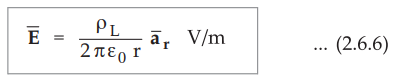
where r = Perpendicular distance of point P
from the line charge
![]() = Unit vector in the direction of the perpendicular distance of point P from
the line charge
= Unit vector in the direction of the perpendicular distance of point P from
the line charge
Very important notes : 1. The field
intensity ![]() at any point has no component in the direction parallel to the
line along which the charge is located and the charge is infinite.
For example if line charge is parallel to z-axis,
at any point has no component in the direction parallel to the
line along which the charge is located and the charge is infinite.
For example if line charge is parallel to z-axis, ![]() can not have
can not have ![]() component, if line charge is parallel to y-axis,
component, if line charge is parallel to y-axis, ![]() cannot have
cannot have ![]() component. This makes the integration calculations easy.
component. This makes the integration calculations easy.
2. The
above equation consists r and ![]() which do not have meanings of
cylindrical co-ordinate system. The distance r is to be obtained by distance
formula while
which do not have meanings of
cylindrical co-ordinate system. The distance r is to be obtained by distance
formula while ![]() is unit vector in the direction of
is unit vector in the direction of ![]() .
.
Key Point :
This result can be used as a standard result for solving other problems.
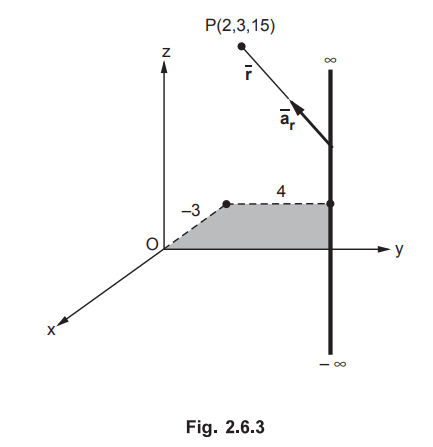
Ex. 2.6.1
A uniform line charge ρL = 25
nClm lies on the line x = -3 m and y = 4m in free space. Find the electric
field intensity at a point (2, 3, 15) m. AU : May-06, Marks 8
Sol. :
The line is shown in the Fig. 2.6.3. The line with x = - 3 constant and y = 4
constant is a line parallel to z axis as z can take any value. The ![]() at
P (2, 3, 15) is to be calculated.
at
P (2, 3, 15) is to be calculated.
The
charge is infinite line charge hence ![]() can be obtained by standard result,
can be obtained by standard result,
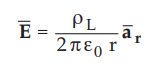
To
find ![]() , consider two points, one on the line which is (-3, 4, z) while P
(2, 3, 15). But as line is parallel to z
axis,
, consider two points, one on the line which is (-3, 4, z) while P
(2, 3, 15). But as line is parallel to z
axis, ![]() cannot have component in
cannot have component in![]() direction hence z need not be
considered while calculating
direction hence z need not be
considered while calculating ![]() .
.

Ex. 2.6.2 An infinitely long uniform line
charge is located at y = 3, z = 5. If ρL =30 nC/m, find the field
intensity ![]() at i) Origin ii) P(0, 6, 1) iii) P(5, 6, 1).AU: Dec.-08, Marks 8
at i) Origin ii) P(0, 6, 1) iii) P(5, 6, 1).AU: Dec.-08, Marks 8
Sol. : The
charge is shown in the Fig. 2.6.4.

The
charge is parallel to x-axis hence ![]() cannot have any component in x
direction hence do not consider x while calculating
cannot have any component in x
direction hence do not consider x while calculating ![]()

As ![]() does not have any component in x direction and y, z, co-ordinates are
same as in (ii) hence
does not have any component in x direction and y, z, co-ordinates are
same as in (ii) hence ![]() also remains same as obtained in (ii).
also remains same as obtained in (ii).
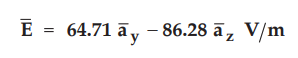
Ex. 2.6.3
Obtain an expression for electric field
intensity due to a uniformly charged line of length 'l'.AU : May-15, Marks 8
Sol. :
The charge of length l is shown in the Fig. 2.6.5 along x-axis.
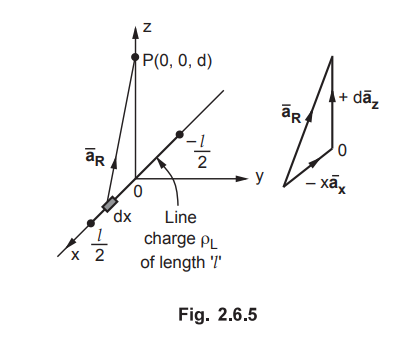
Let us obtain expression for ![]() at P(0,
0, d) located on z-axis. Consider differential length dZ = dx along the charge.
at P(0,
0, d) located on z-axis. Consider differential length dZ = dx along the charge.
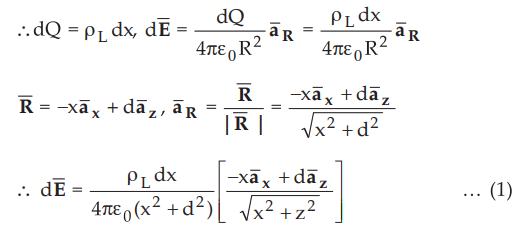
As
charge is symmetrical along x axis, there can not be x component of ![]() Hence ax part in equation (1), need not be considered.
Hence ax part in equation (1), need not be considered.
Examples for practices
Ex. 2.6.4 A uniform line charge, infinite in
extent with ρL = 20 nC/m lies along the z-axis. Find the ![]() at
(6, 8, 3) m.
at
(6, 8, 3) m.

Ex. 2.6.5 Two identical uniform line charges, with ρL = 75 nC/m are located in free space at x = 0, y = ± 0.4 m. What force per unit length does each line charge exert on the other ?
[Ans.: 0.7899 µN]
Ex. 2.6.6
A line charge density ρLis uniformly distributed over a length of 2a
with centre as origin along x-axis. Find ![]() at a point P which is on the
z-axis at a distance d.
at a point P which is on the
z-axis at a distance d.
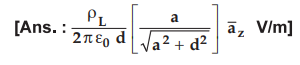
Ex. 2.6.7 Two uniform line charges of density ρl = 4 nC/m lie in the x = 0 plane at y = ± 4 m. Find E at (4, 0, 10) m.

Review Question
1. Derive an
expression for electric field intensity ![]() due to an uniformly charged
infinitely long straight line with constant charge density in C/m.
due to an uniformly charged
infinitely long straight line with constant charge density in C/m.
AU : May-07, Marks 10, Dec.-03, 06, 09, 14, Marks 16, 17,18, Marks 8
Electromagnetic Theory: Unit I: (b) Coulombs Law and Electric Field Intensity : Tag: : Solved Example Problems - Electric Field due to Infinite Line Charge
Related Topics
Related Subjects
Electromagnetic Theory
EE3301 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
