Electromagnetic Theory: Unit I: (b) Coulombs Law and Electric Field Intensity
Electric Field due to Infinite Sheet of Charge
Solved Example Problems
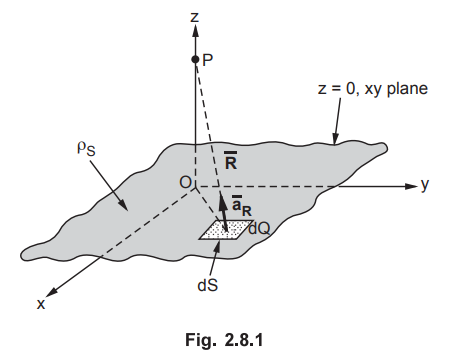
• Consider an infinite sheet of charge having uniform charge density ρ5 C/m2, placed in xy plane as shown in the Fig. 2.8.1. Let us use cylindrical coordinates.
Electric
Field due to Infinite Sheet of Charge
AU : May-03, 06, 07, 09, 10,
Dec.-03,04, 06, 07, 09, 10, 16 June-09
•
Consider an infinite sheet of charge having uniform charge density ρ5
C/m2, placed in xy plane as shown in the Fig. 2.8.1. Let us use
cylindrical coordinates.
•
The point P at which ![]() to be calculated is on z-axis.
to be calculated is on z-axis.
•
Consider the differential surface area dS carrying a charge dQ. The normal
direction to dS is z direction hence dS normal to z direction is r dr dϕ.
Now
dQ = ρS dS = p S r dr dϕ ...
(2.8.1)
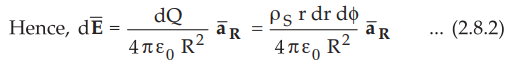
•
The distance vector ![]() has two components as shown in the Fig. 2.8.2.
has two components as shown in the Fig. 2.8.2.

•
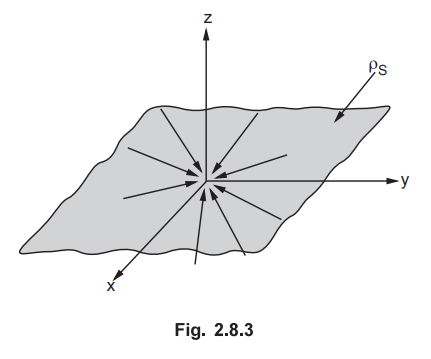
For infinite sheet in xy plane, r varies from 0 to while varies from 0 to 2π.
Note : As
there is symmetry about z-axis from all radial direction, all ![]() components
of
components
of ![]() are going to cancel each other and net
are going to cancel each other and net ![]() will not have any radial
component.
will not have any radial
component.
•
Hence while integrating d![]() there is no need to consider
there is no need to consider ![]() component.
Though if considered, after integration procedure, it will get mathematically
cancelled.
component.
Though if considered, after integration procedure, it will get mathematically
cancelled.
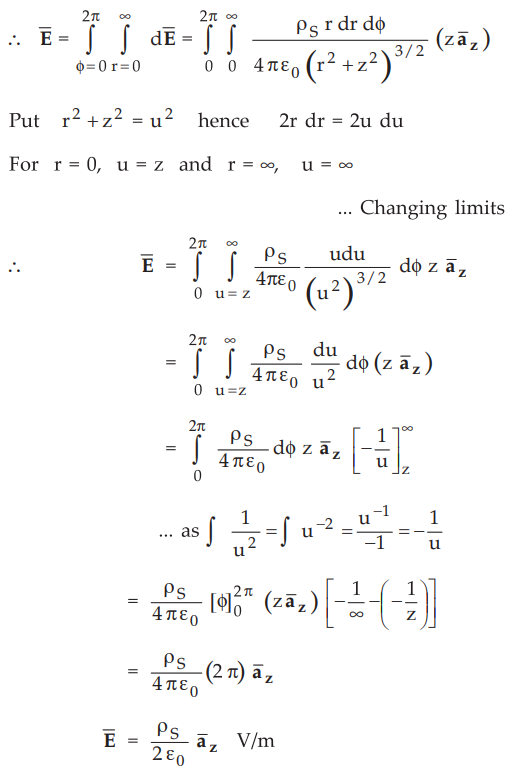
...
For points above xy plane
•
Now ![]() is direction normal to differential surface area dS considered.
Hence in general if
is direction normal to differential surface area dS considered.
Hence in general if ![]() is direction normal to the surface containing
charge, the above result can be generalized as,
is direction normal to the surface containing
charge, the above result can be generalized as,

...
For points below xy plane.
Note :
The equation (2.8.6) is standard result and can be used directly to solve the
problems.
Key Point :
Thus electric field due to infinite sheet of charge is everywhere normal to the
surface and its magnitude is independent of the distance of a point from the
plane containing the sheet of charge.
Important observations :
1. ![]() due to infinite sheet of charge at a point is not dependent on the
distance of that point from the plane containing the charge.
due to infinite sheet of charge at a point is not dependent on the
distance of that point from the plane containing the charge.
2.
The direction of ![]() is perpendicular to the infinite charge plane.
is perpendicular to the infinite charge plane.
3.
The magnitude of ![]() is constant every where and given by
is constant every where and given by 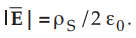
Ex. 2.8.1 Find the force on a point charge q
located at (0,0, h) m due to charge of surface charge density ρs C/m2
uniformly distributed over the circular disc r ρ ≤ a, z = 0 m Also find
electric field intensity at the same point.AU
: May-03, 06, 07, 09, 10, Dec.-03, 04, 07, 09, 10, 16, Marks 10
Sol. :
The charges are shown in the Fig. 2.8.4.
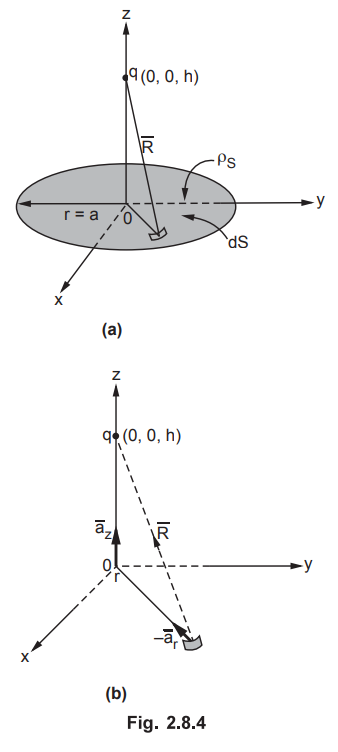
Consider
the differential area dS carrying the charge dQ. The normal direction to dS is ![]() hence
hence
dSz
= r dr dϕ
dQ
= ρS dS = ρS r dr dϕ
Thus
the force on a point charge q due to dQ is,
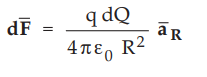
The ![]() can be splitted as shown in the Fig. 2.8.4 (b),
can be splitted as shown in the Fig. 2.8.4 (b),

Key Point :
Due to symmetry about z-axis, all radial components will cancel each other.
Hence there will not be any component of 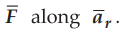 So in the
integration
So in the
integration ![]() need not be considered.
need not be considered.

Ex. 2.8.2
A sheet of charge lies in yz plane at x =
0 and has uniform surface charge density of 5.0 pC/m2. Find the electric field
at a point P (- 5, 0, 0) on x-axis. AU:
Dec.-06, June-09, Marks 10
Sol. :
The sheet is shown in the Fig. 2.8.5.
The
point P is on the back side of the plane.
The
Normal to the plane in the direction of P is 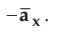
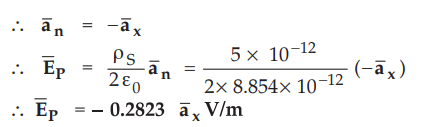
Ex. 2.8.3
An infinite sheet with surface charge Q =
12 ε0 Cm-2 is lying in the plane x - 2y + 3z = 4. Find an
expression for the field-intensity on the side of the plane containing the
origin.
Sol. :
The plane is shown in the Fig. 2.8.6. The plane can be defined uniquely from
three points which can be obtained from the equation of plane x-2y + 3z = 4.
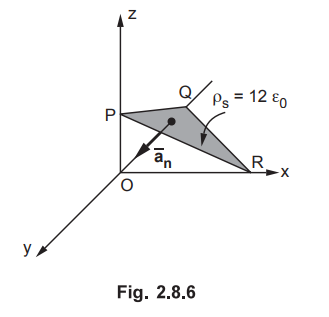
For
x = 0 , y = 0 , z = 4/3 P(0,0,4/3)
For
x = 0, z = 0, y = -2 Q(0.-2,0)
For
y = 0, z = 0, x = 4 (4,0,0)
The
three poionts P, Q and R define a plane.
The plane is infinite sheet of charge.
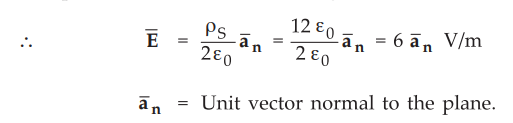
Note :
If plane is defined as Ax + By + Cz = D then the unit vector normal to the
plane is,
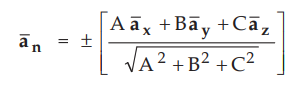
Positive
sign for front side of the plane and negative sign for back side of the plane.
In
this case, A = 1, B = - 2, C = 3, D = 4
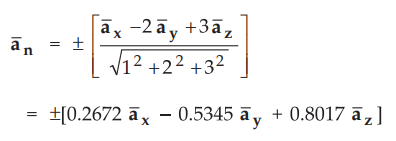
The
origin is on the back side of the plane so use negative sign.
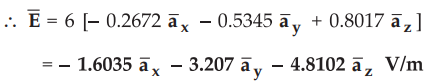
Examples
for Practices
Ex.
2.8.4 Charge lies in y = - 5 m plane in the
form of an infinite square sheet with a uniform charge density of ps = 20
nC/m2. Determine ![]() at all the points.
at all the points.
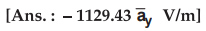
Ex.
2.8.5 Determine the force on a point charge
of 5 nC at (0, 0, 5) m due to uniformly distributed charge of 5 mC over a
circular disc of radius r ≤ lm in z = 0
plane.
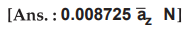
Ex.
2.8.6 Find ![]() at P (1, 5, 2) m in
free space if a point charge of 6 uC is located at (0,0, 1), the uniform line
charge density
at P (1, 5, 2) m in
free space if a point charge of 6 uC is located at (0,0, 1), the uniform line
charge density
PL
= 180 nC/m along × axis and uniform
sheet of charge with ps = 25 nC/m2 over the plane z = -1.
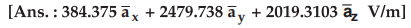
Ex.
2.8.7 The charge lies on the circular disc r ≤
4 m, z = 0, with density ps = [l0-4/r]
c/m2.
Determine ![]() at r = 0, z = 3 m.
at r = 0, z = 3 m.
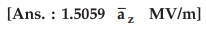
Ex.
2.8.8 A sheet of charge lies in yz plane at x
= 0 and has uniform surface charge density of 5.0 pC/m2. Find the electric
field at a point P (- 5, 0, 0) on x-axis.
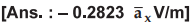
Ex.
2.8.9 A circular disc of 10 cm radius is
charged uniformly with a total charge. Find ![]() at a point 20 cm on its axis.
at a point 20 cm on its axis.
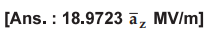
Ex.
2.8.10 A charge distribution is placed in the
z = -3 m plane in the form of a square sheet defined by -2 ≤ x ≤
2m, -2 ≤ y ≤ 2m. It has a charge density of ps = 2(x2 + y2
+ 9)3/2 nC/m2. Find the electric field intensity
(![]() ) at the origin.
) at the origin.
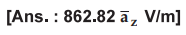
Ex.
2.8.11 Three infinite uniform sheets of charge
are located in free space follows 3 nC/m2 at z = - 4, 6 nC/m2
at z = 1 and - 8 nC/m2 at z = 4.
Find ![]() at the point :
at the point :
i)
PA = (2, 5, -5),
ii)
PB = (4, 2, -3),
iii)
PC = (-1, -5, 2),
iv)
PD = (-2, 4, 5).

Ex.
2.8.12 Find electric field intensity ( ![]() )
at origin if the following charge distributions are
present in the free space :
)
at origin if the following charge distributions are
present in the free space :
i)
Point charge 12 nC at P(2, 0, 6),
ii)
Uniform line charge density 3 nC/m at x = - 2, y =3.
iii)
Uniform surface charge density 0.2 nC/m2 at x = 2.
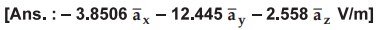
Review Questions
1. Find ![]() due to infinite sheet of charge placed in x-y plane and having
uniform surface charge density of ps C/m2 .
due to infinite sheet of charge placed in x-y plane and having
uniform surface charge density of ps C/m2 .
2. A circular disc of
radius 'a' m is charged uniformly with a charge density of ps C/m2.
Find the electric field at a point 'h' m from the disc along its axis.
Electromagnetic Theory: Unit I: (b) Coulombs Law and Electric Field Intensity : Tag: : Solved Example Problems - Electric Field due to Infinite Sheet of Charge
Related Topics
Related Subjects
Electromagnetic Theory
EE3301 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
