Electrical Power (p)

ELECTRICAL POWER (P)

The rate at which work is done in an electrical circuit is called electrical power and its unit is joule per second or watt. When one coulomb of electric charge is moved through a potential difference of one volt in one second, the rate of work is one joule per second or one watt. Hence, power in electric circuits is obtained as a product of the voltage (E or V) and the current (I).

P V.I Watts ……. (7)

We may write this as

P =I²R (or) P = V²/R …….  (8)

using Ohm's law.

Electrical Energy

Electrical energy is the total amount of work done and hence is the product of power and time.

W = Pt = V I t =I² Rt = (V²/R) t joules (Watt-second) ….(9)

Since the watt-second (joule) is a small unit for practical purposes, we use the kilowatt hour (kWh). This is sometimes called one Electrical unit. (or one Board of Trade unit or B.O.T unit)

1 kWh = 1 unit Power in watts × Time in seconds / 1000 × 60 × 60

EXAMPLE 4: What will be the current drawn by a lamp rated at 250 V, 40 Watts connected to a 230 V supply?

Solution

Rated power = 40 W

Rated voltage = 250 V

If R be the resistance of the filament, P = V²/R

40 =  (250)² / R

R =  (250)² / 40  = 1562.5 Ω

Current drawn from 230 V supply V/R =  230 / 1562.5 = 0.1472 A

EXAMPLE 5: An electric heater draws 8 A from 250 V supply. What is its power rating? Also find the resistance of the heater element.

Solution

Power rating = V. I = 8 × 250 = 2000 Watts

Resistance = V / I = 250 / 8 = 31.25 Ω

EXAMPLE 6: Twenty lamps each of 60 watts are used each for 4 hours per day in a building. Calculate (i) the current drawn when all the lamps are working and (ii) the monthly electricity charge at 55 paise per unit. Assume a supply of 240 V.

Solution

Current drawn by one lamp = P/V = 60 / 240 = 0.25 A

Total current drawn by 20 lamps = 20 × 0.25 = 5 A

Energy consumed in a month = 30 × 4 × 20 × 60 Wh

30 × 4 × 20 × 60 / 1000 = kWh = 144 units

Monthly Electric Charge = 144 × 0.55 Rs. 79.20

EXAMPLE 7: A resistor with a current of 3 A through it converts 500 J of electrical energy into heat energy in 12 second. What is the voltage across the resistor? (AU/CSE - June 2007)

Solution

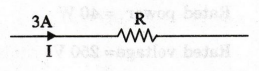
Energy = V I t

500 = V × 3 × 12

V = 500 / 3 × 12 = 13.88 V

V=18.88 V

EXAMPLE 8: A 5 Ω resistor has a voltage rating of 100 V, what is its power rating? (AU/CSE June 2007)

Solution

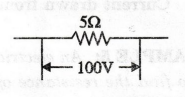
Power: V² / R = 100² / 5

P = 2000 W