Electromagnetic Wave Equations in Phasor Form

Electromagnetic Wave Equations in Phasor Form

AU: Dec.-07, 10, 13, May-10, 13

• An electromagnetic wave in a medium can be completely defined if intrinsic impedance (ɳ) and propagation constant (ɤ) of a medium is known. Thus it is necessary to derive the expressions for n and y interms of the properties of a medium such as permeability (µ) permittivity (Ɛ), conductivity (σ) etc.

• Consider Maxwell's equation derived from Faraday's law,

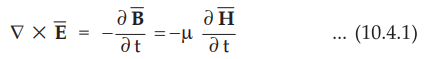
• Taking curl on both the sides of the equation,

• Consider a general electromagnetic wave with both the fields,  and   varying with respect to time. When any field varies with respect to time, its partial derivative taken with respect to time can be replaced by jω. Rewriting equation (10.4.5) in phasor form,

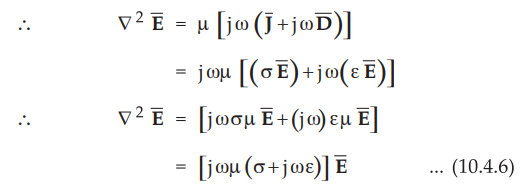
• In similar way, we can write another phasor equation as,

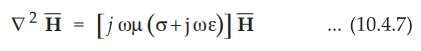
• The terms inside the bracket in equations (10.4.6) and (10.4.7) are exactly similar and represent the properties of the medium in which wave is propagating. The total bracket is the square of a propagation constant ɤ, hence we can rewrite equations (10.4.6) and (10.4.7) as,

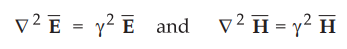
• So the propagation constant ɤ can be expressed interms of properties of the medium as,

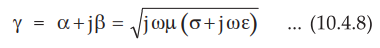
• The real and imaginary parts of ɤ are attenuation constant (α) and phase constant (β) and both can be expressed interms of the properties of the medium,

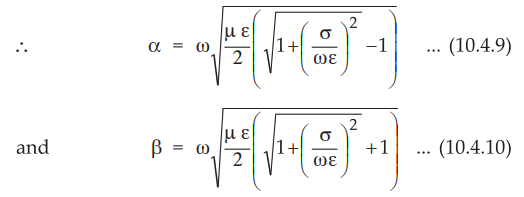
• The intrinsic impedance of a medium can be expressed interms of the properties of a medium and is given by,

• It can also be expressed in polar form as |ɳ| ∠ = θ where

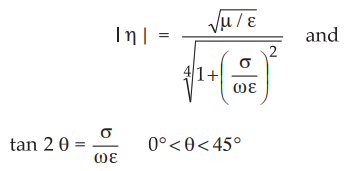
tan 2θ = σ/ωε 0^o ∠ θ ∠ 45^o

Ex. 10.4.1 The equation for the uniform plane wave travelling in free space is given in the phasor form. The electric field is given by,

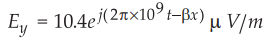Find

i) Direction of propagation of uniform plane wave,

ii) Phase velocity v,

iii) Phase constant β iv) Propagation constant ɤ,

v) Expression for the magnetic field in phasor form.

Sol.: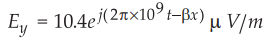  

i) Inspecting above expression, it is clear that   has only y component. Comparing above with standard equation,

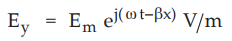
From the term β_x, it is clear that the wave travels in x direction.

Also, ω = 2π ×l0⁹ rad/s,

E_m = 10.4 × 10^-6 V/m

ii) For the free space, phase velocity is nothing but the velocity of light in free space.

          v = c = 3 × 10⁸ m/s

iii) For free space,

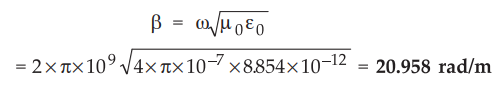
= 20.958 rad/m

iv) By property,

H_m = E_m/ η₀  For free space, η₀ = 377 Ω

H_m = 10.4 × 10^-6 / 377 = 0.0265 × 10^-6 A/m

As wave propagates in x-direction and   is in y-direction,  has to be z-direction. Hence expression for  is given by,

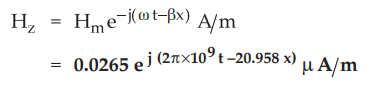
Example for Practice

Ex. 10.4.2 A uniform plane wave in free space is given by . Find : a) Direction of propagation of wave b) Angular frequency c) Wavelength d) Intrinsic impedance in free space e) Magnetic field intensity. 

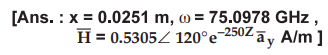
Review Questions

1. Derive the relationship between electric field and magnetic field. Derive the wave equation for magnetic field in phasor form.

AU : Dec.-lO, 13, Marks 16

2. Derive wave equations in phasor form. 

AU : Dec.-07, May-10, Marks 16

 3. Derive the EM wave equations in frequency domain and obtain the expressions for intrinsic impedance, and propagation constant for free space, conductor and dielectric media.

AU : May-13, Marks 16