EMT Solved Semester Question Paper 2018 Dec (2017 Reg)

DECEMBER - 2018

Electromagnetic Theory (25087)

Solved Paper

Sem – III [EEE]

Regulation - 2017

Time : Three Hours]     

[Maximum Marks : 100

Note : Answer ALL questions.

PART A - (10 × 2 = 20 Marks)

Q.1 Convert the given point (2, π/2, π / 3) in spherical coordinates into Cartesian coordinates.

(Refer Two Marks Q.55 of Chapter - 1)

Q.2 Determine the electric flux density at a distance of 20 cm due to an infinite sheet of uniform charge 20 pC/m2 lying on the z = 0 plane.

(Refer Two Marks Q.25 of Chapter - 3)

Q.3 Why the direction of electric field is always normal to equipotential surface ?

(Refer Two Marks Q.16 of Chapter - 4)

Q.4 Evaluate the capacitance of a single isolated sphere of 1.5 m diameter in free space.

(Refer Two Marks Q.40 of Chapter - 5)

Q.5 Give the force on a current element.

(Refer Two Marks Q.5 of Chapter - 8)

Q.6 Write down the steps to calculate inductance of various shapes.

(Refer Two Marks Q.39 of Chapter - 8)

Q.7    How does displacement current different from conduction current ?

(Refer Two Marks        Q.38  of Chapter - 9)

Q.8 Compare field theory with circuit theory.

(Refer Two Marks Q.30 of Chapter         - 9)

Q.9 Calculate the characteristic impedance of free space.

 (Refer Two Marks Q.8 of     Chapter - 10)

Q.10  State Poynting theorem.

(Refer Two Marks Q.48 of Chapter - 10)

 

PART B - (5 × 13 = 65 Marks)

Q.11 a) Express the vector  in Cartesian and cylindrical systems. Given 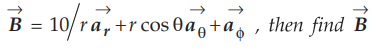 , then find B at (- 3, 4, 0) and (5, π/2, - 2).

(Refer example 1.13.3)

OR

b) i) Write down the expressions for gradient, divergence and curl in three co-ordinate systems.

(Refer sections 1.17, 1.16 and 1.18) [9]

ii) Point charges 5 nC and - 2 nC are located at (2, 0, 4) and (- 3, 0, 5), respectively. 1) Determine the force on a 1 nC point charge located at (1, - 3, 7) 2) Find the electric field intensity at (1, - 3, 7)

(Refer example 2.3.3)   [4]

Q.12 a) Define the following :

i) Electric potential and potential difference. (Refer sections 4.5)      [2]

ii) Uniform and non uniform fields with examples (Refer Two Marks Q.17 of Chapter - 4) [4]

iii) Dielectric polarization and dielectric constant (Refer sections 5.6)        [4]

iv) Capacitance and expression for energy stored in the capacitor (Refer sections 5.10 and 5.17)          [3] 

OR

b) i) State and derive electric boundary condition for (1) a dielectric to dielectric medium, (2) a conductor to dielectric medium and (3) free space to conductor. (Refer sections 5.8 and 5.9)          [10]

ii) Obtain Poisson's equation from the point form of Gauss's law in free space. (Refer section 6.2)   [3]

Q.13 a) Show by means of Biot-Savart's law that the flux density produced by an infinitely long straight wire carrying a current ‘T’ at any point ‘ρ’ normal  to the wire is given by µ₀µ_rI / 2πρ

OR

b) Derive the expressions for Biot-Savart law and ampere's circuit law from the concept of magnetic vector potential and also derive Poisson's equation for magneto static field.

(Refer example 7.12.5 and section 7.12.4) [13]

Q.14 a) Derive and explain the Maxwell's equations in integral and differential forms. (Refer section 9.5) [13]

OR

b) i) A parallel-plate capacitor with plate area of 5 cm² and plate separation of 3 mm has voltage 50 sin 103t V applied to its plates. Calculate the displacement current assuming Ɛ = 2Ɛ₀. (Refer example 9.3.9)

ii) Explain how the circuit equation for a series RLC circuit is derived from the field relations. (Refer section 9.9)

Q.15 a) Define wave. Derive the wave equation in terms of electric and magnetic fields for a conducting medium.

(Refer sections 10.1 and 10.2)

OR

b) A uniform plane wave of a damp soil has σ = 20×10⁻³ S/m, Ɛ = 2 Ɛ₀ is and μ = μ₀ having a frequency of

1 MHz.

i) Test the type of material

ii) Calculate the following

1) Attenuation constant

2) Phase constant

3) Propagation constant

4) Intrinsic impedance

5) Wave length

6) Velocity of propagation (Refer example 10.6.3) [13]

 

PART C - (1 × 15 = 15 Marks)

Q.16 a) Current carrying components in high-voltage power equipment must be cooled to carry away the heat caused by ohmic losses. A means of pumping is based on the force transmitted to the cooling fluid by charges in an electric field. The electro hydrodynamic (EHD) pumping is modelled in Fig. 1. 

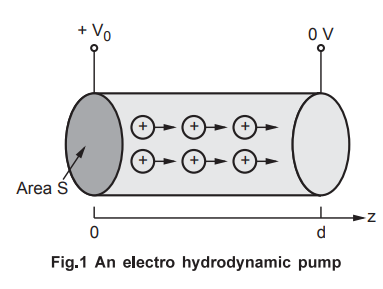
The region between the electrodes contains a uniform charge ρ₀, which is generated at the left electrode and collected at the right electrode. Calculate the pressure of the pump if Po = 25 mc/m3 and V₀ = 22 kV. [15]

(Refer example 6.4.8)

OR

b) Verify the divergence theorem for the function  over the surface of a quarter of a hemisphere defined by 0 < r < 3, 0 <θ < π/2, 0<ϕ <π/2.. (Refer example 1.16.4)