EMT Solved Semester Question Paper 2018 May (2017 Reg)

MAY - 2018

Electromagnetic Theory (40992)

Solved Paper

Sem – III [EEE]

Regulation - 2017

Time : Three Hours]     

[Maximum Marks : 100

Note : Answer ALL questions.

PART A - (10 x 2 = 20 Marks)

 

Q.1    Find the unit vector extending from the origin towards the point P(3, - 1, - 2).

(Refer Two Marks Q.54 of Chapter - 1)

Q.2 Determine the electric field intensity in free space if .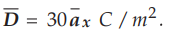

(Refer Two Marks Q.17 of Chapter - 3)

Q.3 Mention the properties of electric flux lines.

(Refer Two Marks Q.24 of Chapter - 3)

Q.4 State the electrostatic boundary conditions at the interface between two dielectrics.

(Refer Two Marks Q.20 of Chapter - 5)

Q.5 What is the total force acting on a moving charge, Q in the presence of both electric and magnetic fields.

(Refer Two Marks Q.3 of Chapter - 8)

Q.6 Compare magnetic scalar potential and magnetic vector potential.

(Refer Two Marks Q.31 of Chapter - 7)

Q.7 Define Reluctance and Permeability.

(Refer Two Marks Q.38 of Chapter - 8)

Q.8 Distinguish between conduction and displacement currents.

 (Refer Two Marks Q.38 of Chapter - 9)

Q.9 Mention the practical importance of 'Skin depth’.

(Refer Two Marks Q.60 of Chapter - 10)

Q.10  What is 'Standing Wave Ratio'?

(Refer Two Marks Q.36 of Chapter - 10)

 

PART B - (5 x 13 = 65 Marks)

 

Q.11 a) i) With neat diagrams, explain the spherical system with co-ordinates (R, θ, ϕ).

(Refer section 1.8)

ii) Apply Coulomb's law to find the electric field intensity at any point P due to a straight, uniformly charged wire of linear charge density + λ C/m. The point P is at a distance of 'h'm above the wire.

 (Refer section 2.6) [7]

OR

b) i) Explain the divergence of a vector field and divergence theorem.

(Refer sections 1.15 and 1.16)         [6]

ii) By mean of Gauss's law, determine the electric field intensity inside and outside a spherical shell of radius R. The shell contains a total charge Q uniformly distributed over the surface.

(Refer section 3.7.5)      [7]

Q.12 a)  i) Two point charges - 4 µC and 5 pC are located at (2, - 1, 3) and (0, 4,- 2 ) respectively. Find the potential at (1, 0, 1) assuming zero potential at infinity.

(Refer example 4.5.1)   [6]

ii) A parallel plate capacitor has a plate separation t. The capacitance with air only between the plates is C. When a slab of thickness t' and relative permitivity e' is placed on one of the plates, the capacitance is C' show

that C’/C = Ɛ’t / (t’ + Ɛ(t – t’) (Refer example 5.16.3)

C       (t+e(t -1)) r [7]

OR

i) Explain briefly the polarization in dielectrics.

(Refer section 5.6.1)      [6]

ii) Derive Laplace's and Poisson's equations from Gauss's law for a linear material medium. State the importance of these equations.

(Refer section 6.2)         [7]

Q. 13. a) i) By means of Biot-Savart's law, derive an expression for the magnetic field intensity at any point on the line through the centre at a distance 'h' from the centre and perpendicular to the plane of a circular loop of radius 'p' and carrying current'!'. (Refer section 7.7)  [6]

ii) An iron ring, 0.2 m in diameter and 10 cm² sectional area of the core, is uniformly wound with 250 turns

of wire. The wire carries a current of 4 A. The relative permeability of iron is 500. Determine the value of self-inductance and the stored energy. (Refer example 8.12.2)        [7]

OR

i) What is 'Magnetization ' ? Explain the classification of magnetic materials. (Refer sections 8.6 and 8.7) [6]

ii) What is the maximum torque on a square loop of 1000 turns in a field of uniform flux density of 1 Tesla 1

The loop has 10 cm sides and carries a current of 3 A. What is the magnetic moment of the loop ?

(Refer example 8.5.4) (Use B = 1)     [7]

Q. 14 a) An iron ring with a cross-sectional area of 3 cm2 and a mean circumference of 15 cm is wound with 250 turns of wire carrying a current of 0.3 A. The relative permeability of the ring is 1500. Calculate the flux established in the ring. (Refer example 8.9.1)       [13]

OR

i) Write a technical note on 'Transformer EMF and Motional EMF'. (Refer section 9.2)          [6]

ii) Describe the relationship between field theory and circuit theory. (Refer section 9.9) [7]

Q. 15 a) i) The electric field intensity associated with a plane wave travelling in a perfect dielectric medium is

given by Ex (z, t) = 10 cos(2π×10⁷t - 0.1πz) V/m. What is the velocity of propagation ?

 (Refer example 10.3.6) [6]

ii) Derive the Poynting theorem and state its significance.

 (Refer section 10.8)       [7]

OR

Write short notes on the following :   [4+4+5]

i) Plane waves in lossless dielectrics. (Refer section 10.5)

ii) Plane waves in free space. (Refer section 10.3)

iii) Plane waves in good conductors. (Refer section 10.7)

 

PART C - (1 × 15 = 15 Marks)

Q. 16 a) Step by step, develop a condition between

i) Conductor and dielectric. (Refer section 5.8)

ii) Dielectric and dielectric. (Refer section 5.9)      [15]

OR

b) From the basics, derive the expressions for Maxwell's equation in differential and integral form.

(Refer section 9.5)          [15]