Energy Conversion Via Electric Field

Energy Conversion Via Electric Field 

AU : Dec.-08, May-13

 • An electric field can be used as a coupling medium between electrical and mechanical systems for the electromechanical energy conversion. Such an energy conversion via electric field is analogous to an energy conversion via magnetic field. The charge in electric field is analogous to the flux linkages while the voltage is analogous to the current in a magnetic field. Let us use energy and co-energy methods to obtain the expression for the force.

1. Electric Field Energy Stored

• A parallel plate condenser with a fixed and movable plates is an example of energy conversion device using electric field as a coupling medium. This is called singly excited electric field energy conversion device. The device is shown in the Fig. 2.8.1.

• A current source is used to feed the condenser. The leakage current of the condenser is represented by the conductance G. This means that the electric field of the condenser is conservative i.e. all the energy supplied is recoverable from the device.

• When the current source is connected to a condenser, the charge q and current i flow into the condenser. The differential electrical energy input is,

dW_e = v i dt = v da ... dq = i dt

While the mechanical work done in time dt by the force F_f is,

dW_m = F_f dx

where dx is the movement of the movable plate in the direction of F_f in time dt. Neglecting the losses, from the basic energy balance equation, we can write,

dW_e = dW_m + dW_f

ஃ  v d_q = F_f dx+dW_f   ... (2.8.1)

Let us assume that the movable plate is held fixed in position x then dx = 0 hence dW_m = 0.

dWf = v dq = Differential energy stroed

Now the voltage v is constant while the charge increases form 0 to q hence,

For a condenser v and q are linearly related given by,

The capacitance of the parallel plate capacitor with a distance of (x0 – x) between the plates is given by,

C = ε₀ A / (x₀ – x) … (2.8.5)

where A = cross-sectional area of plate in m²

ε₀ = Permittivity of free space = 8.854 × 10^-12 F/m

Thus W_f is function of two independent variable q and x

W_f (q,x) = 1/ 2 q²/C(x)

The equation (2.8.6) suggests that, the electric field energy can be changed,

1. Electrically by changing the charge q.

2. Mechanically by changing the distance x with moving plate.

Where D = ε₀ E = Electric flux density in C/m²

E = Electric field intensity or potential gradient in V/m.

2. Analysis of Energy Conversion

• Let the movable plate is allowed to move under the influence of force F_f

Now the v and x are independent variables, to satisfy above equation, the coefficient of dv must be zero.

But q and x are independent variables hence the coefficient of dq must be zero in the equation (2.8.15)

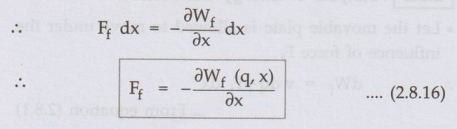
3. Co-energy Calculations

• For a linear case like capacitor the variation of a with v is shown in the Fig. 2.8.2.

The area OCAO is the co-energy W’_f

Key Point : The field energy in equation (2.8.16) must be expressed in q and x while the co-energy in equation (2.8.14) must be expressed in v and x.

Ex. 2.8.1 Find an expression for the force per unit area between the plates of a parallel plate condenser interms of the electric field intensity. Use both the energy and co-energy methods. Find the value of the force per unit area when E = 3x10⁶ V/m, the breakdown strength of air. AU : Dec.-08, May-13, Marks 16

Sol. : Consider a parallel plate condenser shown in the Fig. 2.8.3.

For such an arrangement, the field energy is given by,

Thus by both the methods, the force per unit area is same.

Review Question

1. Derive the expression for the force between the plates of a parallel plate capacitor using energy and co-energy method.