Energy Density in the Electrostatic Fields

Energy Density in the Electrostatic Fields

• It is seen that, when a unit positive charge is moved from infinity to a point in a field, the work is done by the external source and energy is expended. If the external source is removed then the unit positive charge will be subjected to a force exerted by the fieldp and will be moved in the direction of force. Thus to hold the charge at a point in an electrostatic field, an external source has to do work. This energy gets stored in the form of potential energy, when the test charge is hold at a point in a field. This is analogous to the water lifted at a height h and stored in a tank. Then it has a potential energy. When external source is removed, the potential energy gets converted to a kinetic energy. In this section, the expression of such a potential energy is derived.

• Consider an empty space where there is no electric field at all. The charge Q₁ is moved from infinity to a point in the space say P₁ This requires no work as there is no   present. Now the charge Q₂ is to be placed at point P₂ in the space as shown in the Fig. 4.13.1. But now there is an electric field due to Q₁ and Q₂ is required to be moved against the field of Q_1. Hence the work is required to be done.

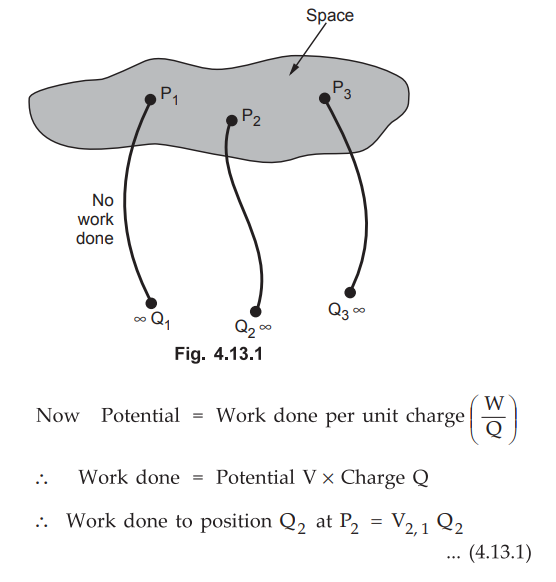
Work done per unit charge

where          V_{2 ,1} = Potential at P₂ due to P₁

• Now let charge Q₃  is to be moved from infinity to P₃. There are electric fields due to Q₁ and Q₂. Hence total work done is due to potential at P₃ due to charge at P₁ and potential at P₃ due to charge at p₂.

.•. Work done to position Q₃ at

P₃ = V₃, ₁ Q₃ + V_3,2 Q₃ …. (4.13.2)

Thus for charge Q_n to be placed at P_n, we can write,

Work done to po sition Q_n at

P_n = V_n,1 Q_n + V _n,2 Q _n …. (4.13.3)

• Hence the total work done in positioning all the charges is,

W_E = Q₂ V_2,1 + Q ₃ V_3,1 + Q₃ V_{3, 2} + .... (4.13.5)

• The total work done is nothing but the potential energy in the system of charges hence denoted as W_E.

• If charges are placed in reverse order we can write,

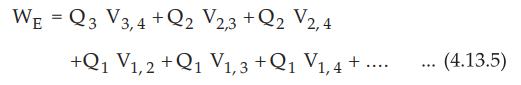
In this expression Q_n is placed first, then Q_n-1... then Q₄,Q₃,Q₂ and finally Q₁.

Adding (4.13.4) and (4.13.5),

• Each sum of the potentials is the total resultant potential due to all the charges except for the charge at the point at which potential is obtained.

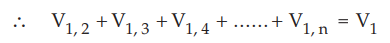
• This is potential at P₁ where Q₁ is placed due to all other charges Q₂,Q₃,... Q_n

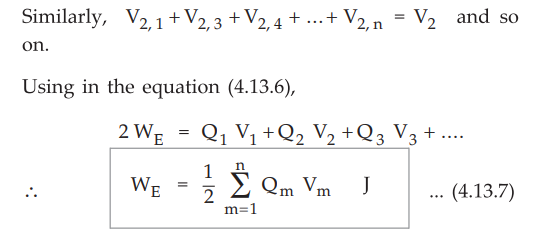
• This is the potential energy stored in the system of n point charges.

• It instead of point charges, the region has continuous charge distributions then summation in equation (4.13.7) becomes integration.

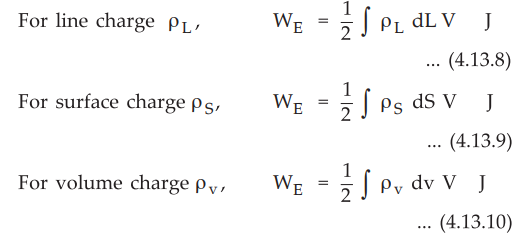
1. Energy Stored interms of 

• Consider the volume charge distribution having uniform charge density ρv C/ m³. Hence the total energy stored is given by the equation (4.13.10) as,

• According to Maxwell's first equation,

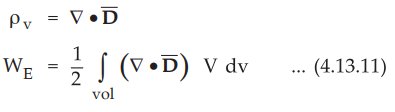
• For any vector A and scalar V there is vector identity,

• According to divergence theorem, volume integral can be converted to closed surface integral if closed surface totally surrounds the volume.

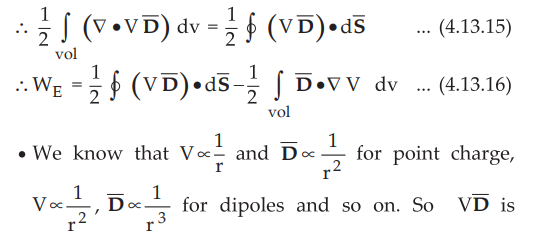
proportional to at least 1/r³ while dS varies as r². Hence total integral varies as 1/r. As surface becomes very large, r → ∞ and 1/r   0. Hence closed surface integral is zero in the equation (4.13.16).

• This is called energy density in the electric field having units J /m³. If this is integrated over the volume, we get total energy present.

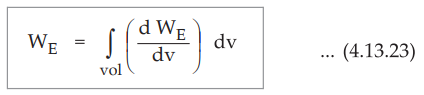
Ex. 4.13.1 The electric field between two concentric cylindrical conductors at r = 0.01m and r = 0.05 m is given by . Find the energy stored in a 50 metre length. Assume free space.

Ex. 4.13.2 If V = x – y + xy + 2z V, find  at (1, 2, 3) and the energy stored in a cube of side 2 m centered at the origin.

AU : May-19, Marks 13

Sol. :

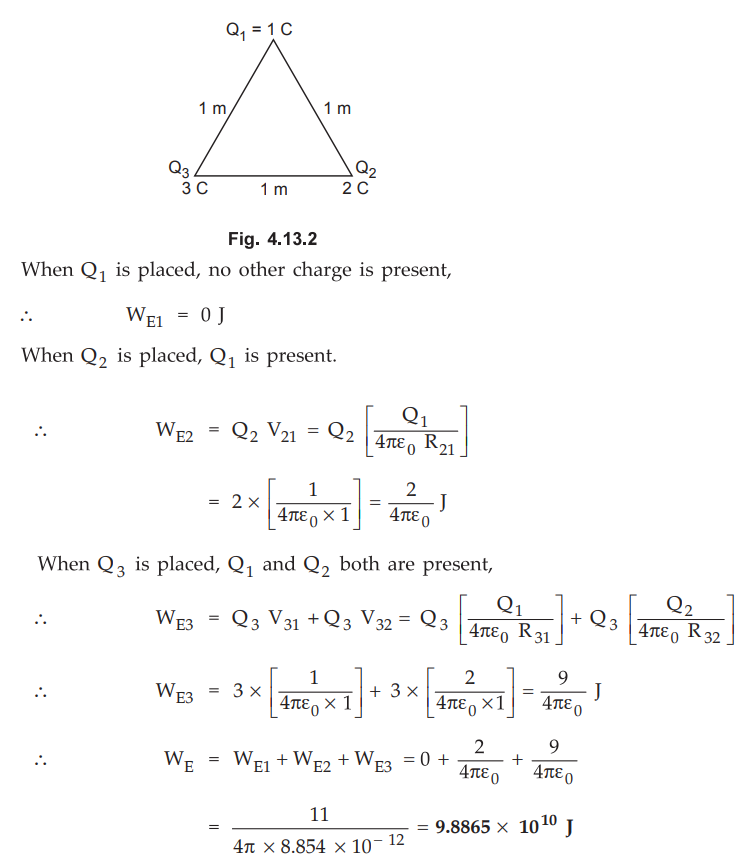
Ex. 4.13.3 Three point charges 1, 2, 3 coulombs are situated in free space at the corners of an equilateral triangle of side 1 m, Find the energy stored in the system.

AU : May-08, Marks 8

Sol. : The charges existing at the comers of an equilateral triangle are shown in the Fig. 4.13.2.

Ex. 4.13.4 The potential field in free space is given by,

V = 50/r , a ≤ r ≤ b (spherical)

i) Show that ρv = 0 for a < r < b

ii) Find the energy stored in the region a < r < b.

Sol. :

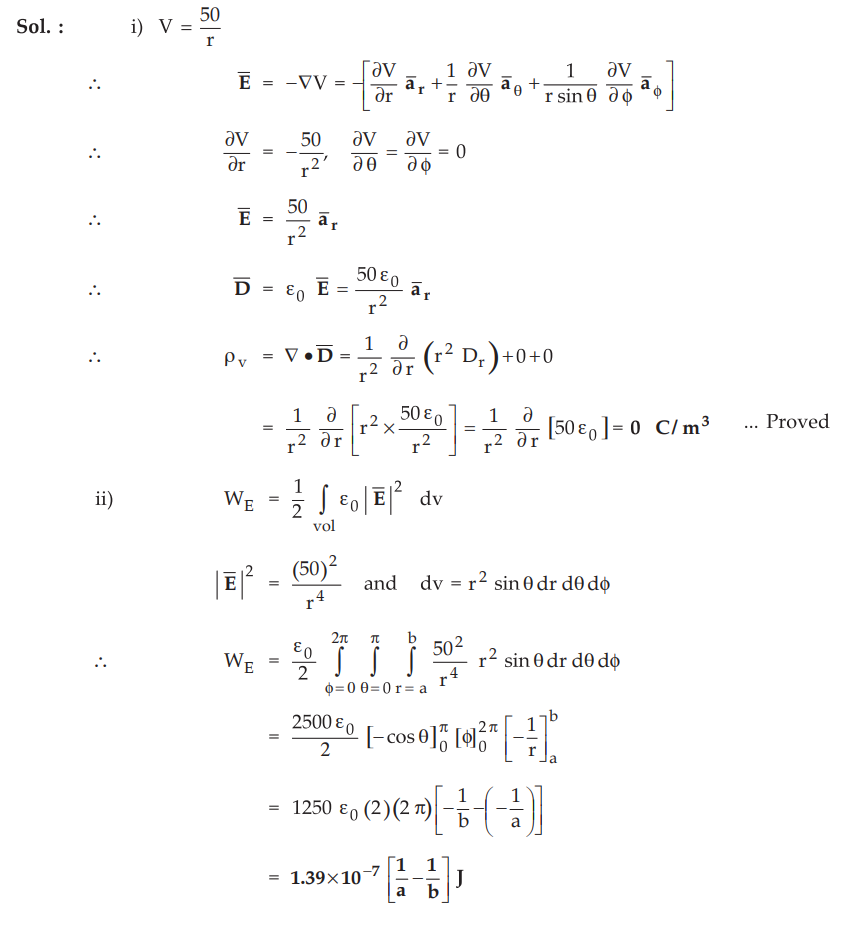
Examples for Practice

Ex. 4.13.5 Point charges Q₁ = 1 nC, Q₂ = - 2 nC, Q₃ = 3 nC and Q₄ = - 4 nC are placed one by one in the same order at (0,0,0), (1,0,0), (0,0,-1) and (0,0,1) respectively. Calculate the energy in the system when all charges are placed. 

[Ans.68.178 J]

Ex. 4.13.6 Find the potential energy stored in the following free space charge configurations,

i) A charge Q at each corner of an equilateral triangle of sides d.

ii) A charge Q at each comer of a square of side'd'.

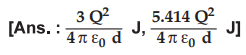
Ex. 4.13.7 IfV = x- y + xy + zV, find  at (1, 2, 4) and the electrostatic energy stored in a cube of side 2 m centered at the origin.

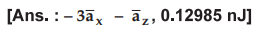
Ex. 4.13.8 Find the stored energy in a system of four identical charges Q = 4 nC at the corners of a square of 1 m on a side.

[Ans.: 0.7785 µJ]

Ex. 4.13.9 A pair of 200 mm long concentric cylindrical conductors of radius 50 and 100 mm is filled with a dielectric of £ = 10 EQ. A voltage is applied between the conductors to establish an electric field,

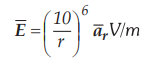 between cylinders. Calculate energy stored.

[Ans.: 5.691 × 10¹³ J]

Ex. 4.13.10 V = r2 z sin ϕ, calculate the energy within the region defined by

1 < r < 4, - 2 < z < 2 and

0 < ϕ < π/3

[Ans.: 6.6735 nJ]

Review Question

1. Derive the expression for energy stored and energy density in electrostatic fields.

AU : May-06, 10, Dec.-12, 13, Marks 8