Energy Stored in the Magnetic Field

Energy Stored in the Magnetic Field

AU : May-10, Dec.-12, 15

• We know that energy is required to establish flux i.e. magnetic field but it is not required to maintain it. This is similar to the fact that the energy is required to raise the water through a certain height (h) which is 'mgh' joules. But energy is not required to maintain the water at height 'h'. This energy 'mgh' gets stored in it as its potential energy and can be utilized for many purposes.

Key Point : The energy required to establish magnetic field then gets stored into it as a potential energy. This energy can be recovered when magnetic field established, collapses.

This can be explained as below.       

 • Consider a solenoid, the current through which can be controlled with the help of switch S, resistance R shown in the Fio. 126.1.

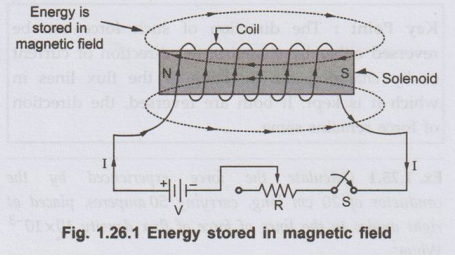
• Initially switch 'S' is open, so current through coil, I is zero. When switch is closed, current will try to built its value equal to I. Neglect the resistance of coil.    

• It will take some time to increase the current from 'zero' to 'I' say 'dt' seconds.      

• In the mean time, flux linkages associated with the coil will change, due to which there will be self induced e.m.f. in the coil whose value is given by,           

e = -L dI/dt

• So at every instant, coil will try to oppose the increase in the current. To overcome this opposition, supply has to provide the energy to the circuit. This is nothing but the energy required to establish the current i.e. magnetic field or flux around the coil.

• Once current achieves its maximum value 'I' then change in current stops. Hence there can not be any induced e.m.f. in the coil and no energy will be drawn from the supply. So no energy is required to maintain the established flux. This is because, induced e.m.f. lasts as long as there is change in flux lines associated with the coil, according to Faraday's law.

Key Point : Now the energy which supply has provided, gets stored in the coil which is energy stored in the magnetic field, as its potential energy.

• When current is again reduced to zero by opening the switch then current through the coil starts decreasing and flux starts decreasing. So there is induced e.m.f. in the coil according to Faraday's law. But as per Lenz's law it will try to oppose cause producing it which is decrease in current. So this induced e.m.f. now will try to maintain current to its original value. So instantaneously this induced e.m.f. acts as a source and supplies the energy to the source. This is nothing but the same energy which is stored in the magnetic field which gets recovered while field collapses. So energy stored while increase in the current is returned back to the supply when current decreases i.e. when field collapses.

Key Point : The energy which is stored in the coil earlier is returned back to the supply. No additional energy can exist as coil can not generate any energy.

The expression for this energy stored is derived below.

1. Expression for Energy Stored in the Magnetic Field

Let the induced e.m.f. in a coil be,

 e = - L/dI/dt

• This opposes a supply voltage. So supply voltage 'V' supplies energy to overcome this, which ultimately gets stored in the magnetic field.        

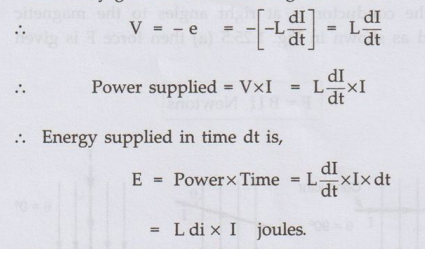
• This is energy supplied for change in current of dI but actually current changes from zero to I.

 ஃ Integrating above total energy stored is,

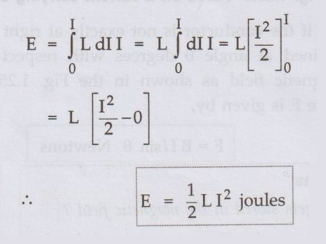
2. Energy Stored Per Unit Volume (Energy Density)

• The above expression for the energy stored can be expressed in the different form as,

• In case of inductive circuit when circuit is opened with the help of switch then current decays and finally becomes zero. In such case energy stored is recovered and if there is resistance in the circuit, appears in the form of heat across the resistance. 

• While if the resistance is not present then this energy appears in the form of an arc across the switch, when switch is opened. 

• If the medium is air, µ_r = 1 hence µ = µ₀ must be used in the above expressions of energy.

Ex. 1.26.1 A coil is wound on an iron core to form a solenoid. A certain current is passed through the coil which is producing a flux of 40 µWb. The length of magnetic circuit is 75 cm while its cross-sectional area is 3 cm². Calculate the energy stored in the circuit. Assume relative permeability of iron as 1500.       

Sol. :

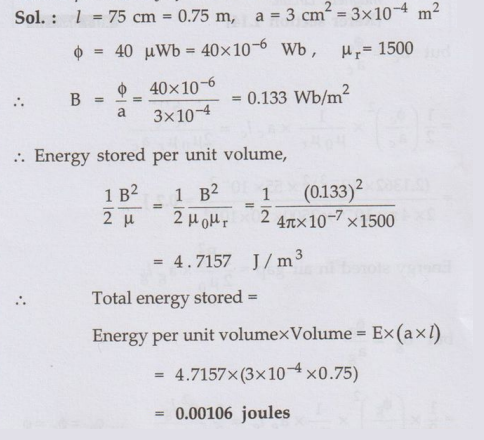
Ex. 1.26.2 In the magnetic circuit considered in the example 1.31. if µ_r = 2500 then determine,   a) Energy stored in the core and air gap if exciting current is 5 A.b) Excitation current to produce a sinusoidally varying flux of 0.5 sin 314 t.c) Inductance of the coil.

Sol. :         

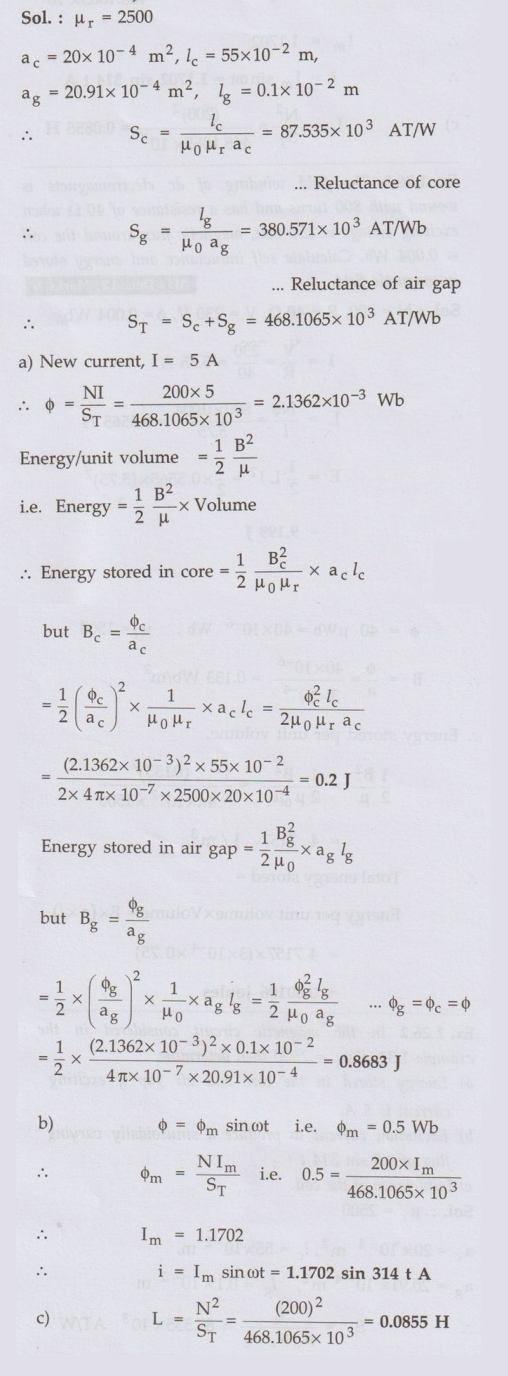
Ex. 1.26.3 The field winding of de electromagnets is wound with 800 turns and has a resistance of 40 Ω when exciting voltage is 230 volt, magnetic flux around the coil is 0.004 Wb. Calculate self inductance and energy stored in magnetic field.

AU : Dec.-12, Marks 6 

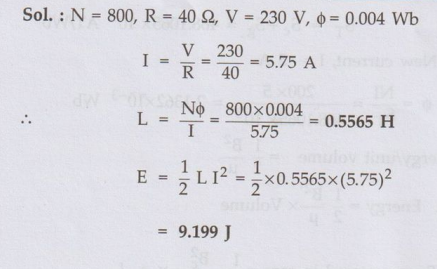
Review Questions

1. How energy gets stored in the magnetic field ?

2. Derive the expression for energy stored in the magnetic field.

3. Derive the expression for the energy density in the magnetic field. AU : May-10, Dec.-15, Marks 6

4. An iron cored toroid of relative permeability 980 has a mean length of 120 cm and core area of 100 mm². A current of 0.3 A establishes a flux of 40 µWb, calculate i) The number of turns of coil ii) Self inductance iii) Energy stored in magnetic field. [Ans. : 1300 turns, 0.1733 H, 7.8 x10-3 joules, 7.8 x10-3 J]