Equipotential Surfaces

 Equipotential Surfaces

• In an electric field, there are many points at which the electric potential is same. This is because, the potential is a scalar quantity which depends on the distance between the point at which potential is to be obtained and the location of the charge. There can be number of points which can be located at the same distance from the charge. All such points are at the same electric potential. If the surface is imagined, joining all such points which are at the same potential, then such a surface is called equipotential surface.

Key Point : An equipotential surface is an imaginary surface in an electric field of a given charge distribution, in which all the points on the surface are at the same electric potential.

• The potential difference between any two points on the equipotential surface is always zero. Thus the work done in moving a test charge from one point to another in an equipotential surface is always zero. There can be many equipotential surfaces existing in an electric field of a particular charge distribution.

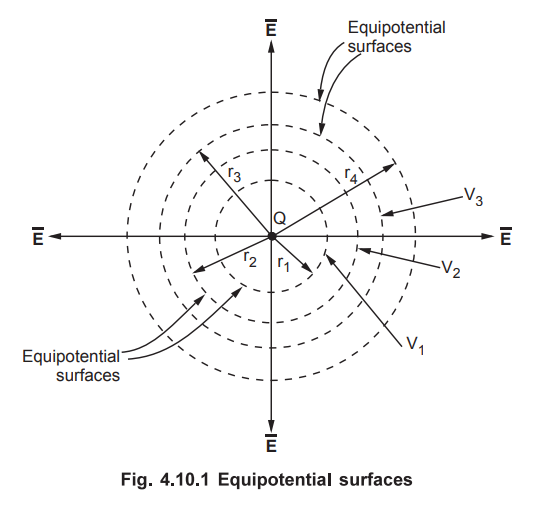
• Consider a point charge located at the origin of a sphere. Then potential at a point which is at a radial distance r from the point charge is given by,

V = Q / 4πƐ₀r

• So at all points which are at a distance r from Q, the potential is same and surface joining all such points is equipotential surface.

• Similarly at r = r₁ r = r₂  ... there exists other equipotential surfaces, in an electric field of point charge, in the form of concentric spheres as shown in the Fig. 4.10.1.

• It can be noted that V is inversely proportional to distance r. Thus V₁ at equipotential surface at r = r₁ is highest and it goes on decreasing, as the distance r increases. Thus V₁ > V₂ > V₃ >  As we move away from the charge, the  decreases hence potential of equipotential surfaces goes on decreasing. While potential of equipotential surfaces goes on increasing as we move against the direction of electric field.

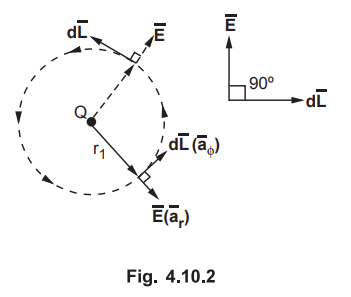
 • For a uniform field  , the equipotential surfaces are perpendicular to   and are equispaced for fixed increment of voltages. Thus if we move a charge along a circular path of radius г₁ as shown in   direction, then work done is zero. This is because   and  are perpendicular. Thus   and equipotential surface are at right angles to each other.

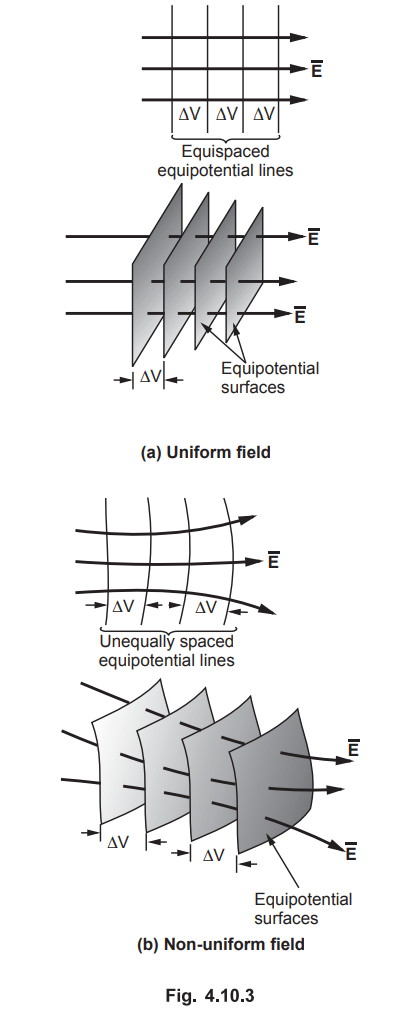
• For a nonuniform field, the field lines tends to diverge in the direction of decreasing  Hence equipotential surfaces are still perpendicular to E but are not equispaced, for fixed increment of voltages. The equipotential surfaces for uniform and nonuniform field are shown in the Fig. 4.10.3 (a) and (b).

Review Question

1. Explain the concept of equipotential surfaces.