Equivalent Circuit of Practical Op-amp

Equivalent Circuit of Practical Op-amp

The circuit which represents op-amp parameters in terms of physical components, for the analysis purpose is called equivalent circuit of an op-amp. The equivalent circuit of an op-amp is shown in the Fig. 2.11.1.

The circuit shows the op-amp parameters like input resistance, output resistance, the open loop voltage gain in terms of circuit components like R_in, R_o etc. The op-amp amplifies the difference between the two input voltages.

V_o = A_OLV_d = A_OL(V₁ - V₂)

where A_OL = Large signal open loop voltage gain.

V_d = Difference voltage V₁ - V₂.

V₁ = Noninverting input voltage with respect to ground.

V₂ = Inverting input voltage with respect to ground.

R_i = Input resistance of op-amp.

R_o = Output resistance of op-amp.

The output voltage is directly proportional to the difference voltage V_d.

It is to be noted that the op-amp amplifies difference voltage and not the individual input voltages. Thus the output polarity gets decided by the polarity of the difference voltage V_d.

The voltage source A_OLV_d is the Thevenin's equivalent voltage source while Ro is the Thevenin's equivalent resistance looking back into the output terminals.

The equivalent circuit plays an important role in analysing various op-amp applications as well as in studying the effects of feedback on the performance of op-amp.

1. Practical Op-amp Characteristics

The characteristics of an ideal op-amp can be approximated closely enough, for many practical op-amps. But basically the practical op-amp characteristics are little bit different than the ideal op-amp characteristics.

The various characteristics of a practical op-amp can be described as below.

a) Open loop gain : It is the voltage gain of the op-amp when no feedback is applied. Practically it is several thousands.

b) Input impedance : It is finite and typically greater than 1 MQ. But using FETs for the input stage, it can be increased upto several hundred MQ.

c) Output impedance : It is typically few hundred ohms. With the help of negative feedback, it can be reduced to a very small value like 1 or 2 ohms.

d) Bandwidth : The bandwidth of practical op-amp in open loop configuration is very small. By application of negative feedback, it can be increased to a desired value.

e) Input offset voltage : Whenever both the input terminals of the op-amp are grounded, ideally, the output voltage should be zero. However, in this condition, the practical op-amp shows a small non zero output voltage. To make this output voltage zero, a small voltage in millivolts is required to be applied to one of the input terminals. Such a voltage makes the output exactly zero. This d.c. voltage, which makes the output voltage zero, when the other terminal is grounded is called input offset voltage denoted as Vios. How much voltage, to which terminal and with what polarity, to be applied, is specified by the manufacturer in the datasheet. The input offset voltage depends on the temperature. The concept of input offset voltage is shown in the Fig. 2.11.2.

The V_ios can be positive or negative hence absolute value of the V_ios is mentioned in the data sheet.

The smaller the value of Vios , better is the matching of the input terminals.

The input offset voltage depends on the temperature.

Many time voltage to one of the input terminals is applied with the proper polarity so as to null the output, keeping other input terminal grounded. For ideal op-amp, Vios is zero, hence practical op-amp model is generally shown as in the Fig. 2.11.3 with the indication of the input offset voltage. For op-amp 741 C the input offset voltage is 6 mV.

f) Input bias current : The average value of the two currents flowing into the op-amp input terminals is called input bias current and denoted as I_b. It is shown in the Fig. 2.11.4.

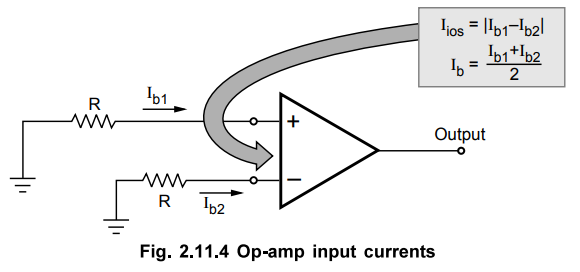
Mathematically it is expressed as,

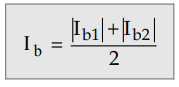
g) Input offset current : It is seen that the input stage of the op-amp is the dual input differential amplifier and the input terminals are the base terminals of the two transistors as shown in the Fig. 2.11.5. Hence the input currents of op-amp are the base currents of the two transistors Q₁ and Q₂ used in the input stage. Ideally, Q₁ and Q₂ must be perfectly matched and two base currents must be equal. But practically the two input base currents differ by small amount.

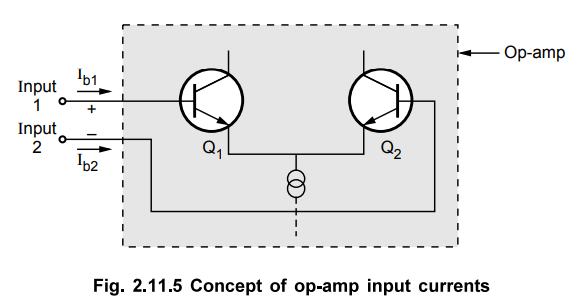
The algebraic difference between the currents flowing into the two input terminals of the op-amp is called input offset current and denoted as I_ios

Mathematically it is expressed as,

I_ios = | I_b1 - I_b2|

Where I_b1 = Current entering into noninverting input terminal

and I_b2 = Current entering into inverting input terminal

Ideally I_ios is zero while for op-amp 741C, maximum value of I_ios is 200 nA.

This current is responsible to produce the output though input terminals are grounded.

Example 2.11.1 If the base currents for the emitter coupled transistors of a differential amplifier are 18 μA and 22 μA, determine

i) Input bias current  ii) Input offset current for an op-amp.

Solution: The two input base currents are, I_bl = 18 μA and I_b2 = 22 μA

i) The input bias current is

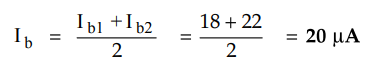
ii) The input offset current is

I_ios = |I_b1 - I_b2| = |18 – 22| = 4µA

Example 2.11.2 For a particular op-amp, the input offset current is 20 nA while input bias current is 60 nA. Calculate the values of two input bias currents.

Solution :

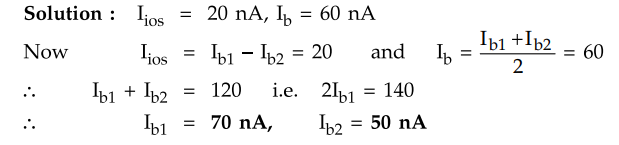
Review Questions

1. Draw and explain practical op-amp equivalent circuit.

2. Explain the practical characteristics of op-amp.

3. Define the following for a practical op-amp : i) Input offset voltage ii) Input offset current iii) Input bias current.