Equivalent Circuit of Single Phase Induction Motor

Equivalent Circuit of Single Phase Induction Motor AU : April-01, Dec.-05, 15, 17, May-17

The double revolving field theory can be effectively used to obtain the equivalent circuit of a single phase induction motor. The method consists of determining the values of both the fields clockwise and anticlockwise at any given slip. When the two fields are known, the torque produced by each can be obtained. The difference between these two torques is the net torque acting on the rotor.

Imagine that the single phase induction motor is made up of one stator winding and two imaginary rotor windings. One rotor is rotating in forward direction i.e. in the direction of rotating magnetic field with slip s while other is rotating in backward direction i.e. in direction of oppositely directed rotating magnetic field with slip 2 - s.

To develop the equivalent circuit, let us assume initially that the core loss is absent.

 

1. Without Core Loss

Let the stator impedance be Z Ω

Z = R₁ + j X₁

where R₁ = Stator resistance

X₁ = Stator reactance

and X₂ = Rotor reactance referred to stator

R₂ = Rotor resistance referred to stator

Hence the impedance of each rotor is r₂ + j x₂ where

X₂ =  X₂ / 2

The resistance of forward field rotor is r₂ / s while the resistance of backward field rotor is r₂ / (2 - s ) The r9 r₂ value is half of the actual rotor resistance referred to stator.

As the core loss is neglected, R₀ is not existing in the equivalent circuit. The X₀ is half of the actual magnetising reactance of the motor. So the equivalent circuit referred to stator is shown in the Fig. 8.9.1.

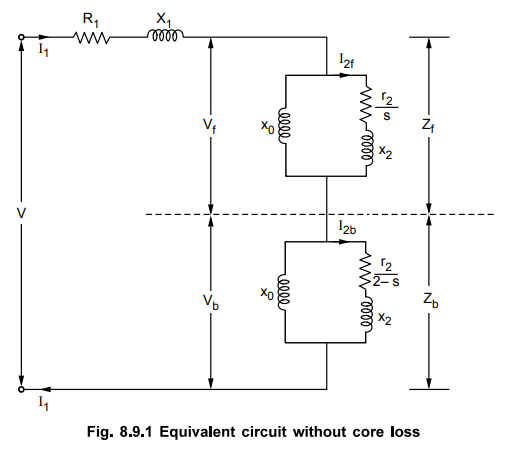
Now the impedance of the forward field rotor is Z_f which is parallel combination of (0 + j X₀) and (r₂/s) + j x₂.

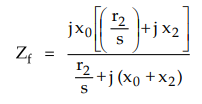
While the impedance of the backward field rotor is Z_b which is parallel combination of (0 + j x₀) and (r₂ 2-s ) + j x₂.

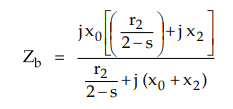
Under standstill condition, s = 1 and 2 - s = 1. Hence Z_f = Z_b and V_f = V_b. But in the running condition, Vf becomes almost 90 to 95 % of the applied voltage.

Z_eq = Z₁ + Z_f + Z_b = Equivalent impedance

Let I_2f = Current through forward rotor referred to stator

and I_2b = Current through backward rotor referred to stator

 

2. With Core Loss 

If core loss is to be considered then it is necessary to connect a resistance r0 in parallel with x₀, in an exciting branch of each rotor r₀ is half the value of actual core loss resistance. Thus the equivalent circuit with core loss can be shown as in the Fig. 8.9.2.

Let Z_of = Equivalent impendanve of exciting branch in forward rotor

= r₀ || (j x₀ )

And Z_ob  = Equivalent impendanve of exciting branch in backward rotor

= r₀ || (j x₀ )

Z_f = Z_of || (r₂ / s + j x₂ )

All other expressions remain same as stated earlier in case of equivalent circuit without core loss. 

 

Example 8.9.1 A 600 W, 230 V, 50 Hz, 6 pole, single phase induction motor has following parameters :

Resistance of main stator winding = 3 Ω

Reactance of main stator winding = 4.15 Ω

Reactance of magnetising branch referred to stator = 107 Ω

Rotor resistance referred to stator at standstill  =  6.2 Ω

Rotor reactance referred to stator at standstill = 2.2 Ω

The core losses are 75 W while mechanical losses are 25 W. The motor is operating with 5 % slip. Calculate,

i) Input current ii) Power factor         iii) Gross power iv) Shaft power v) Efficiency.

Solution :

The given values are,

 

Example 8.9.2 A 220 V, 50 Hz, 6 pole single phase induction motor has the following parameters V1 = 3.04 Ω ,X1 = 4.2 Ω, Xm = 105.6 Ω, r2 = 6.26 Ω, X'2 = 2.12 Ω. It is operating at 5 %. Find the forward, backward and net torque in synchronous watts. AU : April-01, Marks 10

Solution :  

 

Example 8.9.3 A 2 pole 50 Hz single phase induction motor has an effective rotor resistance and leakage reactance of 05 Ω each. If it is running at 2600 r.p.m. Find

i) Frequencies of rotor current components.

ii) Relative magnitudes of forward and backward fluxes. Neglect magnetizing current and stator impedance.

Solution :

Neglecting magnetizing current and stator impedance, the equivalent circuit is shown in the Fig. 8.9.4.

 

Examples for Practice

Example 8.9.4 A 230 V, 50 Hz, 4-pole single-phase induction motor has the following equivalent circuit impedances.

R_lm = 2.2 Ω,             R'2 = 4.5 Ω

X_lm = 3.1 Ω,              X'2 = 2.6 Ω,    X_m = 80 Ω

Friction, windage and core loss = 40 W

For a slip of 0.03 pu, calculate i) Input current ii) Power factor iii) Developed power iv) Output power v) Efficiency.

 [Ans.: i) 5.684 ∠- 6096, ii) 0.4854 lagging, iii) 479.43 W, iv) 439.43 W, v) 634.5731 W, % n = 69.248 %]

Example 8.9.5 The constants of a quarter H.P., 230 V, 50 Hz, 4 pole single phase induction motor are as follows : stator resistance - 10 Ω , stator reactance = 12.8 Ω, magnetizing reactance = 258 Ω , rotor resistance referred to stator - 11.65 Ω . 

Rotor reactance referred, to stator - 12.8 Ω .

The total load is such that the machine runs at 3 % slip, when the voltage is at 210 V. The iron losses are 35.5 W at 210 V. If the mechanical losses are 7 W, calculate,

a) Input current b) Power developed c) Shaft power d) Efficiency.

[Ans.: a) 1.8585 ∠- 53.65° A, b) 166.72 W, c) 159.72, d)% ƞ = 63.04 %]

Example 8.9.6 A 220 V, 6-pole, 50 Hz single winding single phase induction motor has the following equivalent circuit parameters as referred to the stator Rlm = 3 Ω

R_lm = 5 Ω      X_lm = 5 Ω

R₂ = 1.5 Ω    X₂ = 2 Ω

Neglect the magnetizing current, when the motor runs at 97 % of the synchronous speed, compute the ratio Emf/Emb and ratio Tf/ Tb'.

[Ans.:Emf / Emb = 23.38, Tf/ Tb'= 65.668]

Example 8.9.7 A 125 W, 4 pole 110 V, 50 Hz single phase induction motor delivers rated output at a slip of 6 %. The copper loss at full load is 25 watts. Calculate the full load efficiency and the rotor copper loss caused by the backward field. Rotational losses may be assumed to be 25 watts. Neglect stator copper loss. 

[Ans.: % ƞ = 78.33 %, 14.96 W]

Review Questions

1. Draw and explain the equivalent circuit diagram of a single phase induction motor.

2. Develop the equivalent circuit of a single phase induction motor.