Transmission and Distribution: Unit II: (a) Modelling and Performance of Transmission Lines
Equivalent T and π Network of Long Transmission Line
Modelling and Performance of Transmission Lines
These methods are said to be nominal methods as they do not take into account the actual conditions i.e. instead of taking the parameters of the lines as uniformly distributed they are considered to be concentrated or lumped at one point in the transmission line network.
Equivalent T and π Network
of Long Transmission Line
In case of analysis of medium
transmission line, we have used nominal T and nominal n method. These methods
are said to be nominal methods as they do not take into account the actual
conditions i.e. instead of taking the parameters of the lines as uniformly
distributed they are considered to be concentrated or lumped at one point in
the transmission line network.
For transmission line of lengths more
than 160 km, the parameters of the line are considered to be distributed and
voltages and currents at sending end are obtained by rigorous method as,

We will now derive equivalent T and
equivalent n networks for such long lines. Let us first consider equivalent T
network.
1. Equivalent T Representation of Long Transmission Line
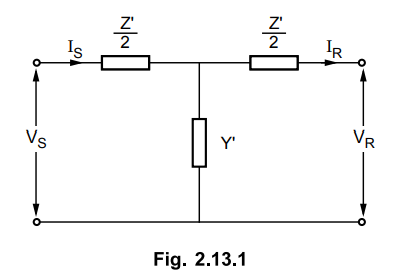
Consider the following network shown in
Fig. 2.13.1 to determine the equivalent-T network.
From analysis of this network carried
out earlier we have,
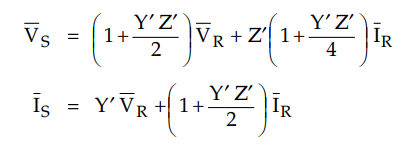
Comparing above equations with those obtained
for along transmission line using rigorous analysis.
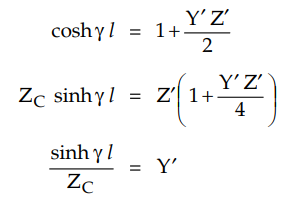
Consider the shunt branch of
equivalent-T network as shown in Fig. 2.13.1.
Its admittance is given as,
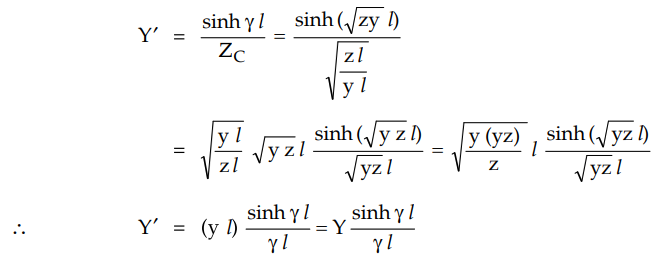
This indicates that the shunt branch of
equivalent T can be obtained by multiplying the shunt branch of nominal T
(lumped shunt admittance) by the factor (sin ɤ l / ɤ l)
Now let us determine series impedance of
the equivalent-T network.
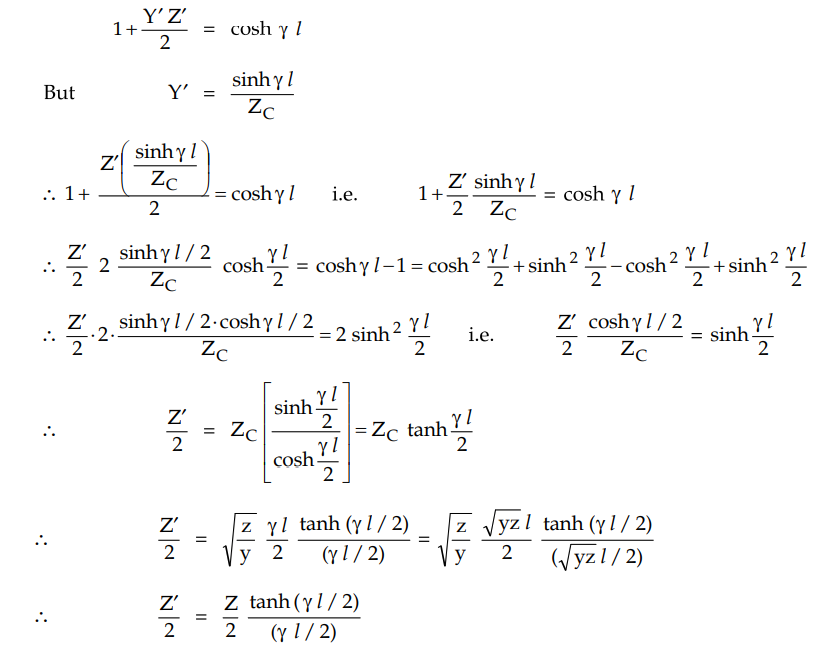
This indicates that the series branch of
the equivalent-T network can be determined by multiplying the series branch of
the nominal-T (lumped series impedance) network with factor tanh (ɤ l /
2) / (ɤ l / 2). The equivalent network is shown in Fig. 2.13.2.
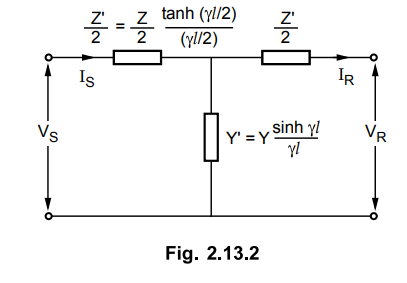
It can be seen that for small values of
y l , the ratio of tanh(y l / 2)/(y l / 2) and (sinh ɤ l) / ɤ l
almost approach unity and the nominal circuits represent the medium length
lines quite accurately.
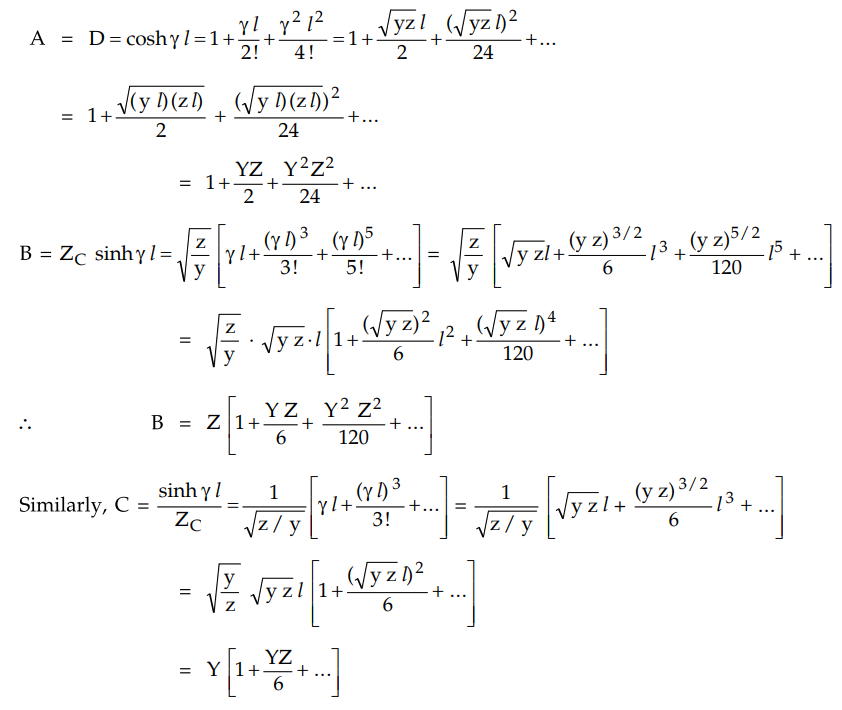
By taking into consideration only the
first order terms, we can get the A, B, C, D parameters of nominal-T or n
representation. Also, it can be assumed that
Y2Z / 6 ≈ Y2Z / 4 for small Y2.
2. Equivalent π Representation of Long Transmission Line
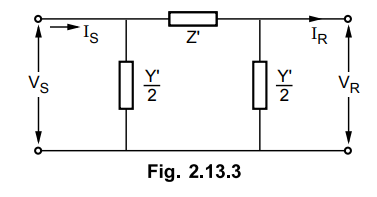
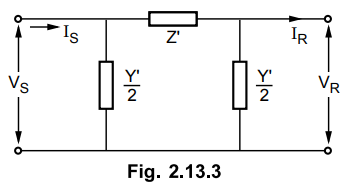
Consider now the following network shown
in Fig. 2.13.3 to determine the equivalent-л network of long transmission line.
From analysis of this network carried
out earlier, we have
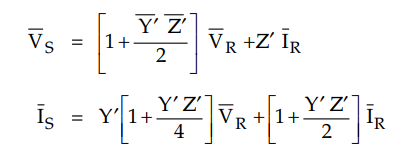
Comparing above equations with those
obtained for long transmission line using rigorous analysis.
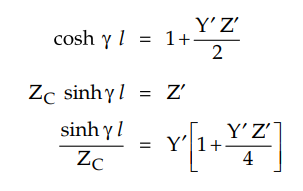
Consider the equation of series branch
impedance,
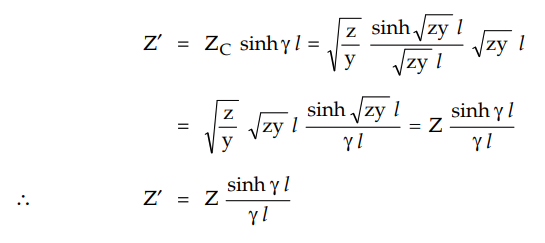
This shows that the series branch
impedance of equivalent n network can be obtained by multiplying series branch
of nominal π (lumped series impedance) by the factor (sinh ɤ l) / ɤ l.
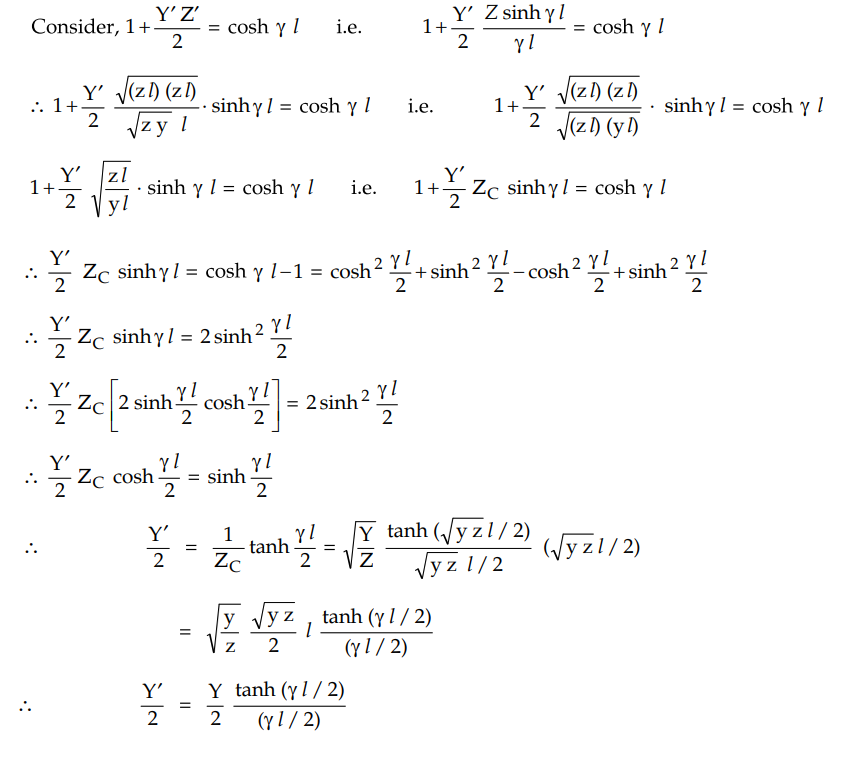
This indicates that the shunt branch of the equivalent л network can be determined by multiplying the shunt branch of the nominal-л (lumped shunt admittance) network by factor tanh (ɤl / 2) (ɤl /2)
The equivalent network is shown in the Fig. 2.13.4.
Review Question
1. Explain Т and л equivalent representation of long transmission line.
Transmission and Distribution: Unit II: (a) Modelling and Performance of Transmission Lines : Tag: : Modelling and Performance of Transmission Lines - Equivalent T and π Network of Long Transmission Line
Related Topics
Related Subjects
Transmission and Distribution
EE3401 TD 4th Semester EEE Dept | 2021 Regulation | 4th Semester EEE Dept 2021 Regulation
