Evaluation of Postfix Expressions

Evaluation of Postfix Expressions

AU: Dec.-15,18, Marks 16

As we have seen how to convert given infix expression to postfix form. It's the time to learn an evaluation of postfix expression. Again use of stack is necessary in postfix expression evaluation. But here we will use the stack for storing operands rather than operators. Operands are taken as numeric values. Let us see an algorithm first,

Algorithm for evaluation of postfix.

1. Read the postfix expression from left to right.

2. If the input symbol read is an operand then push it on to the stack.

3. If the operator is read POP two operands and perform arithmetic operations if operator is

+ then result = operand 1 + operand 2

- then result = operand 1-operand 2

* then result = operand 1 * operand 2

/ then result = operand 1 / operand 2

4. Push the result onto the stack.

5. Repeat steps 1-4 till the postfix expression is not over.

 

Ex. 4.7.1: Evaluate given postfix expression.

ABC-BA + C $ - for A = 1, B = 2 and C = 3

Sol. Now as per the algorithm of postfix expression evaluation, we scan the input from left to right. If operand comes we push them onto the stack and if we read any operator, we must pop two operands and perform the operation using that operator. Here $ is taken as exponential operator.

Now since there is no further input we should pop the contents of stack and print it as a result of evaluation.

Hence output will be - 27.

 

Ex. 4.7.2 : Program for evaluation of postfix expression.

Sol. :

/******************************************************************

Program to evaluate a given postfix expression.

******************************************************************/#include <stdio.h>

#include <conio.h>

#include <stdlib.h>

#include <string.h>

#include <math.h>

#define size 80

/*declaration of stack data structure*/

struct stack

{

double s[size];

int top;

}st;

void main()

{

char exp[size];

int len;

double Result;

double post();

clrscr();

printf("Enter the postfix Expression\n");

scanf("%s", exp);

len = strlen(exp);

exp[len] = '$'; /* Append $ at the end as a endmarker*/

Result = post(exp);

printf("The Value of the expression is %f\n", Result);

getch();

exit(0);

}

double post( char exp[])

{

char ch,*type;

double result, val, op1, op2;

void push(double);

double pop();

int i;

st.top = 0;

i=0;

ch = exp[i];

while (ch != '$' )

{

if (ch >= '0' && ch <= '9')

type="operand";

else if (ch== '+'|| ch == '|| ch == "*'|| ch == '/' || ch == '^')

type="operator";

if(strcmp(type, "operand")==0)/*if the character is operand*/

{

val=ch- 48;

push(val); The characters '0', '1', ... '9' will be converted to their values, so that they will perform arithmatic operation

}

else

if (strcmp(type, "operator")==0)/*if it is operator*/

{

op2 = pop();Popping two operands to perform arithmatic operation

op1 = pop();

switch(ch)

}

case '+' result = op1 + op2;

break;

case '-': result = op1 - op2;

break;

case '*' : result = op1 * op2;

break;

case '/' result = op1 / op2;

break;

case '^': result =pow(op1,op2);

break;

}/* switch */

push(result); Finally result will be pushed onto the stack

}

i++;

ch=exp[i];

} /* while */

result = pop(); /*pop the result*/

return(result);

}

void push(double val)

{

if (st.top+1 >= size)

printf("\nStack is Full\n");

st.top++;

st.s[st.top] = val;

}

double pop()

{

double val;

if(st.top == -1)

printf("\nStack is Empty\n");

val = st.s[st.top];

st.top--;

return(val);

}

Output

Enter the postfix Expression

12+34*+

The Value of the expression is 15.0000

Logic of evaluation of postfix expression [Refer the above program]

Let us take some example of postfix expression and try to evaluate it 123+*

Step 1: Assume the array exp[] contains the input

The $ symbol is used as an end marker. Read from first element of the array if it is operand push it onto the stack.

Step 2: If the operator isv read pop two operands

Again pop two operands and perform the operation.

Step 4:

At this point the stack is empty and the input is read as $. So here stop the evaluation procedure and return the result = 5.

 

Ex. 4.7.3: Write an algorithm to convert a infix expression into an postfix expression. Consider following arithmatic expression in postfix notation: 752 + * 415 -/-

i) Find the value of the expression.

ii) Find the equivalent prefix form of above expression.

Sol. : Algorithm to convert infix expression to postfix - Refer section 4.6.

i) Let, the given postfix expression be -

752 + * 415 -/-

ii) Let 752 + * 415 -/-

Step 1: Read expression from left to right. Go on pushing operands onto the stack. When operator is read, pop two operands and form prefix expression push it onto the stack.

Ex. 4.7.4 : Evaluate the following expression using stack 5 6 2 + * 84/- AU: Dec.-15, Marks 2

Sol. :

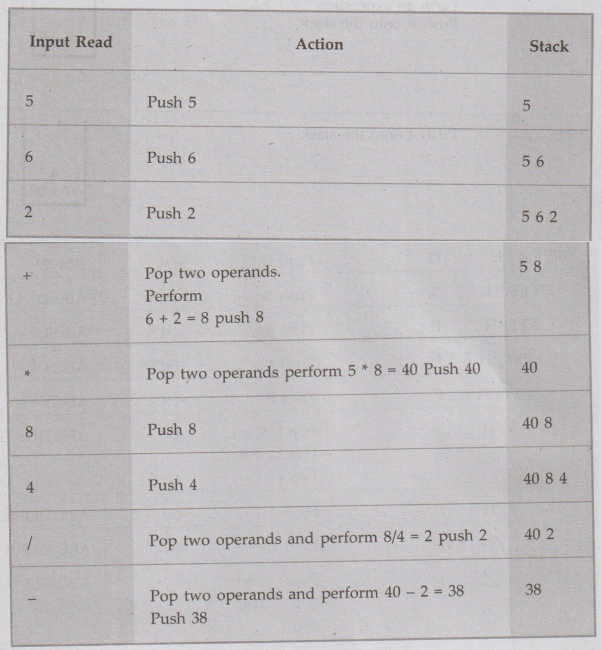
The result of evaluation is 38.

 

Ex. 4.7.5 : Write the procedure to convert the infix expression to postfix expression and the expression steps involved in evaluating the postfix expression. Convert A-(B/C+(D%E*F)/F)*H to postfix form. Evaluate the given postfix expression 9 3 4 * 8 +4 / -

AU: Dec.-18, Marks 7

Sol. : Procedure to convert infix to postfix: Refer section 4.6.

 Conversion of A-(B/C+(D%E*F)/F)*H

Postfix Form : A B C / DE F *% F/ + H * -

The result of evaluation is 4

Review Question

1. Discuss any two applications of stack with relevant examples. AU: Dec.-15, Marks 16