Example Problems Based on Cauchy's Residue Theorem

PROBLEMS BASED ON CAUCHY'S RESIDUE THEOREM

Example 4.3.31. Evaluate using Cauchy's residue theorem,

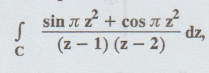
 [A.U. N/D 2011, M/J 2013]

Solution:

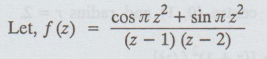
Singular points of the function f (z) are got by equating the denominator to zero, we get

 (z − 1) (z - 2) = 0

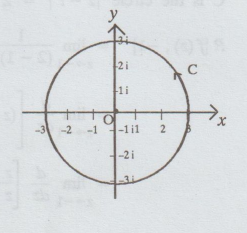
z = 1 lies inside | z |  = 3

z = 2 lies inside | z | = 3

Example 4.3.32. Evaluate 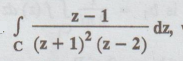 where C is the circle | z - i| = 2 using Cauchy's residue theorem.

 [A.U. M/J 2012]

Solution:

Let f(z) = z – 1 /  (z + 1)² (z - 2)

Singular points of the function f (z) are got by equating the denominator to zero, we get

(z + 1)² (z − 2) = 0

z = -1 is a pole of order 2 lies inside C

z = 2 is a simple pole lies outside C.

C is the circle | z - i | = 2 with centre (0, 1) and radius r = 2.

Example 4.3.33. If C is the circle |z|= 3, then evaluate

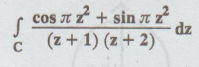
Solution:

Example 4.3.34. Using Cauchy's residue theorem evaluate

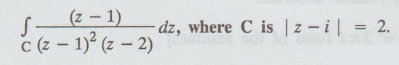
Solution:

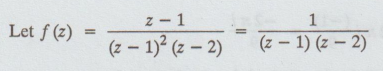
Singular points of the function f (z) are got by equating the denominator to zero, we get (z1) (z - 2) 0.

z = 1 is a simple pole and lies inside C

z = 2 is a simple pole lies outside C

C is the circle |z - i| = 2 with

centre (0, 1) and radius r 2.

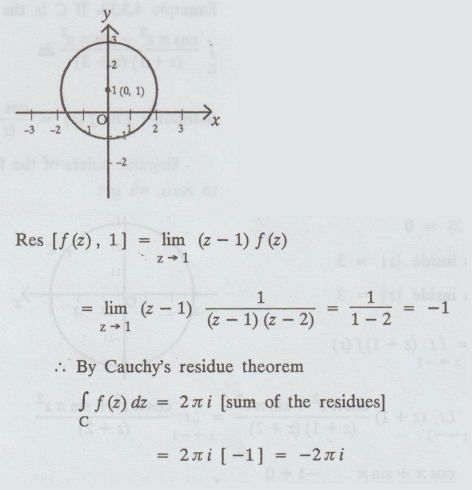
Example 4.3.35. Evaluate 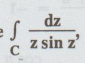where C is |z| = 1 using Cauchy's residue theorem.

Solution: Let f (z) = 1/ z sin z

The singularity of f (z) is given by

z sin z = 0

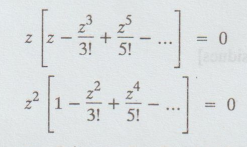
z = 0 is a pole of order 2

z = 0 lies inside C

Example 4.3.36. Evaluate 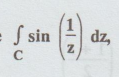 dz, where C is any circle with centre origin.

Solution:

 Let f (z) = sin (1/z)

The only singular point is z = 0 which is inside C.

Sin (1/z) = 1/z – 1/3!z³ + …

Res,[f(z) 0] = co-efficient of 1/z = 1

By Cauchy's residue theorem, we get

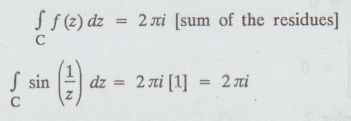
Example 4.3.37. If C is the boundary of the square, whose sides along the lines x = ±2 and y = ±2 and described in the positive sence, find the value

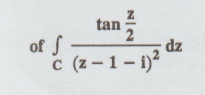
Solution:

Example 4.3.38. Evaluate 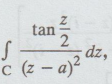 where -2 < a < 2 and C is the boundary of the square whose sides lie along x = ± 2 and y = ±2

Solution:

Example 5.3.39 Evaluate 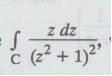 where C is the circle |z - i| = 1, using Cauchy's residue theorem. [A.U N/D 2016 R-13]

Solution:

Let f (z) = z / (z² + 1) ² = z /  [(z + i) (z - i)]²

z = i is a pole of order 2, lies inside |z - i|= 1

z=-i is a pole of order 2, lies outside | z - i | = 1

Given: |z - i| = 1

Here, Centre i, i.e., (0, 1) and radius 1