Probability and complex function: Unit III: Analytic functions

Example Solved Problems based on harmonic conjugate

Next >>

Probability and complex function: Unit III: Analytic functions : Problems based on harmonic conjugate

PROBLEMS BASED ON HARMONIC CONJUGATE

Example 3.2.1. If f (z) = e^z then show that u and v are harmonic functions.

Solution: Given: f(z) = e^z

u + iv = e^{x + iy}= e^x e^iy

= e^x [cos y + i sin y]

= e^x cos y + ie^x sin y

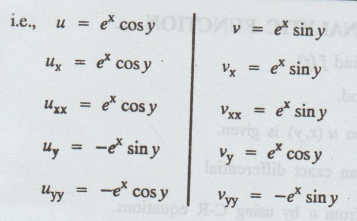
u_xx + u_yy= e^x cos y – ^ex cos y

= 0

v_xx + v_yy = e^x siny - e_x sin y

= 0

Second order partial derivatives of u and v are continuous.

So, u and v are harmonic function.

Example 3.2.2. Give an example such that u and v are harmonic but u + iv is not analytic. [A.U. N/D 2005]

Solution :

Note : u = Re z²

u = x² - y², v = -y/x² + y² v = im 1/z

Example 3.2.3 Find the value of m if u = 2x²- my2+ 3x is harmonic. [A.U N/D 2016 R-13]

Solution: Given: u = 2x² - my² + 3x

∂²u/∂x² + ∂²u/∂y² = 0 [ u is harmonic] .. (1)

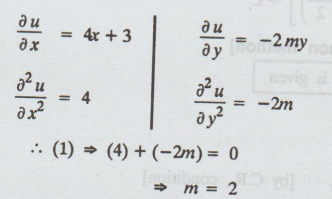
(1) ⇒ (4) + (-2m) = 0

⇒ m = 2

Probability and complex function: Unit III: Analytic functions : Tag: : Analytic functions - Example Solved Problems based on harmonic conjugate

Next >>

Probability and complex function

MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation