Probability and complex function: Unit IV: Complex integration
Exercise : 4.2 (Taylor's and laurent's series)
Problems with Answer | Complex integration
Probability and complex function: Unit IV: Complex integration : Exercise : 4.2
EXERCISE : 4.2
TAYLOR'S AND LAURENT'S SERIES
1.
Expand f (z) = e2z / ( z – 1) about z = 1 using Taylor's series expansion.
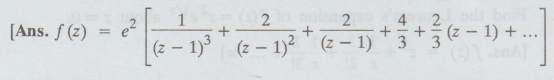
2.
Obtain the expansion of log (1 - z), when | z | < 1 using Taylor's series
expansion.
[Ans. f (z) = -z – z2 / 2 – z3
/ 3 - … ∞ ]
3.
Find the Taylor's series of f (z) = tanh z about the point z = 0.
[Ans. f (z) = z / 1 – z3 / 3 + … ]
4.
Expand the following in Laurent's series :
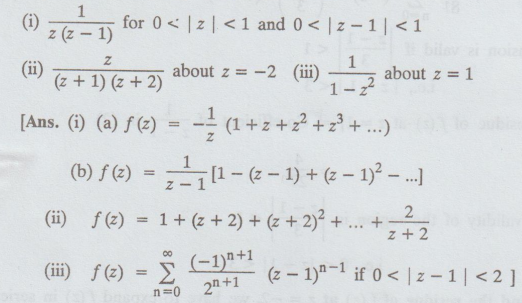
5.
If f (z) = z + 4 / (z + 3) (z - 1)2 find the Laurent's series
expansion in the region.
(i) 0 < | z - 1| < 4 (ii) | z – 1 | >
4
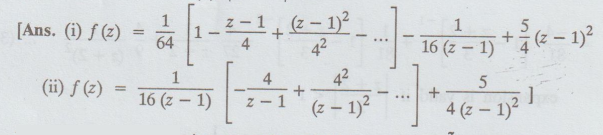
6.
Find the Laurent's series expansion of f (z) = z / (z2 + 1 ) )z2
– 1)2 ]
(i)
1 < z < 2 (ii) | z | > 2
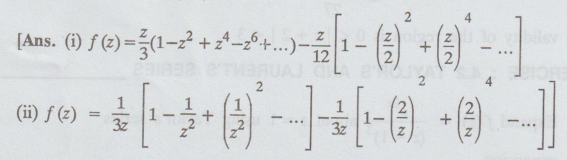
7.
Find the Laurent's expansion of f (z) = 22e1/z about z =
0.
[Ans.
f (z) z2 + 1/z + 1/2! + 1/z 1/3! + ∞]
8.
Obtain the Laurent's Series for f (z) = 1 / (z + 2) (1 + z2) in
(i)
| z | < 1 (ii) 1< | z | < 2 (iii) | z | > 2
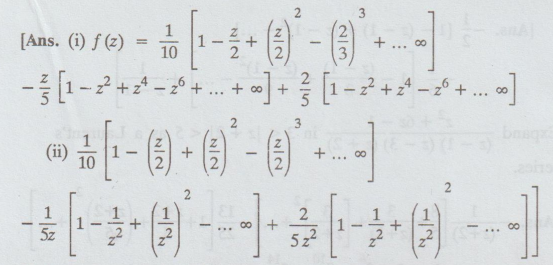
9.
Find the Laurent's series expansion of the function
f(z)
= 1/ z (1 - z)2 and specify the regions in which those expansions
are valid.
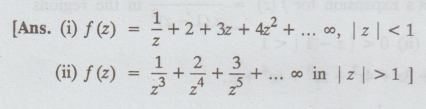
10.
Obtain the Taylor's series for f (z) = 2z3 + 1 / z(z + 1) about z =
i
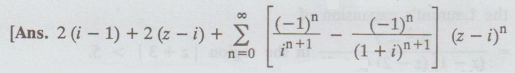
11.
Expand the following functions in Taylor's series
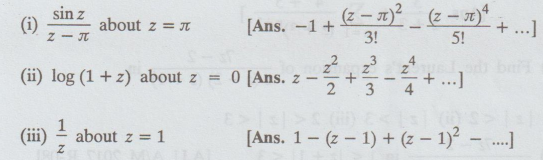
12.
Expand f(z) = z2 / (z + 2) (z − 3) in a Laurent's series expansion
if
(i) | z | < 2 and (ii) 2 < | z | < 3
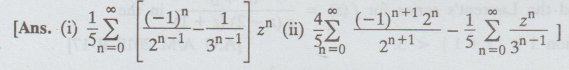
13.
Find first four terms of the Laurent's series expansion valid in the region 0 <|
z - 1| < 1 for the function f(z) = 2z + 1 / z3 + z2 –
2z
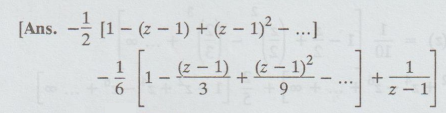
14.
Expand 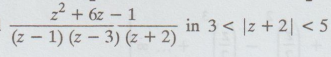 as a Laurent’s series.
as a Laurent’s series.
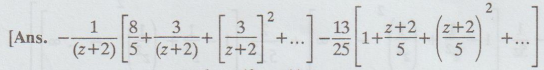
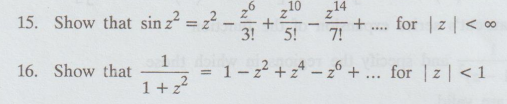
17.
Find the Laurent's expansion for f (z) = 1 / z(1 – z)2 in the regions
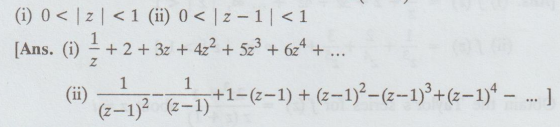
18.
Find the Laurent's expansion of
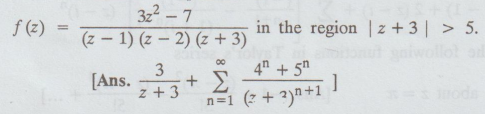
19.
(a) Find the Laurent's expansion of 7z – 2 / z (z+1) (z+2) in
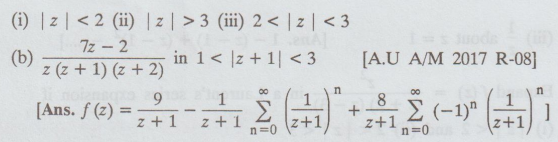
20.
Find the Laurent's series for f (z) = 6z + 5 / z (z − 2) (z+1) in the region 1 < | z + 1 | < 3.
[A.U
A/M 2018 R-17]
21.
Find the Laurent's series for (z - 1) sin 1/z about z = 0
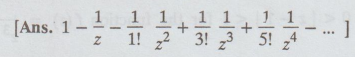
22.
Find the Laurcnt's series for 1 – cos z / z about z = 0
[Ans.
z / 2! – z3 / 4! + z5 / 6! - … ]
23.
Find the Laurent's series for 1/z3 ez2 about z = 0
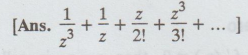
24.
Find the Laurent's series for z-1 e-2z about z = 0
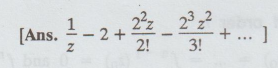
25.
Expand 1 / z2 – 3z + 2 in the region
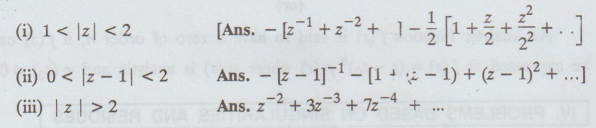
26.
Obtain the expansion of the function f(z) = z – 1 / z2 in Taylor's
series in powers of (z – 1) ) and give the region of validity and Laurent's
series for the domain |z - 1| > 1 [Anna, May 1997]
27.
Expand f (z) = 1 / z (1-z) as a Laurent
series
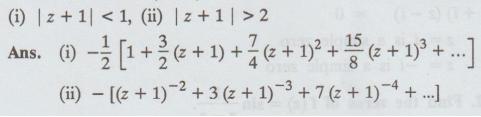
28.
Find the Laurent series expansion of ƒ (z) = 1 / z2 + 4z + 3 valid
in the regions | z | < 1 and 0 < z + 1| < 2 [A.U A/M 2017 R-13]
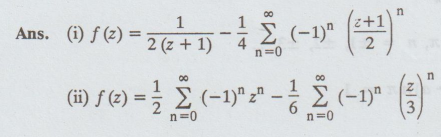
Probability and complex function: Unit IV: Complex integration : Tag: : Problems with Answer | Complex integration - Exercise : 4.2 (Taylor's and laurent's series)
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
