Probability and complex function: Unit I: Probability and random variables
Exercise 1.11 (Exponential distribution)
Problems with Answer | Random variables
Probability and complex function: Unit I: Probability and random variables : Exercise 1.11
EXERCISE 1.11
1.
The time in hours required to repair a machine is exponentially distributed with
parameter λ = 1/2, (i) what is the probability that the repair time exceeds 2
hours? (ii) What is the conditional probability that a repair takes atleast 10
hours given that its duration exceeds 9 hours ?
[Ans.
(i) 0.3679, (ii) 0.6065]
2.
A continuous r.v. X has the p.d.f.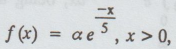 
find ɑ, E [X] and var(X).
[Ans.
α = 1/5, E[X] = 5, var(X) = 25]
3.
The mileage which a car owner gets with a certain kind of tyre is a r.v having
an exponential distribution with mean 40,000 kms. Find the probabilities that
one of these tyres will last (i) atleast 20,000 kms (ii) atmost 30,000 kms.
[Ans.
(i) 0.6065, (ii) 0.5270]
4.
If the continuous r.v. X exponentially distributed with parameter λ find the
pdf of Y = x2.
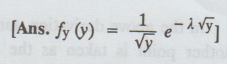
5.
If the p.d.f of the r.v. X is f (x) = e-x , x > 0 find the pdf of
Y = x3
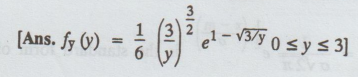
Probability and complex function: Unit I: Probability and random variables : Tag: : Problems with Answer | Random variables - Exercise 1.11 (Exponential distribution)
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation