Exercise 1.12 (Normal distributions)

EXERCISE 1.12

1. If e^{3t + 8t2} is the moment generating function of a normal random variable X, find P [-1 < x < 9].

2. If f (x) = ke^{-(9x2 - 12x + 13)} is the density function of a normal  distribution, k being a constant, find the mean and standard deviation of the distribution.

 [Ans. Mean = 2/3; standard deviation = 1/3 √2]

3. If X is normally distributed with mean zero and variance unity, what is the expectation and variance of e^ax?

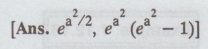
4. The quartiles of a normal distribution are 8 and 14 respectively. Estimate the mean and standard deviation.

[Ans. m = 11, σ = 4.4]

5. Given that X is distributed normally.

P (X ≤ 45] = 0.31 and P [X ≥ 64]  = 0.08, find the mean and standard deviation of the distribution.

 [Ans. m = 50, σ² = 100]

6. In a sample of 1000 cases, the mean of a certain test is 14 and standard deviation is 2.5. Assuming the distribution to be normal find (i) How many students score between 12 and 15 ? (ii) How many score above 18? (iii) How many score below 18? (iv) How many score 16 ?

 [Ans. (i) 443, (ii) 54, (iii) 8, (iv) 116]

7. The average test marks in a particular class is 79. The S.D is 5. If the marks are distributed normally, how many students in a class of 200 did not receive marks between 75 and 82?

 [Ans. 97]

8. In a sample of 120 workers in a factory the mean and standard deviation of wages were Rs. 11.35 and Rs. 3.03 respectively. Find the percentage of workers getting wages between Rs. 9 and Rs. 17 in the whole factory nodW (in) assuming that the wages are normally distributed?

[Ans. 75.09%]

9. At a certain examination 10% of the students who appeared for the paper in statistics got less than 30 marks and 97% of the students got less than 62 marks. Assuming the distribution is normal, find the mean and the S.D. of the distribution.

 [Ans. μ = 43.04, σ = 10.03]