Exercise 1.2 and Exercise 1.3 (Conditional Probability, Baye's Theorem)

EXERCISE 1.2 and EXERCISE 1.3

1. Prove that if P(A) > P(B) then P(A/B) > P(B/A)

2. From 5 red balls and 8 white balls, 4 balls are chosen at random (without replacement) find the probability that they are of the red colour.

 [Ans. 1/143]

3. A card is drawn from a well shuffled pack of 52 cards. What is the W probability that it is either clever or king.

[Ans. 4/13]

4. A box contains 4 bad and 6 good tubes. Two are drawn out together. One of them is tested and found to be good. What is the probability that the other one is also good.

 [Ans. 5/9]

5. It is 8 5 against a person who is now 40 years old living till he is 70 and 4.3 against a person now 50 living till he is 70. Find the probability that atleast one of these persons will be alive 30 years.

[Ans. 1 – 8/ 13 × 4/7 = 59 / 91 = 0.64835]

6. Given P(A) = 0.50, P(B) = 0.30 and P(A ∩  B) = 0.15,

Verify that (a) P (A/B) = P(A)

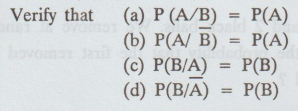
7. A certain item is manufactured by three factories say 1, 2 and 3. It is known that 1 turn out twice as many item as 2 and that 2 and 3 turns out the same number of item (during a specified production period). It is also known that 2 percent of the items produced by 1 and 2 are defective, while 4 percent of those manufactured by 3 are defective. All the items produced are but into one stockpile, and then one item is chosen at random. What is the probability that this item is defective ?

[Ans. 0.025]

8. A box contains five balls. The balls are drawn and found to be white. What is the probability that all the balls being white.

[Ans. 1]

9. Two students A and B work independently on a problem. The probability that the first one will solve it is 3/4 and the probability that the second one will solve it is 2/3 What is the probability that the problem will be solved ?

[Ans. 11/12]

10. An urn contains 5 white and 3 green balls and another urn contains 3 white and 7 green balls. Two balls are chosen at random from the first urn and put into the second urn, Then a ball is drawn from the second urn, what is the probability that it is a white ball?

[Ans. 0.372]

11. Ten chips numbered 1 to 10 are mixed in a bowl. Two chips are drawn from the bowl successively and without replacement. What is the probability that their sum is 10?

[Ans. 4/45]

12. A bag contains 10 tickets numbered 1, 2, ... 10. Three tickets are drawn at random are arranged in ascending order of magnitude. What is the probability, that the middle number is 5?

 [Ans. 1/6]

13. Four persons are chosen at random from a group consisting of 4 men, [283 women, and 2 children. Find the chance that the selected group contains at least one child.

 [Ans. 13/18]

14. A box contains 3 white balls and 2 black balls. We remove at random 2 balls in succession, what is the probability that the first removed ball is white and the second is red ?

6 / 25 (if the ball is replaced),

3/10 (if the ball is not replaced)

15. An urn contai.s ten white and three black balls. Another urn contains three white and five black balls. Two balls are drawn at random from dos the first urn and placed in the second urn and then one ball is taken at random from the latter. What is the probability that it is a white ball?

 [Ans. 59/120]

16. Urn I has two white and three black balls. Urn II has four white and one black balls and urn III has three white and four black balls. An urn is selected at random and a ball drawn at random is found to be white. Find the probability that urn I was selected.

[Ans. 14/57]

17. A bag contains seven red and three black marbles and another bag contains four red and five black marbles. One marble is transferred from the first bag into the second bag and then a marble is taken out of the second bag at random. If this marble happens to be red, find the de probability that a black marble was transferred.

[Ans. 12/47]

18. There are three true coins and one false coin with head on both sides. A coin is chosen at random and tossed four times. If head occurs all soib the four times, what is the probability that the false coin has been chosen and used ?

[Ans. 16/19]

19. Three urn contains three white, one red and one black balls; two white, three red and four black balls; one white, three red and two black balls respectively. One urn is chosen at random and from it two balls are drawn at random. If they are found to be one red and one black balls, W what is the probability that the first urn was chosen ?

[Ans. 3/25]

20. A bolt is manufacatured by three machines A, B, C. A turns out twice as many items as B and machines B and C produce equal number of items. Two percent of bolts produced by A and B are defective and four percent of bolts produced by C are defective. All bolts are put into one stock pile and one is chosen from this pile. What is the probability that it is defective.

[Ans. 1/40]