Exercise 1.8 (Poisson distribution)

EXERCISE 1.8

1. A large shipment of text books contains 2% with imperfect bindings. What is the probability that among 400 text books, taken from this shipment exactly 5 have imperfect bindings? 

[Ans. 0.09]

2. The probability of getting no misprint in a page of a book is e^-4. What is the probability that a page contains (a) 2 misprints (b) more than 3 misprints? 

[Ans. (a) 0.1465 (b) 0.5665]

3. In a certain factory producing cycle tyres, there is a small chance of 1 in 500 tyres to be defective. The tyres are supplied in lots of 10. Using Poisson distribution calculate the approximate number of lots containing no defective, one defective and two defective tyres respectively, in a consignment of 10,000 lots. 

[Ans. (i) 9802 lots (ii) 196 lots (iii) 2 lots]

4. Using Poisson distribution, find the probability that the ace of spades will be drawn from a pack of well shuffled cards atleast once in 104 consecutive trails.

[Ans. 0865]

5. Out of 1000 balls, 50 are red and the rest white. If 60 balls are picked at random, what is the probability of picking up (i) 3 red balls (ii) not more than 3 red balls in the sample? 

[Ans. (i) 0.2241 (ii) 0.6474]

6. Find the probability that atmost 5 defective fuses will be found in a box of 200 fuses if experience shows that 2% of such fuses are defective. 

[Ans. 0.785]

7. It is known from past experience that in a certain plant there are on the Jers. average 4 industrial accidents per month. Find the probability that in a given year there will be less than 4 accidents. 

[Ans. 0.4332]

8. A distributor of bean seeds determines from extensive tests that 5% of large batch of seeds will not germinate. He sells the seeds in packets of > 200 and guarantees 90% germination. Determine the probability that a Isupo particular packet will violate the guarantee. 

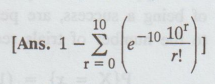
9. An automatic machine makes paper clips from coils of a wire. On the bas aver average, 1 in 400 paper clips is defective. If the paper clips are packed in boxes of 100, what is the probability that any given box of clips will bomu contain (i) no defective, (ii) one or more defectives, (iii) less than two defectives. 

[Ans. (i) 0.7787, (ii) 0.2213, (iii) 0.97344]

10. x is a Poisson variate with λ = 1.5 Find the probability that (i) x = 3 (ii) x ≤ 3; 

[Ans. 0.125; 0.934]

11. If 2.5% of the units produced in a factory are known to be defective, find the probability that in a box of 100 units produced by the factory 3 or less are defective. 

[Ans. 0.758]

12. If one in a thousand workers in a factory has a lung disease find the olgo probability that among 2000 workers 2 or 3 will have that disease. 

[Ans. 0.451]

13. In a company, on an average 3 workers are absent. Assuming Poisson distribution find the probability that 5 are absent on a particular day. 

[Ans. 0.101]

14. 1% of the units manufactured by a company are defective. They are bodo packed in boxes of 250 each. Find the probability that a particular box Jon (contains 4 defectives. In one thousand such boxes how many boxes may be expected to contain less than 2 defectives? 

[Ans. 0.134; 287]

15. The probability that a man aged 50 will die within the next year is 0.002. What is the probability that out of 100 such persons 98 will survive till evrbolab our aut nous to next year? 

[Ans. 0.984]

16. It is known that on an average 1 triplet is born in 10,000 births. What is the probability of three triplets in a city in which there are 25,000 novig births in a year? 

[Ans. 0.214]