Exercise

EXERCISE

1. A circuit has 1000 turns enclosing a magnetic circuit 20 m2 in section. With 4A the flux density is 1 wb/m² and with 9A it is 1.4 wb / m². Find the mean value of the inductance between these current limits and the induced electromotive force if the current fell uniformly from 9A to 4A in 0.05 sec.

[Ans: 0.16 H, 16 V]

2. The total inductance of two coils, A and B, when connected in series is 0.5H or 0.2H depending on the relative directions of the current in the coils. Coil A, when isolated from coil B, has a self-inductance of 0.2H. Calculate (a) the mutual inductance between the two coils, (b) the self-inductance of coil B, (c) the coupling factor between the coils. (d) the two possible values of the induced e.m.f. in coil A. The current is decreasing at 1000A per second in the series circuit.

[Ans: 0.075H; 0.15H; 0.433; 275 volts; 125 volts]

3. Obtain the equivalent inductance of the parallel connection of L1 and L2 shown in the fig. 5.42.

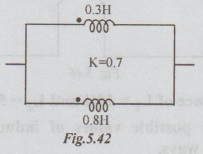
 [Ans: 0.296 H]

4. Determine the value of K in the coupled circuit of the figure 5.43, if the power in the 10 ohm resistor is 32 watts.

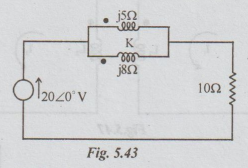
 [Ans : 0.791]

5. For the circuit shown in fig. 5.44, find the ratio of output voltage to the input voltage.

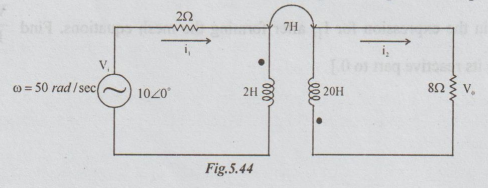
6. Find the equivalent impedance of the coupled circuit shown in fig. 5.45.

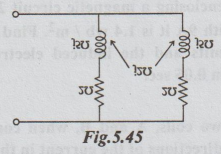
[Ans: 1 + j 1.50Ω]

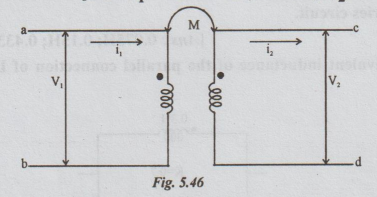
7. In fig5.46, L₁ = 2H; L₂ = 6H; K = 0.5; i₁ = 4 sin (40 t-30°) A; i₂ = 2 sin (401-30°) A. Find the values of (i) v₁ and (ii) v₂.

 [Ans: v₁ = 181.44 cos (40t-30°), v₂ = 202.88 cos (40t-30°)]]

8. Two coils have self inductance of L1 = 10H and L2 = 5H. The mutual inductance between them is 3H. Find all the possible values of inductance which can be obtained by connecting them in various ways.

[Ans: Series: 21 or 9; parallel: 2.28, 3.5; short circuited: 8.2 or 4.1 H]

9. Find the value of C in fig. 5.47, given that the supply voltage and current are in phase.

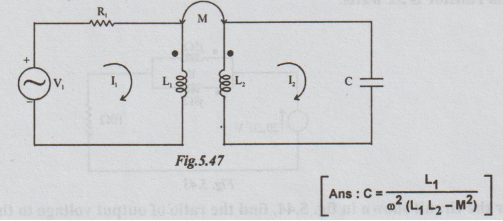
 [Hint: Obtain the expression for I1, after forming the mesh equations. Find in rectangular form. Equate its reactive part to 0.]