Exercise 2.1 (Discrete and Continuous Random Variable)

EXERCISE 2.1

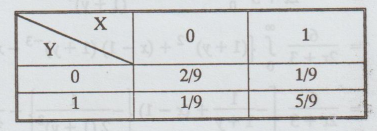
1. Two discrete random variables X and Y have P(X = 0,Y = 0) = 2 / 9.

P(X = 1, Y = 1) = 5/9. Examine whether X and Y are independent.

Hint : 

2. The density function of a two dimensional continuous random variables is given as

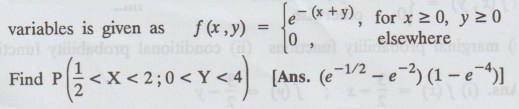
3. Two r.v.'s X and Y have the joint p.d.f.

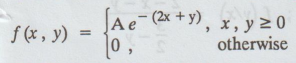
(i) Find (A) (ii) Find the marginal pdf (iii) Find the joint c.d.f.

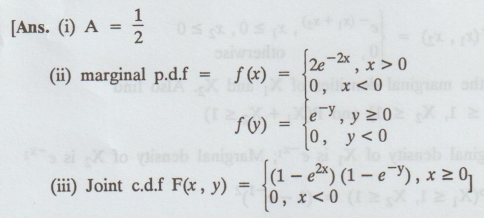
4. Consider the two-dimensional density function

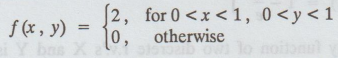
 (i) Find the marginal density function.

(ii) Find the conditional density function.

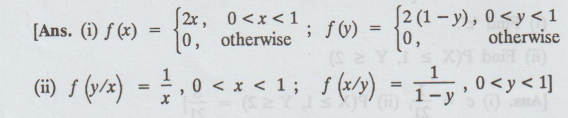
5. Verify whether X and Y are statistically independent or not given

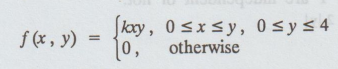
[Ans. X and Y are not independent ]

6. If X and Y have the j.p.d.f

Find (i) P(0 < x < 1/y = 2) (ii) P(X > Y) (iii) P(X + Y < 1)

 [Ans. (i) 1 –  1/e, (ii) 1/2, (iii) 1–2/e]

7. If f (x, y) = 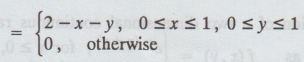 find

(i) marginal probability functions (ii) conditional probability functions

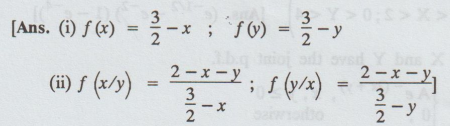
8. Let X₁ and X₂ be two r.v.'s with joint density function given by

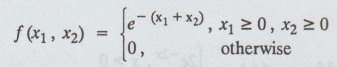
Find the marginal densities of X₁ and X₂. Also find

P(X₁ ≤ 1, X₂ ≤ 1) and P(X₁ + X₂ ≤ 1)

[Ans. Marginal density of X₁ is e^-x1; Marginal density of X₂ is e^-x2

P(X₁ ≤ 1, X₂ ≤ 1) = (1 - e^-1)²

P(X₁ + X₂ ≤ 1) = 1- 2/e]

9. The joint probability function of two discrete r.v.'s X and Y is given by

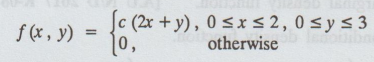
 (i) Find 'c'.

 (ii) Find P(X = ≥ 1, Y ≤ 2)

[Ans. (i) c = 1/21, (ii) P(X ≥ 1, Y ≤ 2) = 8/21]

10. Test whether X and Y are independent or not.

f(x, y) = Ae^{- | x | -2 | y} |

[Ans. independent]

11. The joint probability density of the r.v.'s X and Y is

f(x, y) = 1/4  e ^{- |x| - |y|} , - ∞ < x < ∞, ∞ < y < ∞.

(a) Are X and Y statistically independent variables.

(b) Calculate the probability that X ≤ 1 and Y ≤ 0.

[Ans. (a) Independent ; (b) P(X ≤ 1, Y ≤ 0) = (2 - e ^-1)]

12. If X and Y are two random variables, having joint density function

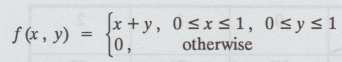
Determine the marginal distribution of x and y.

 [Ans. f (x) = (x + 1/2), 0 ≤ x < 1 ; f(y) = y + 1/2, 0 ≤ y ≤ 1]

13. The Joint probability density function of the two random variables X and Y is given by

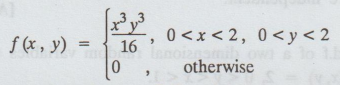
Find the marginal density of X and Y.

14. The random variables X and Y have the j.p.d.f

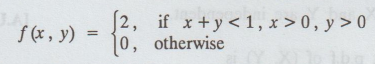
Find the conditional distribution of Y given X = x.

15. Two random variables have the j.p.d.f given by

Show that X and Y are independent.

16. Let X and Y be two random variables with j.p.d.f

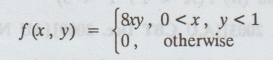
Find (i) the joint distribution function of X and Y, (ii) the marginal probability density of Y.

17. Let X and Y be jointly distributed with p.d.f.

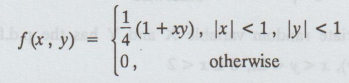
Show that X and Y are independent.

18. If f (x, y) = 1 / 2x² y for 1 ≤ x < ∞ and 1/x < y < x is the j.p.d.f of the random variables X and Y, find

(i) marginal distributions of X and Y.

(ii) the conditional distribution of Y given X = x.

19. The joint probability mass function (p.m.f) of X and Y is

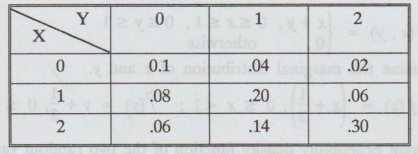
Compute the marginal p.m.f X and of Y, P [X ≤ 1, Y≤ 1] and check if X and Y are independent. [A.U N/D. 2004]

20. If the joint p.d.f of a two dimensional random variables (X, Y) is given by f(x, y) = 2, 0 < y < x < 1.

= 0, otherwise

Find the marginal density function of X and Y.

Also find X and Y are independent. [A.U. A/M. 2003]

21. If the joint p.d.f of (X, Y) is

f(x, y) = 1/4 , 0 ≤ x, y ≤ 2, find P (X + Y ≤ 1).

22. If the joint p.d.f of a two dimensional random variables (X, Y) is given by

f(x, y) = K (6-x-y), 0 < x < 2,2 < y < 4

= 0, otherwise

Find (i) the value K (ii) P(X < 1, Y < 3); (iii) P(X + Y < 3) and (iv) P(X < 1 / Y < 3)

[A.U. 2003] [A.U CBT Dec. 2009] [AU N/D 2009]

23. Find 'k' if the joint probability density function of a bivariate random variable (X, Y) is given by

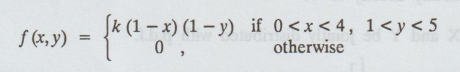
24. Find k if the bivariate random variable X and Y has the p.d.f

ƒ (x, y) = k x² (8 − y), x < y < 2x, 0 ≤ x < 2

25. If X and Y have joint p.d.f.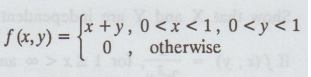

Check whether X and Y are independent.

26. Find the marginal density functions of X and Y, if

f(x, y) = 2/5 (2x+5y), 0 < x < 1, 0 < y < 1

27. The joint p.d.f of the two dimensional random variable is

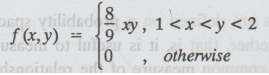
(i) Find the marginal density functions of X and Y.

(ii) Find the conditional density function of Y given X = x

28. The joint p.d.f of X and Y is given by

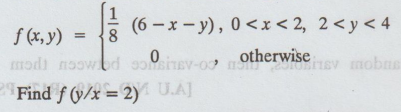
29. The joint p.d.f of a two dimensional random variable (X, Y) is  given by f (x, y) = xy2 + x2/8, 0 ≤ x ≤ 2, 0 ≤ y ≤ 1. Compute

(i) P (X > 1/Y < 1/2)

(ii) P [ Y < 1/2 / X > 1]

(iii) P [X < Y]

 (iv) P(X + Y ≤ 1]

30. The joint p.d.f of a bivariate R.V (X, Y) is given by

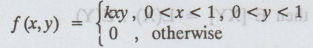
(i) Find k

(ii) Find  P (X + Y < 1)

(iii) Are X and Y independent random variables

31. Let X and Y be two random variables with the joint p.d.f

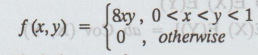
 (i) Find the marginal p.d.f of X and YX)

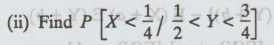
(iii) Check X and Y are independent

(iv) Find E [X] and E [Y]