Exercise 2.3 (Regression)

Exercise 2.3

1. In a partially destroyed laboratory record, only the lines of regression of x and x on y are available as 4x-5y+33 20x9y= 107 respectively, calculate x, y and the coefficient of correlation between x and y.

Ans. r = ± 3/5

2. The following table gives the data on rainfall (x inches) and discharge in a certain river (y units). Obtain the line of regression of y on x. Estimate from it, the discharge corresponding to a rainfall of 2 inches.

3. The following are results pertaining to heights (x) and weights (y) of 1000 industrial workers.

Estimate the following

 (i) The weight of a particular worker who is 5 feet tall

(ii) The height of a particular worker whose weight is 200 lbs

Ans. (i) 111.6 (ii) 71.75

4. Find the regression lines and Karl Pearson's co-efficient of correlation o from the following table.

5. The regression equations of two variables x and y are x = 0.7y + 5.2 and y = 0.3x+2.8. Find the means of the variables and the co-efficient of correlation between them.

Ans. r = 0.458

6. The two regression lines are 3x+2y= 26 and 6x + 3y = 31. Find the correlation co-efficient.

Ans. r = -0.866

7. Given that 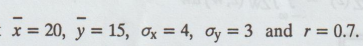. Find the two regression equations and find the value of y when x = 24.

Ans. y = 17.1

8. The coefficient of correlation between two variables x and y is 0.8 and the regression co-efficient of y on x is 1.6. 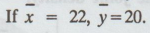. Find the regression co-efficient of x on y and the two regression equations.

Ans. Regression equation of x on y: x = 0.4y + 14,

Regression equation of y on x: y = 1.6x-15.2

9. If the equations of the two lines of regression of y on x and x on y are respectively, 7x - 16y + 9 = 0; 5y - 4x-3 = 0, calculate the co-efficient of correlation,[AU, May, '99]