Exercise 2.4 (Transformation of random variables)

EXERCISE 2.4

1. Let f_x (x) = 2x, 0 ≤ x ≤ 1 and f_y (y) = y²/9, 0 ≤ y ≤ 3 be the p.d.f of the 2 independent random variables. Find the p.d.f of XY.

2. If X and Y are independent random variables with identical uniform distributions in the interval (-1, 1), find the density function' of Z = X + Y.

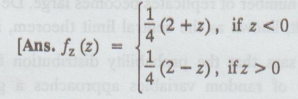
3. If X and Y are independent Random variables with

fX^(x) = e^-x, fY(y) = 3e^-3y find fz (z), if Z = X / Y

4. If X and Y are independent random variables with identical Suniform distributions in (0, 1), find (i) the joint density function eqler of (U, V), where U= X + Y and V = X - Y;

(ii) the density function of U and (iii) the density function of V.

5. If X₁ and X₂ are independent uniform variates on [0, 1], find Svicthe distribution of X₂₁/X₂ and X₁ X₂.

6. Let X be a continuous random variable with

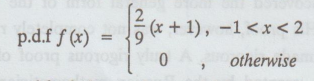
Find the p.d.f of the random variable Y = X²  [AU M/J 2006]

7. The joint p.d.f of the two dimensional random variable is

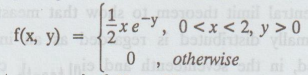
Find the p.d.f of X + Y.   [A.U N/D 2016 R13 (RP)]

8.  (i) Write down the formula to find the p.d.f of Z = XY in terms of p.d.f of X and Y if they are independent.

 (ii) If U = X + Y and V=X - Y how are the joint p.d.f of (X, Y) and (U, V) related.

9. If the joint p.d.f of X1 and X2 is given by

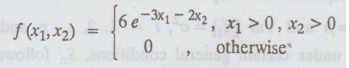
the probability density of U = X₁ + X₂