Exercise 2.5 (Central limit theorem)

EXERCISE 2.5

1. The guaranteed average life of a certain type of electric light bulb is 1000 h with a S.D. of 125 h. It is decided to sample the output so as to ensure that 90% of the bulbs do not fall short of the guarnteed average by more that 2.5%. Use CLT to find the minimum sample size ?

2. If X_i, i = 1, 2… 50 are independent RVs, each having a poisson distribution with parameter λ = 0.03 and S_n = X₁ + X₂ + ... X_n find P (S_n ≥ 3) using CLT. Compare your answer with the exact value of the probability.

3. A random sample of size 100 is taken from a population whose mean is 60 and variance is 400. Using CLT with what probability can we assert that the mean of the sample will not differ from μ = 60 by more than 4?

4. Test whether the CLT holds good for the sequence {X_k} if

P {X_k = ±2^k} = 2^-(2k+1), P (X_k = 0) = 1 - 2^-2k

5. The lifetime of a special type of battery is a random variable with mean 40 hours and standard deviation 20 hours. A battery is used until it fails, at which point it is replaced by a new one. Assuming a stockpile of 25 such batteries the lifetimes of which are independent, approximate the probability that over 1000 hours of use can be obtained.

[Ans. 0.1587]

6. Let X₁, X₂, ... X₁₀ be independent Poisson random variable with Mean 1. Use the Central limit theorem to approximate

P {X₁ + X₂ + ... + X₁₀ ≥ 15}.

7. Let X_k, i = 1, 2, ... 10 be independent random variables, each being uniformly distributed over (0, 1). Calculate

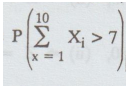
 [Ans. 0.01391]

8. Let X be the number of times that a fair coin flipped 40 times, lands heads. Find the probability that X = 20.

[Ans. 0.1272]

9. The guaranteed average life of a certain type of electric light bulb is 1000 h with a standard deviation of 125 h. It is decided to sample the output so as to ensure that 90% of the bulbs do not fall short of the guaranteed average by more than 2.5%. Use Central limit theorem to find the minimum sample size.

 [Ans. 41]