Exercise 3.1 (Analytic function necessary conditions - Cauchy - Riemann equations)

EXERCISE 3.1

I. Examine the following functions are analytic or not

1. f(z) = e^x (cos y + i sin y)

[Ans. analytic]

2. f(z) = e^x (cos y - i sin y)

[Ans. not analytic]

3. f(z) = z³ + z

[Ans. analytic]

4. f (z) = sin x coshy + i cos x sinh y

[Ans. analytic]

5. f(z) = (x² – y² + 2xy) + i (x² – y² -2xy)

 [Ans. not analytic]

6. f(z) = 2xy + i (x² - y²)

 [Ans. not analytic]

7. f(z) = cosh z

[Ans. analytic]

8. f(z) = y

[Ans. not analytic]

9. f(z) = (x² - y² - 2xy) + i (x² - y² + 2xy)

[Ans. analytic]

10. f(z) = x – iy / 2y²

[Ans. not analytic]

11. f(z) = x – iy / x² + y²

[Ans. analytic]

II. For what values of z, the function ceases to be analytic.

1.  1 / z² – 1

 [Ans. z = ± 1]

2. z² – 4 / z² + 1

[Ans. z = ± i]

3. z³ - 4z -1

 [Ans. for all z, f (z) is analytic]

III. Verify C-R equations for the following functions.

1. f(z) = ze^-z

2. f(z) = ɑz + b

3. f(z) = sin z

IV. Prove that the following functions are nowhere differentiable.

1. f(z) = Re (z) = x

2. f(z) = e^x (cosy - i sin y)

3. f(z) = Im(z) = y

4. f(z) = | z |

5. f(z) = z – 

V. Find the constants a, b, c so that the following are differentiable at every points

1. f(z) = x + ɑy - i (bx + cy)

[Ans. a = b, c = -1]

2. f(z) = ɑx² - by² + i cxy

[Ans. a = b = c / 2]

VI. Prove that f(z) =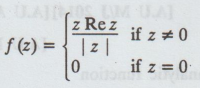

is continuous at z = 0, but not differentiable at z = 0.

VII. Prove that ƒ (z) = xy (y – ix) / x² + y² , when z ≠ 0 and ƒ (0) = 0 is continuous at the origin.

VIII. If w is an analytic function of z, prove that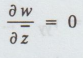 

IX. Prove that the function f(z) = u + iv where

f(z) = x³(1 + i) − y³ (1 − i ) / x² + y² for z ≠ 0 and ƒ (0) = 0

is continuous and the C-R equations are satisfied at the origin.

Is f (z) analytic at the origin?