Exercise 3.3 (Construction of Analytic functions)

EXERCISE

Construction of an analytic function

1. Show that the function u (x, y) = 3x²y + 2x³ – y³ – 2y² is harmonic function. Find the conjugate and analytic function of v and express u + iv is an analytic functin of z. 

[Ans. v (x, y) = 3x²y + 4xy - x³ + C, f(z)= -iz³ +2z² + iC where C is a real constant ]

2. Prove that the function v = sin x coshy + 2 cos x sinh y + x² - y² + 4xy satisfies Laplace's equation. Determine the corresponding analytic function. 

[Ans. f (z) = (2 + i) (z² + sin z) + C]

3. If f (z) = u + iv is an analytic function of z, and if u = 2 sin 2x / e^2y + e^-2y - 2 cos 2x find c. 

[Ans. v = -2 sinh 2y / e^2y + e^-2y - 2 cos 2x + C]

4. Find v such that wu+iv is an analytic function of z, given that u = 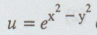 cos 2 xy. Hence find w.

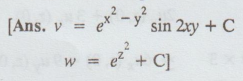
5. Find the analytic function w = u + iv if v = e^2x (x cos 2y - y sin 2y). Hence find u. [A.U A/M 2015 R13] 

[Ans. w = ize2z + C , u = - (x sin 2y + y cos 2y) e^2x + C]

6. Find a harmonic conjugate of u = x⁴ - 6x² y² + y⁴ 

[Ans. v = 4yx³ - 4xy³ + C]

7. find u = x – y /x² + y² such that u + iv is an analytic function. What is the harmonic conjugate of v? 

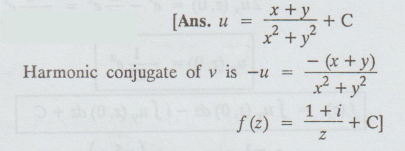
8. Find the analytic function whose real part is sin 2x /cosh 2y + cos 2x

 [Ans. f (z) = tan z + C] [A.U N/D 2019 (R17)]

9. Find the analytic function whose imaginary part is -e^-2xy cos (x² - y²)

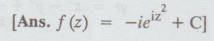
10. Prove that u = 2x - x³ + 3xy² is harmonic and find its harmonic conjugate. Also find the corresponding analytic function.  

[Ans. v = 2y - 3x²y + y³ + C, f(z) = 2z -z³ + ic]

11. Show that u (x, y) = sin x cosh y + 2 cos x sinh y + x² - y² + 4xy is harmonic. Find an analytic function f (z) interms of z with the given u for its real part.  

[Ans. f (z) = sinz + z² - 2i sinz - 2iz² + C]

12. Given v (x, y) =x⁴ - 6x² y² + y⁴, find f (z) = u(x, y) + iv (x, y). Show that f(z) is analytic. 

[Ans. f (z) = iz⁴ + C]

13. If u + v = (x − y) (x² + 4xy + y²) and f (z) = u + iv find the analytic function f (z) interms of z. 

[Ans. z3 + C]

14. Find the real part of the analytic function whose imaginary part is e^-x [xy cos y + (y² - x²) sin y]. Construct the analytic function. 

[Ans. u = e^-x[(x² - y²) cos y + 2xy sin y  f(z)=  z²e^-z + C ]

15. If u (x, y) is a harmonic function in a region D, prove that f(z) = ∂u/∂x - ∂u/∂y is analytic in D.

16. Show that the following functions are harmonic and find a corresponding analytic function f (z) = u + iv. Also find its harmonic conjugate.

(i) u = e^x cos y. [Ans. f(z) = e^z + C, v = e^x sin y]

(ii) u = x / x² + y²  [Ans. f (z) == 1/z + C, v = -y/x² + y² + C]

 (iii) v = -sin x sinh y [Ans. f (z) = cos z + C, u = cos x cosh y + C]

17.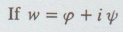 represents the complex potential for an electric field and ψ = 3x²y - y³, find the potential function .

[Ans.  =x³ - 3x² + c]

18. An incompressible fluid flowing over the xy plane has the velocity potential

 = x² - y² + x /x² + y²

Examine if this is possible and find a stream function ψ

[Ans. ψ = 2xy – y/x² + y² +C]

19. Determine the analytic function f(z) = u + iv if u – v = cos x + sin x – e^-y/2 (cosx- coshy) given that f(π/2) = 0 

[Ans. f (z) = ½ [ 1- cot(z/2)]]

20. Find the analytic function f (z) = u + iv given that that 2u + v = e^2x [(2x + y) cos 2y + (x - 2y) sin 2y] 

[Ans. f (z) = ze^2z + C]

21. Prove that u = x² – y² , v = -y/x² + y² bth satisfy the Laplace equation but u + iv is not analytic. [A.U N/D 2015 R-13]

22. Is there an analytic function f (z) = u + iv for which v = e^y/x ? [^Ans. v cannot be the imaginary part of an analytic function.]

23. Prove that u = x² - y² and v = -y/x² + y² are harmonic functions but not harmonic conjugates.[A.U. N/D 2014]

24. Find the analytic function z = u + iv, if u – v = x – y/ x² + 4xy + y² [A.U. A/M 2019 R-08]