Probability and complex function: Unit IV: Complex integration
Exercise 4.3 (Singularities residues residue theorem)
Problems with Answer | Complex integration
Probability and complex function: Unit IV: Complex integration : Exercise 4.3.
EXERCISE 4.3.
SINGULARITIES - RESIDUES - RESIDUE THEOREM
I.
Zeros, poles (or) singularities
1.
Find the zeros of ƒ (z) = sin z - z / z3
Ans.
no zeros
2.
Find the poles of f (z): z2 + 1 / 1 - z2
Ans.
-1, 1
3.
Find the poles of f (z) = cosec z
Ans.
± nπ, n = 0, 1, 2, ...
4.
Find the poles of f (z) = cot z
Ans.
± nπ, n = 0, 1, 2, ...
5.
Find the poles of f (z) = tanz
Ans.
± (2n+1), π/2, n = 0, 1, 2, ...
6.
Find the poles of f (z) = 1 / sin (1 / z - ɑ)
Ans.
z = ɑ + 1 / n π. n = ±1, ± 2, ...
7.
Find the poles of f (z) = z3 – 1 / z3 + 1
Ans.
– 1, 1/2 ± i √3/2
8.
Find the poles of f (z) = z / cos z
Ans.
±(2n + 1) π/2, n = 0,1,2,…
9.
Find the nature of the singularities of (a) z / sin z (b) cos z / z
Ans.
(a) z = 0 is a removable singularity, z = n π, n = 1, 2, ... are poles
(b)
z = 0 is a simple pole.
10.
Find the orders of the pole z = 0 of the following functions:
(i)
ez / z
Ans.
z = 0 is a simple pole
(i)
ez / z2
Ans.
z = 0 is a pole of order 2
(iii) 1- sin z / z3
Ans.
z = 0 is a pole of order 3.
11.
Find the nature of the singularities of z2/ (z - 1)2 (z -
2)
Ans.
z = 1 is a double pole and z = 2 is a simple pole
12.
Find the nature of the singularity of f (z) = (z − 3) sin (1/ z + 2)
Ans. z = -2 is an essential singularity
13.
Classify the singularity of the function f (z) = z – 1 / z2 sin (1/z
– 3)
Ans.
z = 1 is a simple zero and z = 0 is a pole of order 2
14.
Find the poles of f (z) = cot π z / (z – 1)3
Ans.
z = 1 / n π + 1, n = 0,1,2, … and z = ɑ is a pole of order 3
15.
Find the poles of f (z) = cosec z / (z - 1)3
Ans.
z = n π, n = 0, ±1, ±2, ... and z = 1 is a pole of order 3
II.
Residue
1.
Calculate the residue of z + 1 / z2 – 2z at its poles.
Ans
: -1 / 2, 3 / 2
2.
Find the residue of f (z): ez / z2 (z2 + ɑ)
Ans.
1/9 – [sin 3 + i cos 3 / 54]
3.
Find the residue of 1 / (z2 +
ɑ2) 2 at z = ɑ i
Ans.
–i / 4 ɑ3
4.
Find the residue of zez / (z
- 1)3 at its poles.
Ans.
3e / 2
5.
Find the residue of f (z) = z2 / z2 ɑ2 at its
singularities.
Ans.
- iɑ / 2 , iɑ / 2
6.
Find the residues of f (z) = z4 / (z – 1)4 ( z – 2) ( z –
3) at its singularities.
Ans
: -16, 81/16, 175/16
7.
Find the residue of f (z) = 1 / ( 1 + z2)4 at z = i
Ans.
– 5i / 32
8.
Find the residue of f (z) = z sin z / (z – π)3 at its singularity.
Ans.
residue at z = π is -1
9.
Determine the poles and residues at each of the function
f(z)
= z2 / (z − 1)3 (z
+ 2)
Ans
: 4/9 , 4/27
10.
Find the residue of f (z) = z2 sin (1/z) at z = 0
Ans.
-1 / 6
11.
Calculate the residues of f (z) = z3 - 2z / (z + 1)2 (z2
+ 4)
Ans.
7 / 25 , -3 / -3 + 4 4i , 3 / 3 + 4i
12.
Determine the poles of the following functions and the residue at each pole.
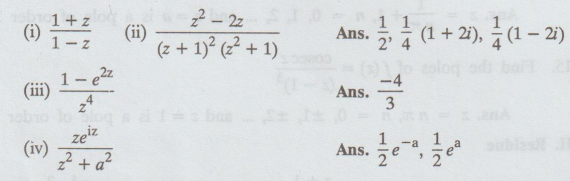
III.
Cauchy's residue theorem
1.
Determine the poles of the function f(z) = z2 / (z – 1)2 (z + 2) and residue at
each pole. Hence, evaluate 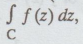 where C is the circle |z| = 2.5.
where C is the circle |z| = 2.5.
Ans
: 2πi
2.
Evaluate 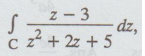 where C is the
circle
where C is the
circle
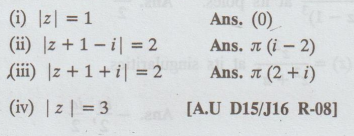
3.
Evaluate the following integral
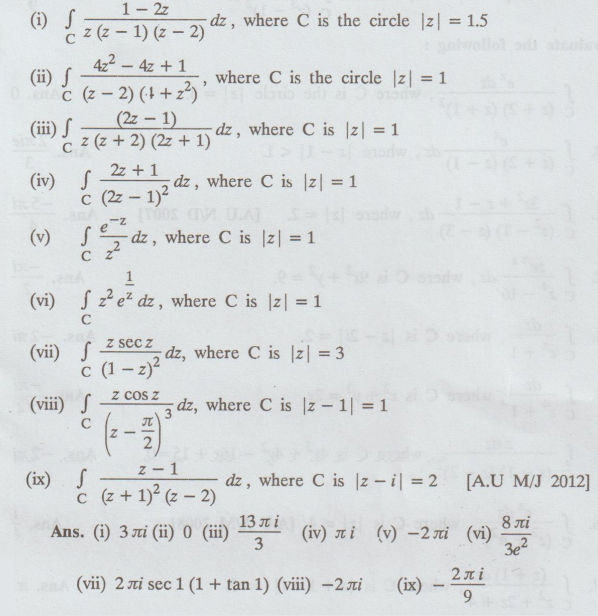
4.
Obtain Laurent's expansion for the function f(z) = 1 / z2 sinh z and
evaluate 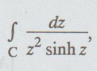 where C is the circle |z - 1| = 2
where C is the circle |z - 1| = 2
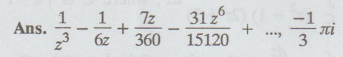
5.
If C is the circle |z|= 2 evaluate, using residue theorem

Ans
: 10 πi
6.
If C is the circle |z - i|= 2 evaluate 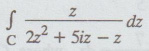
Ans.
– πi / 3
7.
Evaluate 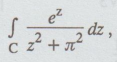 where C is |z - i| = 3.
where C is |z - i| = 3.
Ans.
-1
8.
If C is ❘z – 1 | = 1, evaluate 
Ans
: -4 πi / 9
Evaluate
the following:
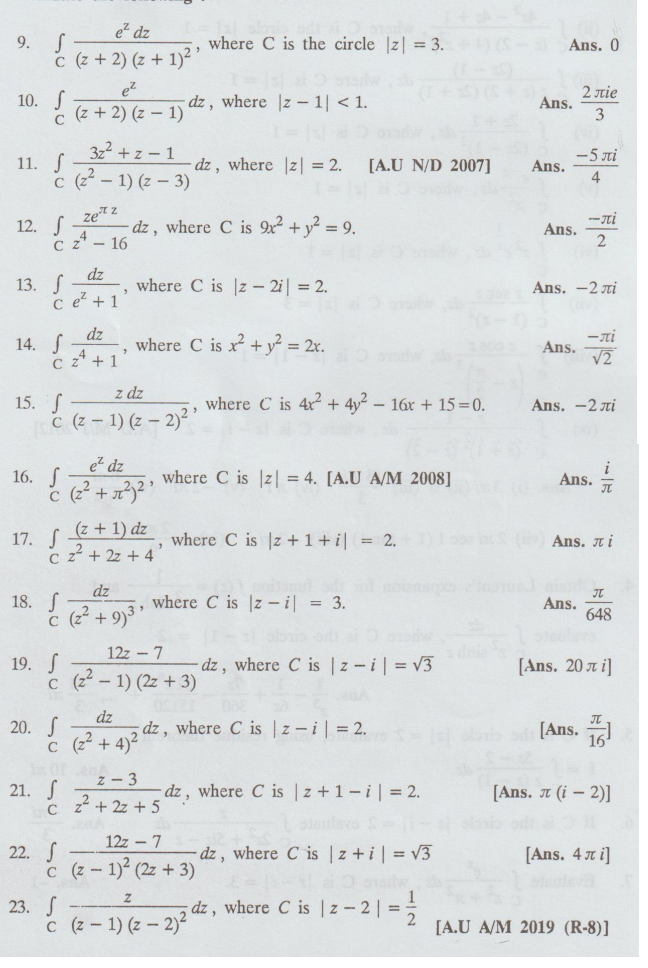
Probability and complex function: Unit IV: Complex integration : Tag: : Problems with Answer | Complex integration - Exercise 4.3 (Singularities residues residue theorem)
Related Topics
Related Subjects
Probability and complex function
MA3303 3rd Semester EEE Dept | 2021 Regulation | 3rd Semester EEE Dept 2021 Regulation
