Exercises 1.1 (Axioms of probability)

EXERCISES 1.1

1. State the axioms of probability

2. Define mutually exclusive events with an example.

3. Out of 50 students in a class, what is the probability of a single student to opt for a picnic.

[Ans. 0.02]

4. What is the probability of obtained two heads in two throws of a single coin?

[Ans. 1/4]

5. What is the probability of picking an ace and a king from a deck of 52 cards ?

 [Ans. 8/663]

6. From a bag containing 3 red and 2 black balls, 2 balls are drawn at random. Find the probability that they are of the same colour.

[Ans. 2/5]

7. Prove that the probability of an impossible event is zero.

8. When A and B are 2 mutually exclusive events such that

 P(A) = 1/2 and P(B) = 1/3, find P(A ∪ B) and P(A ∩ B).

 [Ans. P(A ∪ B) = 5/6, P(A ∩ B) = 0]

9. A fair coin is tossed 5 times what is the probability of having atleast one head?

[Ans. 31/32]

10. A card is drawn at random from a well shuffled pack, what is the probability that it is a heart or a queen.

 [Ans. 2/13]

11. Given that P(A) = 0.31, P(B) = 0.47, A and B are mutually exclusive. Then find 

[Ans. 0.31]

12. If P(A) = 0.35, P(B) = 0.73 and P(A ∩ B) = 0.14 find 

 [Ans. 0.86]

13. A card is drawn from a well shuffled pack of 52 cards. What is the probability that it is either clever or king.

[Ans. 4/13]

14. If BCA, prove that

15. Given P(A) = 1/3, P(B) = 1/4, P(A ∩ B) = 1/6, find the following probability

16. If A and B are two independent events then

17. It is given that P(A ∪ B) = 5/8, P(A ∩ B) = 1/3 and  Show that the events A and B are independent.

18. Given P(A) = 0.35, P(B) = 0.73 and P(AB) find (a) P(A ∩ B) = 0.14,

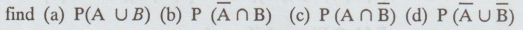
19. Given P(A) = 0.3, P(B) = 0.5 and P(A ∩ B) = 0.24 find