Exercises 1.6 (Moments - moment generating functions)

EXERCISES 1.6

1. Define m.g.f. of a discrete and continuous r.v. X.

2. Define cumulants and obtain the first four cumulants interms of central moments.

3. Define the characteristic function of a r.v. X. Show that the characteristic function of the sum of two independent variables is equal to the product of their characteristic function.

4. Find the characteristic function of r.v. X defined as

[Ans. e^{(it - 1)}/ it]

5. State any two properties of the characteristic function of a r.v. X.

6. Find the characteristic function whose probability density function is

f(x) = λ /π (λ² + x²) [Ans. e^-λ/t]

7.Show that the 7th moment for the distribution f (x) = ce^-cx, c is positive and 0 ≤ x ≤ ∞ is (r− 1)!.

8. Find the density function of the distribution for which the characteristic function is given by ϕ(t) = e –σ² t^2/2 

[Ans. 1/σ √ 2π . e.x^{-2/C2 σ 2} -∞ < x < ∞]

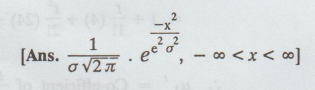
9. If the m.g.f of a R.V. 'X' is 2/ 2 - t, then find the S.D of X. [Ans. 1/2]

10. Find the m.g.f of a r.v. X whose density function is given by

f(x) = λe ^{-λ (x − a)}, x ≥ a. Hence find its mean and variance. 

[Ans. m.g.f =λ e^at/λ – t ; Mean = aλ + 1/λ ; Var = 1/λ² ]

11. The random variable X assumes the value x with the probability P (X = x) = q^x-1 p, x = 1,2,3,... Find the m.g.f of X and find its mean and variance. 

[ Ans. Pe^t/1-  e^t , 1/p , q/p² ]

12. Find the m.g.f for the given distribution

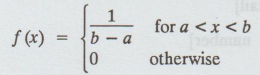
Also, find μ₁' and μ₂'' by two different methods.

[Ans. e^bt - e^at / t(b – a ) , a + b/2 , b³ - a³ / 3(b - a) ]

13. A random variable X has the p.d.f.

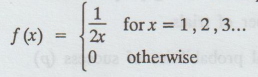
Find its m.g.f mean and variance.

[Ans. e^t / 2 – e ,2 , 2 ]

14. Give the significance of moments of a random variable.

15. Define n^m moment about origin for a random variable.

16. Find the moment generating function of a R.V X having the density function 

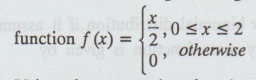
Using the generating function, find the first four moments about the origin.